Таза иілу кезіндегі кернеулер

Таза иілу кезінде Q=0, M=const. M әсерінен сырық майысады. Біртекті сырық жағдайында барлық аралықтардың қисықтығының өзгеруі бірдей болады. Сонда жазық қималар гипотезасы орындалады: сырық жүктелу алдында жазық және сырықтың деформациялан-баған өсіне перпендикуляр болған көлденең қималар сырық жүктелгеннен кейін жазық және сырықтың дефор-мацияланған өсіне перпенди-куляр болып қала береді. Сонда таза иілу кезіндегі деформация-ларды көлденең қималардың бір біріне қарағандағы бұрылудың нәтижесі ретінде қарастыруға болады (11.1 сурет). Бір-бірінен dz қашықтығында орналасқан екі қиманы қарастырайық. Оң жақтағы көлденең қимасының сол жақ қимасына карағандағы dθ бұрышына бұрылу нәтижесінде үстіңгі қабаттар ұзарады, астыңғы қабаттар қысқарады. Сонда ұзаруы да, қысқаруы да болмайтын бейтарап CD қабаты табылады. Сонда ρ бейтарап қабаттың қисықтық радиусы, dθ бұрышы мен dz ұзындығы арасында келесі тәуелдік орын алады dz= ρ∙dθ. dz ұзындығымен алынған кез келген AB кесіндісінің деформациясы осыған тең

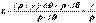. (11.1)

Гук заңы бойынша 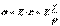(11.2)

Сонымен, таза иілу кезінде кернеулер көлденең қима бойымен сызықтық заң бойынша таралады. Бейтарап сызық (БС) дегеніміз σ=0 болатын нүктелердің геомериялық орны; ол майысқан сырық қисықтығының жазықты-ғына перепендикуляр болатыны айқын.

Таза иілу кезінде 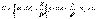болғандықтан, 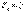болады, яғни БС көлденең қиманың ауырлық центрінен өтеді. Біз иілудің дербес жағдайын, сырықтың майысқан өсі M моментінің әсер ету жазықты-ғында жатқан жағдайын қарастырып отырмыз. Сонда

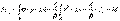, (11.3)

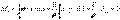. (11.4)

(11.4) теңдігінен 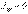болады, яғни сырық қисықтығының M жазық-тығында өзгеруі M жазықтығы қиманың бас инерция өстерінің біреуінен өтсе орын алады. Мұндай иілу тік иілу деп аталады, ал қиғаш иілу кезінде M жазықтығы мен сырық қисықтығының жазықтығы бір-бірімен түйіспейді. (11.3) теңдігінен сырық қисықтығы үшін келесі формуланы аламыз

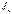. (11.5), мұнда - июші момент жазықтығына перпендикуляр, центрлік бас инерция өсіне қатысты қиманың инерция моменті. 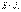шамасы сырықтың иілу кезіндегі қатаңдығы деп аталады. (11.5) теңдігін (11.2) теңдігіне қойып, σ кернеудің өрнегіне келеміз

. (11.6). Максималды кернеулер бейтарап сызықтан ең үлкен қашықтықта орналасқан нүктелерінде орын алады, олар келесіге тең (11.7). мұндағы 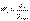- қиманың иілуге қарсыласу моменті деп аталады. Таза иілу кезіндегі беріктік шарты келесі түрде жазылады

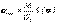(11.8). мұндағы 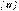- қауіпсіз кернеу.

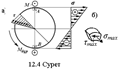
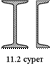
Сырықтың материалы созылу мен сығылуға бірдей қарсыласатын болмаса, беріктікке есептеуін максималды созылу және максималды сығылу кернеулері бойынша жүргізу керек екенін айтып өтейік. Көлденең қималарының ең тиімді формалары ретінде, аудандары бірдей жағдайда 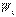қарсыласу моментінің мәндері ең үлкен болатын формалары болады - бұл, мысалы, қоставр, швеллер түріндегі прокатты стандарт профильдері (11.2 сурет).

40. Көлденең иілу кезіндегі кернеулер ж/е беріктікке есептеу.Көлденең иілу кезінде Q≠0, M=vary, сонда көлденең қималарында тек қана σ тік кернеулері емес, τ жанама кернеулері де пайда болады. τ болған кезде γ бұрыштық деформациясы да болады, сонда τ мен γ қима бойымен бірқалыпты таралмаған соң, сырықтың көлденең қималары жазық болып қала бермейді. Бірақ бұл σ мәндеріне айтарлықтай әсерін тигізбейді, сонда (11.5) пен (11.6) жеткілікті нақтылықпен орындалады деп есептеуге болады.

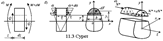Көлденең қимада b ені бойынша τ бірқалыпты таралады деп алып, оларды бейтарап сызықтан y қашықтығында орналасқан бойлық қимадағы жұптық кернеулері арқылы табуға ыңғайлы болады (11.3 сурет). Ұзындығы dz элементінен бойлық қимасымен кесіп алған бөлігі үшін тепе-теңдік теңдеулерін жазып, жанама кернеулер үшін Журавскийдің формуласын аламыз

(11.9), 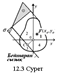мұндағы 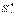- бойлық қимасынан жоғары алынған қөлденең қимасы бөлігінің x өсіне қатысты статикалық моменті.

Көптеген жағдайда τ сырықтардың беріктігіне әсерін тигізбейді (жұқа қабырғалы және қысқа сырықтардан басқасы үшін). Сонда көлденең қимасы тұрақты, созылу мен сығылуға бірдей қарсылысатын материалдан жасалған сырық үшін көлденең иілу кезіндегі беріктік шарты келесі түрде жазылады

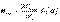(11.10)