Полный факторный эксперимент

Если в многофакторном эксперименте использованы все возможные комбинации уровней факторов, то такой эксперимент называется полным факторным экспериментом. Приведем таблицу (для линейного уравнения регрессии):

Количество факторов к	Количество неизвестных коэффициентов	Количество опытов в полном факторном эксперименте	Достаточное количество для определения коэффициентов

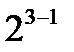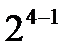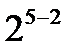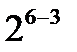Полный факторный эксперимент (ПФЭ) включает в себя 2k опытов, которые при построении линейной модели могут полностью не использоваться. В общем случае ПФЭ позволяет найти 2k коэффициентов регрессии при 2k базисных функциях. Первые k+1 базисные функции очевидны – они составляют линейную модель ( ).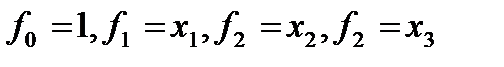

Приведем пример полного трехфакторного эксперимента (столбцы с первого по четвертый – первый столбец вводится искусственным путем и постоянен и равен 1). Эта матрица является матрицей базисных функций.

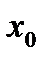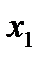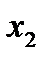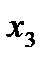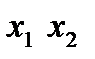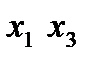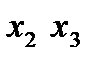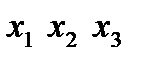	+1	-1	-1	-1	+1	+1	+1	-1
	+1	+1	-1	-1	-1	-1	+1	+1
	+1	-1	+1	-1	-1	+1	-1	+1
	+1	+1	+1	-1	+1	-1	-1	-1
	+1	-1	-1	+1	+1	-1	-1	+1
	+1	+1	-1	+1	-1	+1	-1	-1
	+1	-1	+1	+1	-1	-1	+1	-1
	+1	+1	+1	+1	+1	+1	+1	+1

Свойства полного факторного эксперимента

Матрица планирования ПФЭ обладает рядом свойств:

1) симметричность плана относительно центра эксперимента –

,

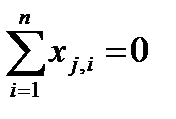то есть сумма значений уровней любого фактора (столбца) равна 0 ;

2) нормировка плана –

,

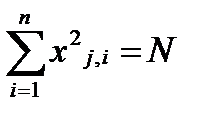сумма квадратов значений уровней любого фактора равна N (числу строк

матрицы планирования ПФЭ);

3) ортогональность плана –

,

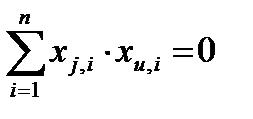сумма по парных произведений значений уровней любых 2 факторов (кроме j=u) равна 0;

4) рототабельность плана –точность предсказания значений функции отклика одинакова на равном расстоянии от центра и не зависит от направления обхода.

Свойства ортогональности и рототабельности взаимоисключающие.

Дробный факторный эксперимент

В некоторых случаях нет необходимости использовать полный факторный эксперимент. В таких случаях усекают количество строк матрицы ПФЭ до количества коэффициентов регрессионной модели. Это производится в случаях линейной регрессионной модели. Дробный факторный эксперимент удовлетворяет всем свойствам полного факторного эксперимента.

Определение коэффициентов уравнения регрессии

После проведения опытов во всех точках факторного пространства необходимо найти коэффициенты уравнения регрессии. Для этого воспользуемся методом наименьших квадратов.

;

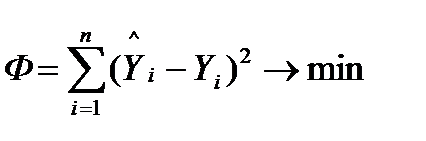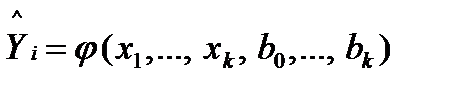
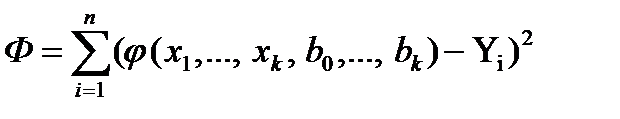, поскольку ,

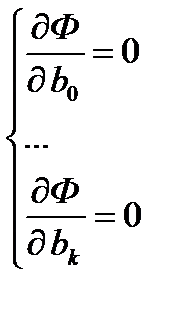то после дифференциации получим

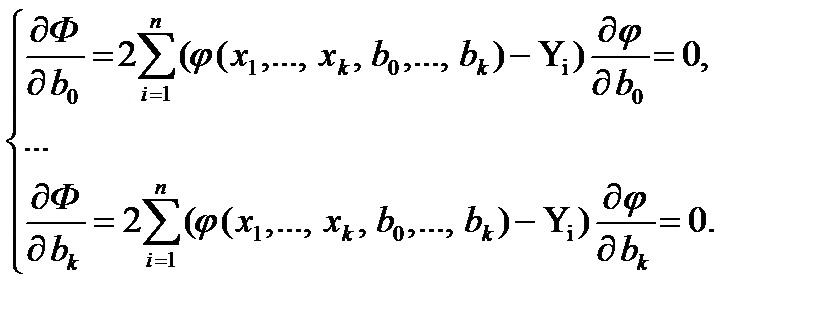
Для линейной регрессии при k=2:

.

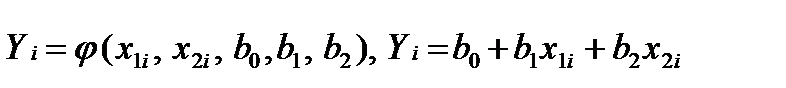Продифференцировав по коєффициентам, получим:

.

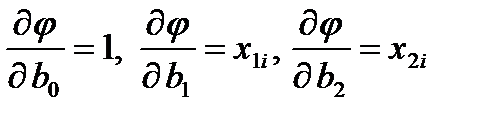Запишем уравнение в погной форме:

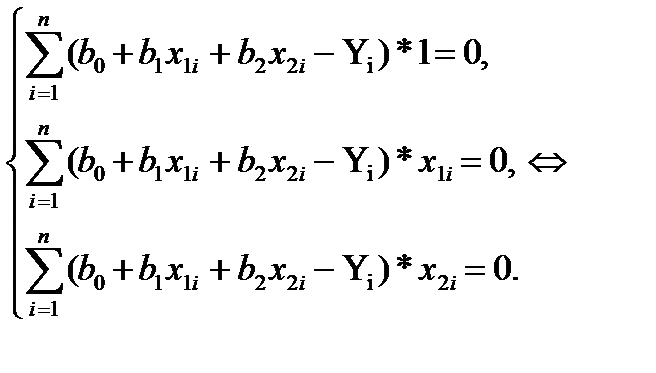
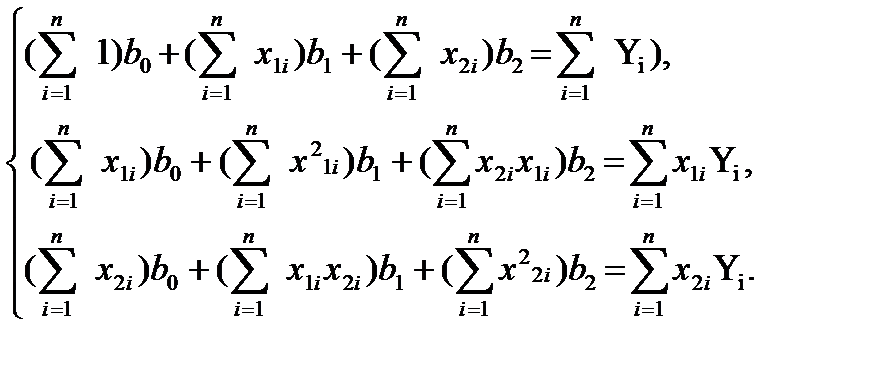
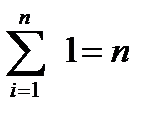, разделим каждое уравнение на n

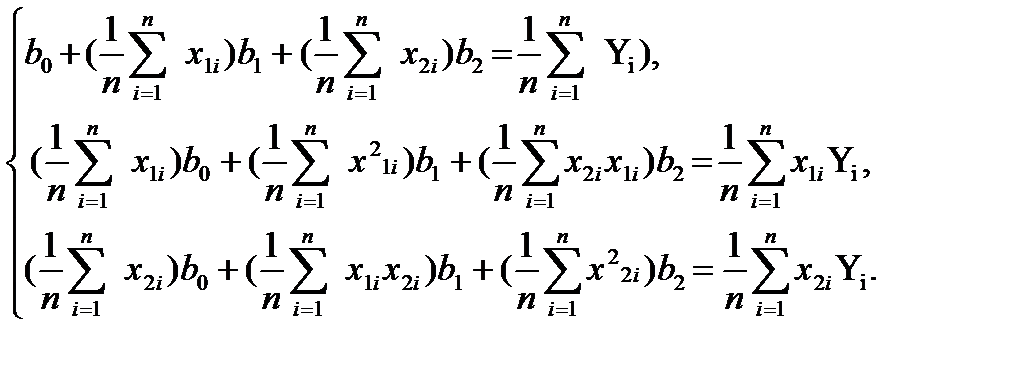
Отсюда, принимая в расчет свойства матрицы планирования, получим следующие формулы для вычисления коэффициентов

,

,

.
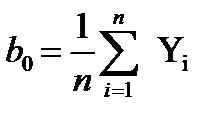
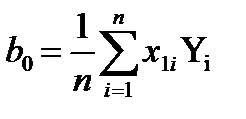
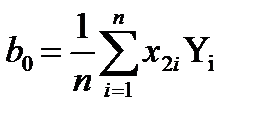