Оценка погрешности косвенных измерений

Методические указания к лабораторной работе №2

Липецк – 2014

Бурков В.Ю. Методические указания к выполнению лабораторной работы «Оценка погрешности косвенных измерений» по курсу «Метрология, стандартизация и сертификация». / В.Ю. Бурков. Липецк: ЛГТУ, 2014. – 11 с.

Предназначены для студентов технических непрофильных специальностей.

ã В.Ю. Бурков

ã Липецкий государственный технический университет, 2014

Цель работы: Изучить основ­ные принципы оценки погрешностей в ходе обработки результа­тов косвенных измерений.

Используемые приборы: Прибор комбинированный Ц4312, магазин сопротивлений Р33, Линейный источник питания Mastech HY3002.

Задание:Определить значение напряжения и силы тока, используя косвенный метод измерения. Оценить погрешность измерения

Теория к лабораторной работе:

Косвенные измерения применяются в тех случаях, когда искомое значение физической величины (ФВ) трудно получить при помощи прямого измерения.

Что бы найти искомое значение ФВ, необходимо определить другие значения ФВ, с которыми она связана определенным соотношением. Затем, используя известные физические законы и математические фор­мулы, вычисляется нужная величина. Например, измерения плотности тел, ускорения свободного падения и т.д. Однако иногда весь этот процесс происходит внутри средства измерения, и оператор измерения получает готовый результат за одно измерение. Но даже в этом случае метод измерения является косвенным.

Так как любые прямые измерения производится с некоторой степенью точ­ности, то результат косвенного измерения будет иметь некоторую неопределенность, то есть результат измерения будет выглядеть следующим образом:

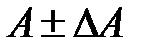, (1)

где A = ƒ(X, Y, Z,…) – значение искомой ФВ, рассчитанное на основе связанных с ней значений физических величин X , Y, Z,определяемых в ходе прямых измерений;

∆A – абсолютная погрешность косвенного измерения, которая зависит от максимальной погрешности измеренных значений X, Y, Z.

Иногда вместо абсолютной погрешности, для выражения неопределенности результата измерения используют относительную погрешность. Она определяется как процентное отношение абсолютной погрешности измерения и результат измерения, то есть:

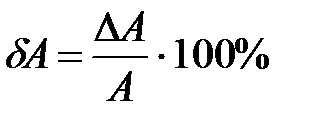. (2)

Поскольку искомое значение А определяется некоторым соотношением величин X, Y, Z, то и значение погрешности косвенного измерения определяется тем же самым соотношением через значения неопределенностей исходных ФВ ∆X, ∆Y, ∆Z. То есть результат косвенного измерения можно записать как:

ƒ(X, Y, Z,…) ± ƒ(∆X, ∆Y,∆Z,…). (3)

Рассмотрим простейшие примеры:

1. Пусть искомое значение ФВ определяется как:

X = A + B.

Тогда результат измерения будет иметь вид:

X ± ∆X = (A ± ∆А) + (B ± ∆В).

При этом значение относительной погрешности будет равно:

.

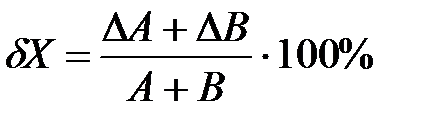Стоит отметить, что выражение в знаменателе ∆A + ∆B представляет собой случай, при котором абсолютная погрешность измерения максимальна.

2. Пусть искомое значение ФВ определяется как:

X = A ∙ B.

Тогда результат измерения будет иметь вид:

X ± ∆X = (A ± ∆А) ∙ (B ± ∆В).

X ± ∆X = (A∙B) ± (A∙∆В) ± (∆А∙B) ± (∆А∙∆В).

При этом, если минимизировать величину (∆А∙∆В) значение относительной погрешности будет равно:

;

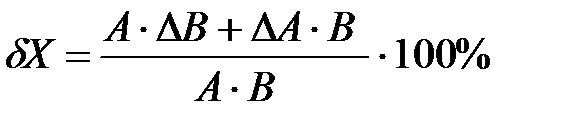или:

.

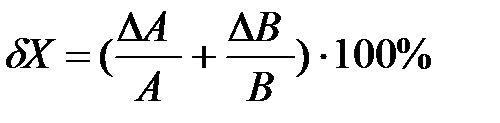3. Рассмотрим более сложный случай:

,

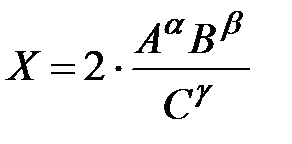где А, В, С – измеряемые физические величины;

α, β, γ – показатели степени, которые являются любыми целыми или дробными числами.

Тогда результат измерения будет иметь вид:

.

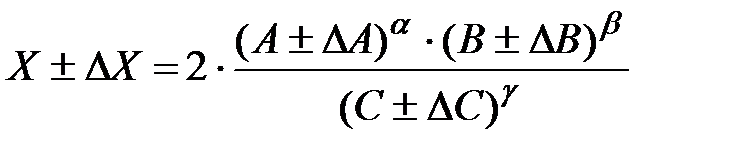При этом, используя формулу для раскрытия степенного многочлена, значение относительной погрешности будет равно:

.

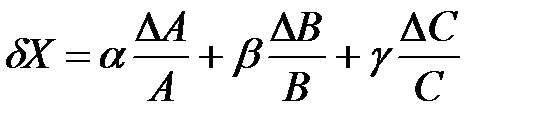Стоит отметить, что в данном выражении присутствуют члены 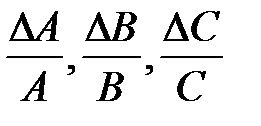. Подобные члены выражения уже встречались в примере 2. Так же можно справедливо заметить, что выражения для расчета относительной погрешности намного проще, чем выражения для расчета абсолютной погрешности. Поэтому, имеет смысл при косвенных измерениях сначала определять относительную погрешность.

Однако есть одно замечание. Приведенные формулы могут применяться только в том случае, если параметры результата косвенного измерения не зависят друг от друга. В противном случае будет возникать ошибка в расчетах.

Для исключения таких ситуаций нужно использовать дифференциальное исчисление.

Пусть имеется некоторая функция описывающая косвенное измерение:

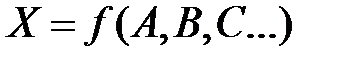. (4)

Относительную погрешность косвенного измерения можно определить как:

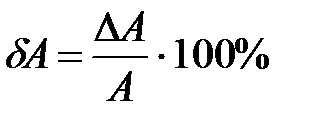или .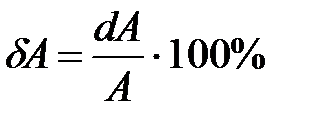

Данное выражение можно записать как:

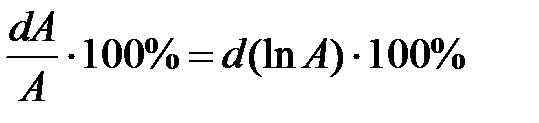
Для нахождения относительной погрешности необходимо:

1. Прологарифмировать исходную формулу ln A = ln ƒ(X, Y, Z, …)

2. Продифференцировать полученное уравнение, заменив затем дифференциалы dA, dX, dY погрешностями ΔA , ΔX , ΔY ;

3. Сгруппировать члены, содержащие одни и те же погрешности, вынести эти погрешности за скобки, а выражения в скобках взять по модулю;

4. Заменить знаки « - » перед коэффициентами при погрешностях на знак « + » (для нахождения максимального значения).

Таким образом, общая формула для расчета относительной погрешности будет при этом выглядеть следующим образом:

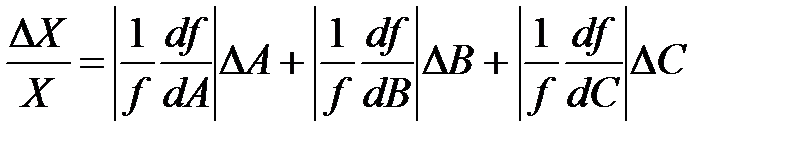(5)

Порядок выполнения работы:

1. Определить предельно допустимые погрешности магазина сопротивления Р33 и комбинированного прибора Ц4312 формуле:

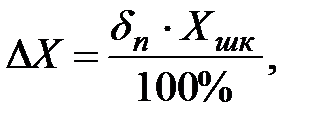
где Х_шк – длина шкалы;

d_п – нормирующий показатель(класс точности).

2. Собрать установку по заданной схеме.

3. Для двух заданных пределов измерения определить цену деления шкалы по формуле:

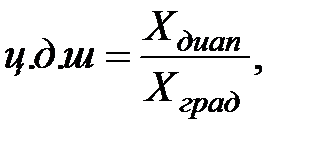
где Х_диап – длина шкалы согласно выбранному диапазону;

Х_град – длина шкалы согласно градуировке.

4. Для каждого предела измерения произвести одну серию из пяти косвенных измерений, регулируя напряжение в схеме с помощью магазина сопротивления так, чтобы значения показаний напряжения на комбинированном приборе Ц4312 строго соответствовали делениям шкалы. При этом значения напряжения не должны быть расположены близко друг к другу.

5. Рассчитать значение электрического тока в схеме для каждого измерения по формуле:

.

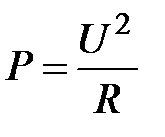6. Найти оценку погрешности измерения по формуле 5 для каждого измерения.

7. Записать результат измерения, построить графики зависимости ∆P от P и сделать вывод по проделанной работе.

Контрольные вопросы:

1. Дать определение абсолютной погрешности измерения.

2. Дать определение относительной погрешности измерения.

3. Чем отличаются прямые и косвенные измерения?

4. Как определить погрешность измерения исходя из класса точности средства измерения?

5. Как определить цену деления шкалы измерительного прибора?