Общая характеристика тепловых процессов

Лекция 8

ОСНОВЫ ТЕПЛОПЕРЕНОСА

ОБЩАЯ ХАРАКТЕРИСТИКА ТЕПЛОВЫХ ПРОЦЕССОВ

Технологические процессы, скорость протекания которых определяется скоростью подвода или отвода тепла, называют тепловыми, а аппараты, предназначенные для проведения этих процессов теплообменными.

К тепловым процессам относятся нагревание, охлаждение, конденсация, испарение.

Нагревание повышение температуры перерабатываемых материалов путем подвода к ним тепла.

Охлаждение понижение температуры перерабатываемых материалов путем отвода от них тепла.

Конденсация сжижение паров какого-либо вещества путем отвода от них тепла.

Испарение перевод в парообразное состояние какой-либо жидкости путем подвода к ней тепла.

Частным случаем испарения является выпаривание -концентрирование при кипении р-ров твердых нелетучих веществ путем удаления жидкого летучего растворителя в виде паров.

В тепловых процессах взаимодействуют не менее чем две среды с различными температурами; при этом тепло передается самопроизвольно (без затраты энергии) только от среды с более высокой температурой (называемой теплоносителем) к среде с более низкой температурой (называемой холодильным агентом, или хладоагентом).

В химической технике приходится осуществлять тепловые процессы при различных температурах от близких к абсолютному нулю до равных нескольким тысячам градусов. Для каждого конкретного процесса, протекающего в определенном интервале температур, подбирают наиболее подходящие теплоносители и хладоагенты, которые должны быть химически стойкими в рабочих условиях и легко транспортируемыми по трубам, не должны образовывать отложений на стенках аппаратов и вызывать коррозию аппаратуры.

Наиболее распространенные в химической технологии теплоносители и хладоагенты - гелий, водород, азот, кислород, воздух, метан, этан, этилен, фреоны, хладоны, аммиак, диоксиды серы и углерода, этиленгликоль, рассол хлорида кальция, вода.

Основная характеристика любого теплового процесса количество передаваемого тепла: от этой величины зависят размеры теплообменных аппаратов. Основным размером теплообменного аппарата является теплопередающая поверхность (поверхность теплообмена).

Связь между количеством передаваемого в аппарате тепла и поверхностью теплообмена определяется основным кинетическим уравнением переноса тепла. Это уравнение обычно называют основным уравнением теплопередачи:

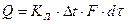, (1)

где Q-количество тепла, переданного через всю поверхность теплообмена в единицу времени; К- коэффициент теплопередачи между средами; -средняя разность температур между средами; F -поверхность теплообмена, 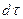-продолжительность теплообмена.

Для установившегося процесса и единицы времени основное уравнение теплопередачи имеет вид: 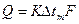(2)

Из уравнения (2) определяют поверхность теплообмена аппарата 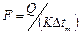(3) если известны значения величин, входящих в правую часть соотношения.

Среднюю разность температур между средами определяют по начальным в конечным температурам сред участвующих в теплообмене.

Определение коэффициента теплопередачи, являющегося коэффициентом скорости теплового процесса, представляет наибольшие трудности при расчете теплового аппарата. Коэффициент теплопередачи зависит от характера и скоростей движения теплообменивающихся сред, а также от условий, в которых протекает теплообмен.

Тепло может распространяться различными способами: теплопроводностью, конвекцией и тепловым излучением.

Теплопроводностью (кондукцией)-называют процесс распространения тепла между частицами тёла, находящимися в соприпкосновении; при этом тепловая энергия передаётся внутри тела от одних частичек к другим вследствие их колебательного движения. Процесс теплопроводности наблюдается в твердых телах и в тонких слоях жидкостей или газов.

Конвективным теплообменом (конвекцией) называют процесс переноса тепла вследствие движения и перемешивания макроскопических объемов газа или жидкости.

Тепловым излучением называют процесс распространения тепла в виде электромагнитных волн (инфракрасное излучение). В излучающем теле тепло превращается в энергию излучения, которая распространяется в пространстве. Встречая на своем пути тело, лучистая энергия частично превращается в тепло, частично отражается от этого тела и частично проходит сквозь него.

На практике в большинстве случаев тепло распространяется одновременно двумя-тремя указанными способами, т.е. происходит сложный теплообмен.

ТЕПЛОПРОВОДНОСТЬ

Распространение тепла теплопроводностью происходят при неравенстве температур внутри рассматриваемого тела (среды). Температурное поле в общем случае определяется функциональной зависимостью 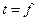(x,y,z,τ), где t-температура в рассматриваемой точке; х,у,z координаты точки; τ время.

Если температура не изменяется во времени, то температурное поле называется стационарным (установившимся), если температура изменяется во времени, то оно называется нестационарным (неустановившимся).

Геометрическое место точек, имеющих одинаковую температуру, называется изотермической поверхностью. Температуры изменяются в направлении от одной изотермической поверхности к другой. Предел отношения изменения температуры Δt к расстоянию между изотермическими поверхностями по нормали Δt называется температурным градиентом и обозначается символом grad t град/м. 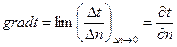(4)

Температурный градиент является векторной величиной. Положительным направлением температурного градиента принято считать направление возрастания температур (вдоль нормали к изотермической поверхности).

Закон Фурье. На основании опытного изучения процесса распространения тепла в твердых телах Фурье установил основной закон теплопроводности, который гласит, что количество тепла,переданного теплопроводностью, пропорционально градиенту температуры дt/дn, времени d 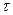и площади сечения dF, перпендикулярного направлению теплового потока, т. е.

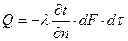. (5)

Коэффициент пропорциональности называют коэффициентом теплопроводности. Он характеризуетспособность тел проводить тепло и имеет размерность:

.

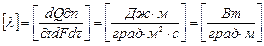λ показывает, какое количество тепла проходит вследствие теплопроводности через 1 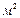поверхности в единицу времени при разности температур 1 град, приходящейся на 1м длины нормали к изотермической поверхности. Коэффициент теплопроводности веществ зависит от их природы и агрегатного состояния. Коэффициент теплопроводности: для газов 0,0050,5, для жидкостей 0,080,7, для изоляционных и строительных материалов 0,02-3,0, для металлов 2,3- 458.

Коэффициенты теплопроводности веществ зависят от температуры в давления. Для газов они возрастают с повышением температуры и мало зависят от давления; для жидкостей с увеличением температуры, как правило, уменьшаются (исключение составляют вода и глицерин). Теплопроводность твердых тел в большинстве случаев увеличивается с повышением температуры.

Дифференциальное уравнение теплопроводности. Процесс распространения тепла теплопроводностью может быть описан математически дифференциальным уравнением. Это уравнение выводят на основе закона сохранения энергии, при этом предполагают, что тепло распространяется в теле (среде), физические свойства которого -плотность ρ, теплоемкость с и теплопроводность λ-не изменяются по направлениям и во времени.

Для вывода дифференциального уравнения теплопроводности выделим в теле элементарный параллелепипед с ребрами dх, dу и dz (рис. 1). Если через этот элементарный параллелепипед тепло распространяется теплопроводностью, то через грани левую, заднюю и нижнюю за время Δτ в него входят количества тепла соответственно 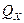, , 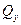, 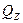а через противоположные грани - правую, переднюю и верхнюю - выходят количества тепла соответственно 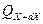, 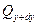и .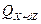

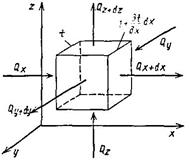
Рис. 1. К выводу дифференциального уравнения теплопроводности Фурье.

Разность между количеством тепла, введенным в параллелепипед за время dτ и выведенным из него за тот же промежуток времени, определится равенством

.

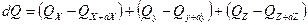Согласно закону теплопроводности Фурье,

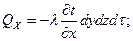
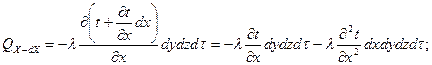
Следовательно,

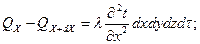
Аналогично найдем для:

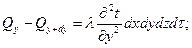
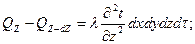
Складывая левые и правые части трех последних равенств получим:

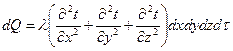(6)

На основе закона сохранения энергии разность количества тепла dQ равна кол-ву тепла, которое идет на изменение энтальпии параллелепипеда (удельной теплоемкости материала) за время dτ:

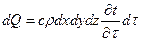(6.7)

Сопоставляя соотношения (6) и (7), получаем дифференциальное уравнение теплопроводности Фурье: 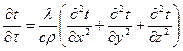(8)

В уравнении (8) множитель пропорциональности λ/(сρ) называют коэффициентом температуропроводности: .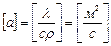

Дифференциальное уравнение теплопроводности Фурье обычно записывают в виде 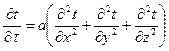(9) или 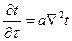(10)

Это уравнение дает возможность решать задачи, связанные с распространением тепла в теле (среде) теплопроводностью как при установившемся, так и при неустановившемся тепловом потоке. При решении конкретных задач дифференциальное уравнение дополняется начальными и граничными условиями, характеризующими каждую конкретную задачу.

В теплообменных аппаратах поверхности нагрева представляют собой плоские, цилиндрические или сферические стенки, поэтому решение задач распространения тепла теплопроводностью в телах с указанными геометрическими формами имеет большое практическое значение. Теплопроводность плоской стенки. Рассмотрим плоскую стенку толщиной δ из однородного материала, имеющего коэффициент теплопроводности λ.Температура на противоположных наружных поверхностях стенки равна 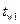и 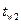, причем > .

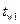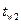Для вывода уравнения теплопроводности плоской стенки воспользуемся дифференциальным уравнением Фурье (9).

При установившемся тепловом режиме температура в различных точках стенки не изменяется во времени, т. е. 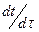=0.

Температурное поле одномерно, т.е. температура изменяется только по одному направлению (вдоль оси х) .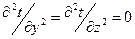

Таким образом, для плоской стенки при установившемся тепловом режиме уравнение (9) записывается 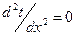. (11)

В результате интегрирования уравнения получим:

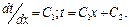
Постоянные интегрирования и 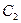находим из условий на границе (х=0 и х=δ):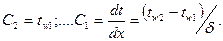

В результате получим:

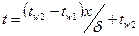(12)

т.е. температура по толщине плоской стенки при установившемся тепловом режиме изменяется линейно, а температурный градиент сохраняет постоянное значение.

Подставив найденное значение температурного градиента в уравнение (5), выражающее основной закон теплопроводности, получим уравнение теплопроводности плоской стенки при установившемся тепловом режиме:

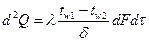или 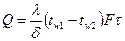. (13)

Отношение λ/δ называют тепловой проводимостью стенки, а обратную ему величину δ/λ тепловым, или термическим, сопротивлением стенки.

Теплопроводность многослойной стенки.

Стенки теплообменной аппаратуры часто состоят из нескольких слоев различных материалов, имеющих различные толщины. Уравнения теплопроводности таких сложных стенок могут быть выведены из уравнения (13).

Рассмотрим плоскую многослойную стенку, состоящую из n слоев. Толщины слоев равны 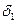, , 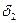, 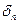а коэффициент теплопроводности материалов, из которых образованы эти слои соответственно 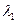, ,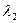…, 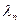.Температуры на противоположных поверхностях многослойной стенк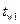и и 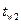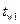> 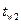, а температуры на границах между слоями , , .

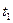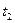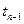При установившемся тепловом режиме количество тепла, проходящего через каждый слой, одинаково. Уравнения теплопроводности для каждого из слоев могут быть выражены соответственно уравнению (13) следующим образом:

для 1-го слоя или 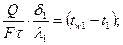для 2-го слоя 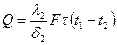или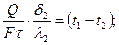

для n-го слоя 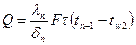или .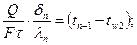

Складывая правые и левые части этих уравнений, получаем уравнение теплопроводности плоской многослойной стенки при установившемся тепловом режиме:

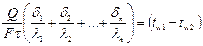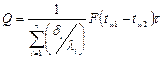или .(14)

Где i- порядковый номер слоя; n - число слоев.

Как видно из уравнения (14), общее термическое сопротивление плоской многослойной стенки равно сумме термических сопротивлений слоев.