Влияние структуры и суммарного коэффициента системы на устойчивость

Существуют САУ, которые неустойчивы при любых значениях параметров. Такие системы называют структурно неустойчивыми. Структурно неустойчивую систему можно сделать устойчивой, изменив ее структуру.

Рассмотрим в качестве примера одноконтурную систему, содержащую одно апериодическое звено и два интегрирующих звена. Характеристическое уравнение такой системы имеет вид

(T2× p + 1) × p2 + K = 0 (4.22)

и не содержит слагаемое с p в первой степени, т.е. a1=0. Очевидно, что в данном случае не выполняется необходимое условие устойчивости - условие положительности коэффициентов характеристического уравнения, и никакие вариации параметров T2 и K не могут привести к появлению слагаемого с p в первой степени. Следовательно, эта система структурно неустойчива.

Существуют звенья, которые, как правило, ухудшают устойчивость системы, и звенья, которые почти всегда улучшают устойчивость. К первой группе относятся звенья:

интегрирующее

W(p) = 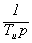; (4.23)

неустойчивое инерционное звено первого порядка

W(p) = 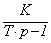; (4.24)

консервативное

W(p) = 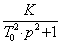. (4.25)

Звеньями, улучшающими устойчивость системы, являются форсирующие звенья. Обычно используют форсирующие звенья первого порядка

W(p) = T_ф× p + 1. (4.26)

Рассмотрим общие условия структурной устойчивости одноконтурной системы. Характеристическое уравнение замкнутой системы в общем случае имеет вид

Dз(p) = Dp(p) + Mp(p) = 0,

где Dp(p)= 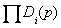- произведение знаменателей передаточной функции отдельных звеньев, входящих в контур системы;

Mp(p) - произведение числителей этих же функций.

Условия структурной устойчивости зависят от порядка п характеристического уравнения и вида многочленов Dp(p) и Mp(p). Обозначим:

n- число интегрирующих звеньев (4.23);

t - число неустойчивых звеньев;

r - число консервативных звеньев, входящих в систему.

Если форсирующих звеньев в контуре нет, т.е. Mp(p)=К (где - К коэффициент усиления системы), то условие структурной устойчивости системы выражается в виде двух неравенств:

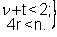(4.27)

Для более сложных видов многочлена Mp(p) условия структурной устойчивости одноконтурных систем приводятся в специальной литературе.

Рассмотрим влияние одного из основных параметров системы - суммарного коэффициента усиления разомкнутого контура на ее устойчивость. Учтем, что для одноконтурных систем коэффициент К входит в выражение ЧПФ W(jw) как множитель

W(jw) = 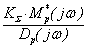, (4.28)

где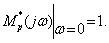

Это означает, что длины вектора W(jw) при всех значениях w пропорциональны коэффициенту К.

При увеличении коэффициента К АФХ расширяется (рис. 4.7,а) и приближается к критической точке (-1, j0). Следовательно, увеличение добротности системы приводит к нарушению устойчивости системы.

Это правило справедливо для большинства реальных систем, т.е. систем с АФХ первого рода. Однако существуют системы с АФХ второго рода (рис. 4.7,б). В таких системах к нарушению устойчивости может привести не только увеличение, но и уменьшение коэффициента усиления.

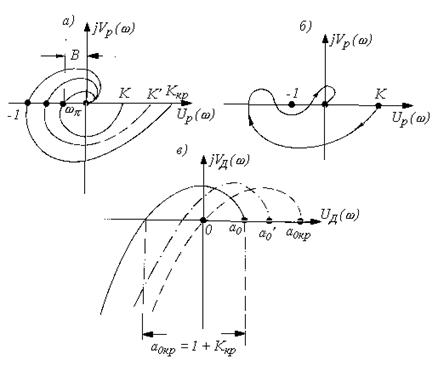
Рис 4.7. Определение предельного значения коэффициента усиления

Значение коэффициента усиления, при котором АФХ разомкнутой системы проходит через точку (-1, j 0), т.е. при котором замкнутая система находится на границе колебательной устойчивости, называют предельным иликритическим. Этот вопрос с помощью критерия Гурвица рассматривался в 4.2 (см. пример 4.1).

Если Ap(wp) = çWp(jwp)ç = B (см. рис. 4.7,а), Ккр = К/В.

Таким образом, установлена одна из важнейших в ТАУ закономерностей

чем больше суммарный коэффициент усиления разомкнутого контура регулирования, тем ближе замкнутая система к границе устойчивости.

Предельное значение коэффициента усиления зависит от соотношения постоянных времени звеньев, образующих контур системы. Рассмотрим систему, структурная схема которой показана на рис. 4.8.

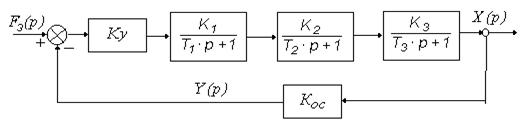
Рис. 4.8

Передаточная функция замкнутой системы

Wз(jw) = 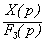= 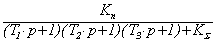, (4.29)

где K_S = KуK1K2K3 Kос

D(p) = a3× p3 + a2× p2 + a1× p + a0 ,

где

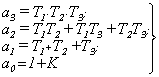(4.30)

Согласно критерию Гурвица система третьего порядка будет находиться на границе колебательной устойчивости при

D2 = а1а2 - а0а3 = 0. (4.31)

Подставив в уравнение (4.31) коэффициенты (4.30), получим

(Т1Т2 + Т1Т3 + Т2Т3)( Т1 + Т2 + Т3) - Т1Т2Т3(1 + ККР) = 0. (4.32)

Решив это равенство относительно ККР и выполнив некоторые дополнительные преобразования (деление на а3), получим

ККР = 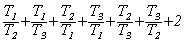. (4.33)

На основании выражения (4.33) можно сформулировать важное практическое правило:

предельное значение добротности системы зависит от соотношения постоянных времени и не зависит от их абсолютных значений.

В рассматриваемом случае ККРмин=8 при Т1=Т2=Т3.

Для увеличения ККР целесообразно уменьшать наименьшую постоянную времени.

Рассмотрим случай контура регулирования, состоящего из п одинаковых апериодических звеньев с Тi=Т. Для нахождения ККР используем условия прохождения АФХ разомкнутого контура через точку (-1;j 0). В этом случае частота среза wс=wp, что позволяет записать следующие два уравнения:

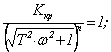(4.34)

n× arg tg(wс× T) = - p. (4.35)

Из уравнения (4.35) получаем

wс× T = - tg(p/n). (4.36)

Подставив (4.36) в уравнение (4.34), найдем

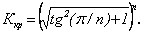(4.37)