Задача 1. Анализ одномерных случайных данных

Часть 1. СТАТИСТИЧЕСКИЙ АНАЛИЗ СЛУЧАЙНЫХ ВЕЛИЧИН

Сформировать исходные данные

Исходным материалом для статистического исследования служит: совокупность из N наблюдений, которая может быть извлечена из еще большей совокупности, называемой генеральной.

N = 1000

Выбрать из генеральной совокупности выборку

Основой любых выводов о вероятностных свойствах генеральной совокупности X, т.е. статистических выводов, является выборочный метод, суть которого заключается в том, что свойства случайной величины X устанавливаются путем изучения тех же свойств на случайной выборке и генеральной совокупности.

n = 100

Назначить для выборки анализируемый признак

Исследуемый признак Х

Записать выборку (по назначенному признаку) в (произвольной последовательности) последовательности значений

Каждое значение исследуемой величины х_i (n = 1 … n) Значения х_i называются вариантами

Пример. Имеется выборка значений механической скорости бурения v_м коронкой И4ДП-59 в трещиноватых и абразивных породах X — XI категорий по буримости:

0,67	0,70	0,75	0,72	0,71	0,80	0,78	0,77	0,71	0,74
0,78	0,68	0,85	0,74	0,77	0,71	0,77	0,72	0,84	0,76
0,74	0,76	0,80	0,75	0,74	0,74	0,81	0,79	0,75	0,71
0,69	0,76	0,79	0,73	0,78	0,73	0,75	0,76	0,77	0,75
0,70	0,82	0,85	0,80	0,72	0,77	0,79	0,83	0,77	0,75
0,82	0,71	0,85	0,78	0,75	0,75	0,73	0,72	0,73	0,75
0,76	0,74	0,76	0,76	0,78	0,84	0,75	0,74	0,73	0,82
0,69	0,81	0,81	0,76	0,78	0,72	0,71	0,83	0,73	0,77

Построить вариационный ряд

Последовательность, записанная в возрастающем порядке — вариационным рядом Вариационным рядом для этой выборки служит последовательность значений механической скорости бурения, м/час:

0,67	0,73	0,76	0,78
0,68	0,73	0,76	0,79
0,69	0,73	0,76	0,79
0,69	0,74	0,76	0,79
0,70	0,74	0,76	0,80
0,70	0,74	0,76	0,80
0,71	0,74	0,76	0,80
0,71	0,74	0,76	0,81
0,71	0,74	0,77	0,81
0,71	0,74	0,77	0,81
0,71	0,75	0,77	0,82
0,71	0,75	0,77	0,82
0,72	0,75	0,77	0,82
0,72	0,75	0,77	0,83
0,72	0,75	0,77	0,83
0,72	0,75	0,78	0,84
0,72	0,75	0,78	0,84
0,73	0,75	0,78	0,85
0,73	0,75	0,78	0,85
0,73	0,75	0,78	0,85

Вычислить характеристики вариационного ряда

Объем выборки 80 значений. Минимальное значение вариационного ряда x_min = ___ . Максимальное значение ряда x_max = ____. Размах выборки R = x_max - x_min = ______.

Построить группированный статистический ряд

Статистическим рядом (распределением) выборки - перечень вариант и соответствующих им частот или относительных частот. Статистический ряд с абсолютными частотами для исходной выборки:

y_i	-3	-2	-1	0	1	2
n_i	1	1	3	2	2	1

Статистический ряд с относительными частотами

y_i	-3	-2	-1	0	1	2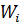
	0,1	0,1	0,3	0,2	0,2	0,1

Статистический группированный ряд

Механическая скорость бурения, х_i м/ч	0,67	0,68	0,69	0,70	0,71	0,72	0,73	0,74
Абсолютная частота совпадений значений СВ, n_i	1	1	2	2	6	5	6	7

x_i, м/ч	0,75	0,76	0,77	0,78	0,79	0,80	0,81	0,82
n_i	10	8	7	6	3	3	3	3

x_i, м/ч	0,83	0,84	0,85
n_i	2	2	3

Построить интервальный статистический ряд

Группированный статистический ряд - совокупность середин интервалов z_k = (x_k+x_k₊₁)/2 и соответствующих им частот n_k. Группированный статистический ряд используется преимущественно при анализе вида распределения случайных величин по данным наблюдений.

Выбрать число интервалов

Выбор числа интервалов зависит от размаха и объема выборки Число интервалов группировки выбирается произвольно, обычно не менее пяти и не более 15 Число интервалов при n = 200-300 и более ряд авторов рекомендуют брать в пределах от 10 до 20 Следует учитывать, что при большом числе интервалов картина распределения искажается случайными зигзагами частот, при слишком малом характерные особенности распределения получается слишком сглаженной Для построения группированного ряда принято t = ______ интервалов. Ширина интервалов оправляются по формуле: r_t = R/t + Δ_t,

Вычислить границы интервалов

Границы определяются так: Значение левой границы + ширина интервала Значения границ интервалов

Номер интервала, t	Значение левой границе интервала	Значение правой границе интервала

Построить таблицу с группированным рядом

Среднее значение xi определяется как среднее арифметическое значений случайной величины, попавших в интервал Группированный статистический ряд

Номер интервала	Границы интервалов	Среднее значение xi	Частоты попадания в интервал	Накопленная частота

Определитьотносительные частоты (частости)

Числа n_i называются частотами, Отношения частот к объему выборки n называются относительными частотами W_i W_i = n_i/n (1) Группированный статистический ряд

Номер интервала	Границы интервалов	Среднее значение xi	Относительные частоты попадания в интервал

Проверить правильность определения относительных частот

Контроль: ∑W_i = 1 W = 0,1+0,2+0,25+0,3+0,15 = 1.

Построить статистические диаграммы

Для наглядности сгруппированные статистические ряды представляют графиками: гистограмма, полигон, кумулята; огива.

Построить гистограмму и полигон

Гистограмма представляет собой столбиковую диаграмму частот. По горизонтальной оси диаграммы откладывают измеренные значения из набора данных, по вертикальной – частоту встречаемости этих значений. Высота каждого столбца показывает частоту (количество) значений из набора данных, принадлежащих соответствующему интервалу, равному ширине этого столбца. Визуальный анализ гистограмм позволяет выявить характер распределения данных и ответить на следующие шесть вопросов: 1. Какие значения типичны для заданного набора данных? 2. Как различаются между собой значения (диапазон значений)? 3. Сконцентрированы ли данные вокруг некоторого типичного значения? 4. Какой характер имеет эта концентрация данных? В частности, одинаков ли характер «затухания» для малых и больших значений данных? 5. Есть ли в заданном наборе такие значения, которые сильно отличаются от остальных и требуют специальной обработки (выбросы)? 6. Можно ли сказать, что в целом это однородный набор или отчетливо наблюдается наличие групп, которые надо анализировать отдельно?

Определить накопленные частоты

Таблица 5 - Группированный статистический ряд

Номер интервала	Границы интервалов	Среднее значение xi	Частоты попадания в интервал	Накопленная частота

Наши рекомендации

Pascal. Массивовый тип данных. Организация одномерных, многомерных массивов. Записи

Задача 2. Корреляционный анализ данных

Анализ одномерных потоков при нелинейных законах фильтрации

Вопрос №62 – корреляционный анализ случайных величин и случайных процессов

Статистика i: анализ одномерных распределений

Анализ одномерных распределений.

Анализ одномерных распределений

Задача 9. На основании данных, приведенных в таблице, проведите качественный анализ процентных доходов банка, сформулируйте вывод.

Задача №3 Группировка статистических данных и анализ групп

← Предыдущая страница | Следующая страница →