Инейные дифференциальные уравнения второго порядка

Определение 4. Линейным дифференциальным уравнением второго порядка называется уравнение вида:

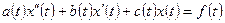, (3.16)

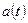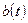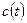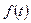где , , и - заданные функции, причем 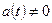. Здесь, для удобства записи использованы обозначения , .

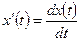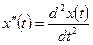Если функции 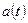, , 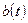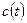постоянны, то уравнение (3.16) называют уравнением с постоянными коэффициентами.

Если 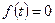при всех значениях 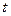, то уравнение называют однородным.

Рассмотрим однородное уравнение с постоянными коэффициентами:

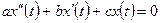, (3.17)

где 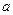, , 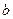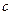- постоянные, причем .

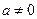Решение уравнения (3.17) будем искать в виде:

,

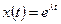где 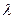- некоторое число.

Учитывая, что 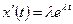, 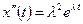из (3.17) имеем:

.

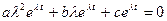Или

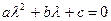. (3.18)

Уравнение (3.18) называется характеристическим уравнением для уравнения(3.17). Корнями характеристического уравнения служат

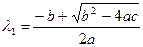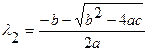, . (3.19)

Нужно рассмотреть три случая: величина 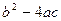больше нуля, равна нулю или меньше нуля.

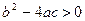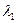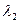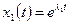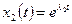Случай 1. Пусть , т.е. и действительны и различны. Тогда дифференциальное уравнение имеет два разных решения: и . Общее решение записывается в виде:

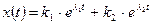, (3.20)

где 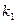и 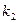- произвольные постоянные. Чтобы найт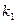и и 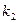нужно знать два условия, которым должно удовлетворять решение 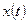, например, 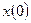и .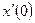

Случай 2. Пусть 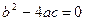. В этом случае корни характеристического уравнения равны между собой: 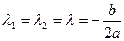. Одним решением (3.17) является функция 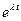, а другим 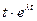. Общее решение имеет вид:

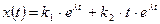. (3.21)

Случай 3. Пусть 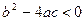. В этом случае корни характеристического уравнения (3.18) представляют собой комплексно-сопряженные числа

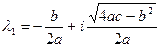и .

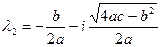Общее решение уравнения (3.17 запишется в виде:

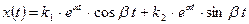, (3.22)

где , .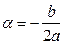

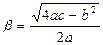Пример 9. В благоприятных условиях выращивают две популяции мух. Для популяции I удельная скорость роста составляет 0.1, если время выражается в днях. Для популяции II аналогичная скорость составляет 0.08. Определим 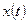как суммарную численность двух популяций в момент 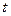. Найти дифференциальное уравнение второго порядка, которому удовлетворяет .

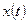Решение: По условию задачи 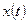- суммарная численность двух популяций мух. Учитывая, что 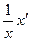- есть удельная скорость роста, то для 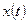имеем уравнение

.

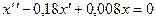Это есть дифференциальное уравнение второго порядка, которому удовлетворяет 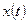. Решая, находим:

.

.

; .

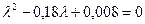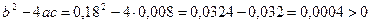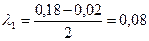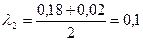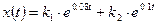- общее решение уравнения.

Упражнения

1. Согласно наблюдениям, скорость роста популяции бактерий в момент t (время выражается в часах) равна размеру популяции 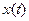, поделенному на 5. Опишите этот процесс роста дифференциальным уравнением для 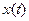. Каков порядок этого уравнения?

2. Дрожжи в растворе сахара растут таким образом, что их масса увеличивается со скоростью, равной половине массы в момент t (время выражается в часах). Опишите изменение массы дрожжей с помощью дифференциального уравнения. Каков порядок этого дифференциального уравнения?

3. Найдите общие решения для следующих уравнений первого порядка:

а)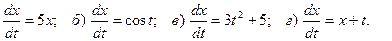

4. Для следующих уравнений первого порядка найдите решения, удовлетворяющие начальному условию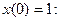

а)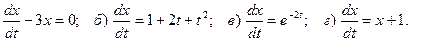

5. В эксперименте с голоданием масса испытуемого за 30 дней уменьшилась со 140 до 110 фунтов. Ежедневные потери массы, согласно наблюдениям, были пропорциональны массе испытуемого. Какому дифференциальному уравнению удовлетворяет масса испытуемого как функция времени? Найдите массу испытуемого после 15 дней голодания.

6. Найдите решения, удовлетворяющие нулевому начальному условию, для следующих уравнений первого порядка:

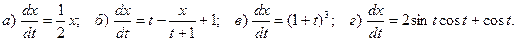
7. Найдите решения для следующих уравнений первого порядка:

а)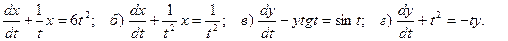

8. Допустим, что уравнение первого порядка 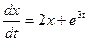отражает скорость роста популяции 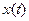в момент времени t. Дайте биологическую интерпретацию каждому члену уравнения. Найдите размеры популяции в моменты t=0,1; t=0,2; t=0,5, если начальный размер составляет .

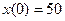9. В популяцию большого размера занесено инфекционное заболевание. Доля людей перенесших заболевание, возрастает со временем, Пусть 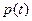обозначает долю людей, переболевших этой болезнью за t лет после ее возникновения в популяции, и пусть 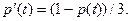Найдите 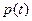для всех моментов t>0, если 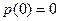. За сколько лет доля переболевших достигнет 90%?

10. Найдите общие решения для следующих уравнений первого порядка:

а)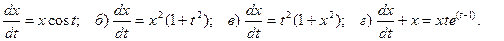

11. Найдите частные, решения удовлетворяющие начальному условию 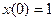для следующих уравнений первого порядка:

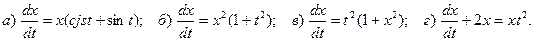
12. Популяция бактерий возрастает от начального размера в 100 ед. до предельного (равновесного) размера в 100000 ед. Пусть в течении первого часа она увеличивается до 120 ед. Считая, что рост популяции подчиняется логистическому уравнению, найдите ее размер как функцию времени.

13. Бактерии, служащие пищей для популяции простейших, поступающие в экспериментальную среду с постоянной скоростью 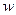. Установлено, что они потребляются со скоростью, пропорциональной квадрату их концентрации. Концентрация 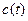бактерий в среде в момент t удовлетворяет, таким образом, уравнению первого порядка 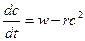, где r – положительная постоянная пропорциональности. а) Выразите концентрацию бактерий 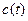через 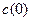. б) Какова равновесная концентрация бактерий, т.е. при каком значении с производная 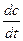обращается в нуль?

14. Найдите общие решения следующих дифференциальных уравнений второго порядка:

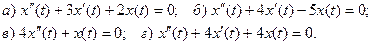
15. Найдите решения, удовлетворяющие начальным условиям 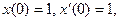для следующих дифференциальных уравнений:

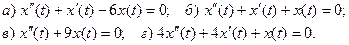
16. Найдите решения, удовлетворяющие начальным условиям 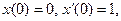для следующих дифференциальных уравнений:

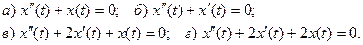
17. Найдите дифференциальное уравнение второго порядка вида 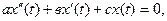имеющие частные решения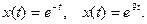

18. Докажите, что все решения уравнения 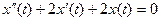приближаются к нулю, когда t стремится к бесконечности.

19. Найдите решения уравнений, удовлетворяющие заданным начальным условиям:

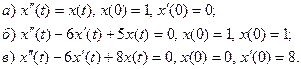
20. Найдите решения уравнений, удовлетворяющие заданным начальным условиям:

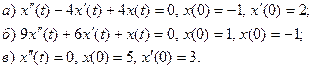
21. Найдите решения уравнений, удовлетворяющие заданным начальным условиям:

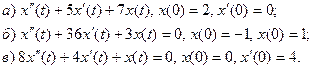
22. В эксперименте с голоданием масса двух испытуемых за 30 дней убывала со 140 и 170 фунтов соответственно до 110 и 125 фунтов. Установлено, что скорость потери массы каждым испытуемым была пропорциональна его массе. Определим 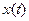как суммарную массу испытуемых после t дней голодания. Найдите дифференциальное уравнение второго порядка, которому удовлетворяет 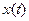. Чему равна суммарная масса после 15 дней голодания?

23. У некоторых птиц общее время, затрачиваемое на питание, колеблется от минимального значения 2 ч. В день (летом) до максимального значения 8 ч. В день (зимой). Считая, что изменения затрат времени на питание описываются уравнением гармонического осциллятора, определите длительность суточных затрат на питание как функцию времени года.

24. В благоприятных условиях выращивают две популяции мух. Для популяции I удельная скорость роста составляет 0,1 (время выражается в днях). Для популяции II аналогичная скорость составляет 0,08. Определим 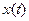как суммарную численность популяций в момент t. Найдите дифференциальное уравнение второго порядка, которому удовлетворяет .

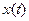25. В условиях задачи 24 найдите общую численность популяции после 10 и после 20 дней роста, если в начальный момент популяции насчитывали по 1000 особей.