Задачи для самостоятельного решения. 2.4.1)Разложите на простейшие дроби:
2.4.1)Разложите на простейшие дроби:
а) 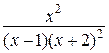 ; б)
; б) 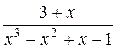 ; в)
; в) 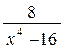 .
.
2.4.2)Представьте дробь 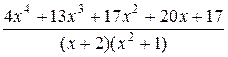 в виде суммы многочлена и простейших рациональных дробей.
в виде суммы многочлена и простейших рациональных дробей.
Тест для самоконтроля
по теме «Рациональные дроби»
1. Дробь 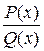 , у которой степень многочлена
, у которой степень многочлена 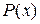 меньше степени многочлена
меньше степени многочлена 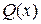 , называется:
, называется:
а) неприводимой; б) неправильной; в) правильной;
г) простейшей; д) целой.
2. Из перечисленных дробей правильными являются:
а) 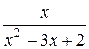 ; б)
; б) 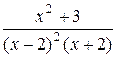 ; в)
; в) 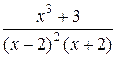 ;
;
г) 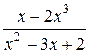 ; д)
; д) 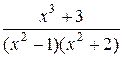 ; е)
; е) 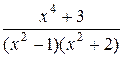 .
.
3. Целая часть неправильной дроби 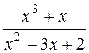 имеет вид:
имеет вид:
а) 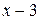 ; б)
; б) 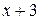 ; в) 1; г)
; в) 1; г) 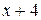 ; д)
; д) 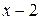 .
.
4. Общий вид разложения 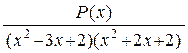 на простейшие состоит из дробей (выбрать нужные):
на простейшие состоит из дробей (выбрать нужные):
а) 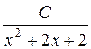 ; б)
; б) 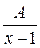 ; в)
; в) 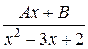 ;
;
г) 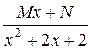 ; д)
; д) 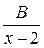 ; е)
; е) 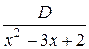 .
.
5. Общий вид разложения дроби 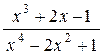 на простейшие имеет вид
на простейшие имеет вид
а) 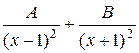 ; б)
; б) 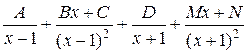 ;
;
в) 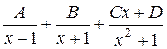 ; г)
; г) 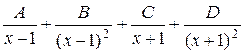 .
.
6. Общий вид разложения дроби 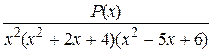 на простейшие имеет вид:
на простейшие имеет вид:
а) 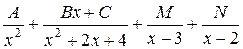 ;
;
б) 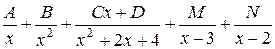 ;
;
в) 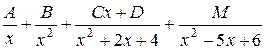 ;
;
г) 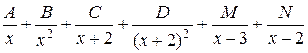 .
.
7. Общий вид разложения 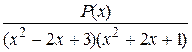 на простейшие имеет вид:
на простейшие имеет вид:
а) 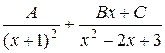 ; б)
; б) 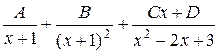 ;
;
в) 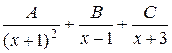 ; г)
; г) 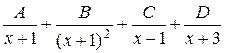 .
.
8. Разложение дроби 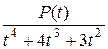 на простейшие состоит из дробей:
на простейшие состоит из дробей:
а) 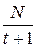 ; б)
; б) 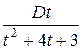 ; в)
; в) 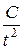 ; г)
; г) 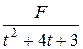 ;
;
д) 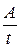 ; е)
; е) 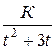 ; ж)
; ж) 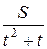 ; з)
; з) 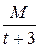 .
.
Образец билета для контроля раздела
«Комплексные числа и многочлены»
Итак, вы изучили темы «Комплексные числа. Многочлены. Рациональные дроби» и выполнили индивидуальное задание №1. Сдайте его на проверку своему преподавателю. Если преподаватель сочтет необходимым, вам нужно будет индивидуальное задание доработать.
Теперь можно готовиться к защите раздела, которая вам предстоит после того, как индивидуальное задание будет зачтено. Ниже мы приводим, в качестве примера, один из билетов для защиты.
Билет состоит из двух частей. Первая часть является обязательной. По результатам ответов на вопросы и решения задач этой части студент может получить оценку «удовлетворительно» или «хорошо». Для получения оценки «отлично» необходимо решить дополнительно хотя бы одну задачу из второй части билета. В эту часть входит несколько задач, и вы можете решить любую из них по своему желанию (или возможностям).
Каждая задача билета оценена в баллах. Оценивается даже частичное (но правильное!) решение задачи. Для получения оценки «удовлетворительно» нужно набрать не менее 56 баллов, оценка «хорошо» ставится, если набрано от 56 до 70 баллов. Оценка «отлично» ставится, если студент набрал 85 баллов и выше.
Для успешной защиты раздела рекомендуем еще раз повторить ответы на вопросы первого и второго уровня (стр. 8, 40 и стр. 42, 58), т.к. эти вопросы могут входить в соответствующие части билетов для защиты.
Билет для контроля раздела
Часть 1.
1) (15б) Опишите с помощью неравенства множество точек полуплоскости, расположенной справа от мнимой оси; ниже действительной оси.
2) (20б) Выполните действия 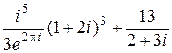 .
.
3) (20б) Пусть 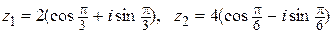 . Какие из следующих равенств верны:
. Какие из следующих равенств верны:
а) 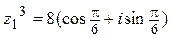 , б)
, б) 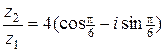
в) 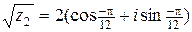 ?
?
4) (15б) Запишите общий вид разложения на простейшие правильной дроби 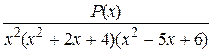 .
.
5) (20б) Остаток от деления некоторого многочлена Р(x) на (x2 – 2x – 8)равен (x +5). Докажите, что остаток от деления этого многочлена на 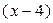 равен 9.
равен 9.
Часть 2.
6) (25б) Сколько корней имеет уравнение z6 +2z3 +1 = 0? Найдите их.
7) (25б) Докажите 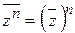 .
.
8) (25б) Дробь 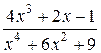 разложите в сумму простейших.
разложите в сумму простейших.
*) Следовательно, задача «найти корни многочлена Р(z)» и задача «решить уравнение Р(z)=0» эквивалентны.
*) При этом так же допишем недостающие члены многочлена с нулевыми коэффициентами. Вообще говоря, так делать не обязательно, но мы сделаем это для наглядности и лучшего понимания процедуры деления.
*) .
**) Значение х= –1 выбрано потому, что при этом значении обращается в ноль второе слагаемое суммы в левой части равенства (**); а значения х=0 и х=1выбраны лишь из соображений простоты вычислений.
