Анықталған интегралдың анықтамасы. функциясы кесіндісінде анықталсын, мұнда . Төменгі амалдарды орындаймыз.

1. 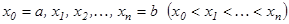нүктелерімен кесіндісін элементар кесінділерге (бөліктерге) бөлеміз: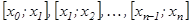

| | • | • | • | • | • | • | • |

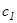
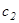
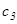
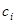
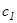
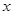
О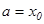

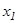
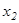
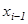
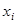
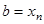
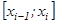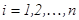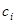
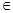
2. Әрбір , элементар кесіндінің ішінде жатқан, кез келген бір 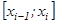нүктесін аламыз және осы нүктедегі функцияның мәнін есептейміз, яғни 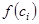шамасын табамыз.

3. Функцияның табылған 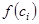мәндерін сәйкес элементар кесінділердің ұзындығына, яғни 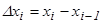көбейтеміз: .

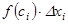4. Барлық осындай көбейтінділердің 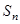қосындысын құрамыз:

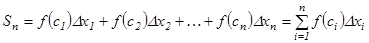
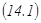
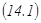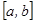қосындысы функциясының кесіндісіндегі интегралдық қосындысы деп аталады. Элементар кесінділердің ең үлкен ұзындығын 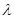деп белгілейміз: .

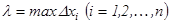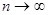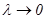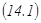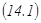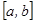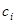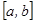5. ұмтылғанда, яғни ұмтылғанда интегралдық қосындысының шегін табамыз. Егер - интегралдық қосындысы үшін ақырлы шек бар болып, ол кесіндісін дербес бөліктерге бөлу жолына және нүктелерін таңдап алу тәсіліне тәуелсіз болса, онда ол шекті функциясының кесіндісіндегі анықталған интегралы деп атайды және оны 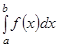символымен белгілейді. Сонымен,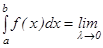

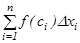
Мұндағы 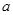санын интегралдың төменгі шегі, ал 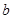санын — жоғары шегі дейді. — интеграл астындағы функция, 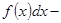интеграл астындағы өрнек деп аталады.

Егер 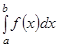саны бар болса, онда функциясы 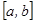кесіндісінде интегралданатын функция деп аталады. Енді анықталған интегралдың бар болуы туралы теореманы келтірейік.

Теорема (Коши). Егер функциясы 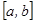кесіндісінде үзіліссіз болса, онда оның осы аралықта анықталған интегралы 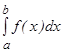бар. Егер функциясының 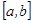аралығында санаулы бірінші текті үзіліс нүктелері болса, онда бұл функция 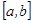аралығында интегралданады.

Анықталған интегралдың анықтамасынан шығатын оның кейбір қасиеттері:

1. Анықталған интеграл өзінің интегралдау айнымаласына тәуелді емес, ол тек интегралдың шектері мен функциясынан тәуелді, яғни ,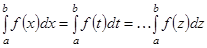

2. Егер 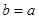болса, онда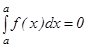

3. Кез келген нақты 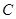саны үшін: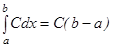

Анықталған интегралдың қасиеттері.Бұл бөлімде интегралданатын функцияларды қарастырамыз.

1. 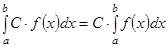, мұнда 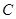- нақты сан.

2. .

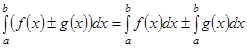3.

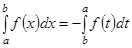
4. Егер 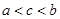теңсіздігі орындалса, онда .

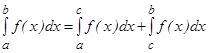5. Егер 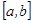кесіндісінде 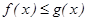болса, онда .

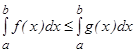6. Орта мән туралы теорема. Егер функциясы 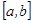кесіндісінде үзіліссіз болса, онда 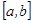кесіндісінен 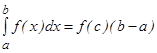теңдігі орындалатындай 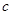саны табылады.

Ньютон – Лейбниц формуласы.Егер функциясы 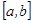кесіндісінде интегралданатын болса, онда ол осы кесіндінің ішінде жатқан кез келген 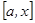кесіндісінде де интегралданады. 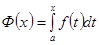, мұнда 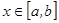функциясын қарастыралық.

Теорема. Егер 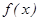функциясы 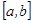кесіндісінде үзіліссіз болса, онда 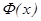функциясы да 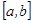кесіндісінде үзіліссіз болады.

Теорема. 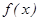функциясы 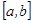кесіндісінде үзіліссіз болсын. Онда

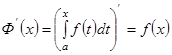
Салдар. 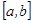кесіндісінде үзіліссіз болған кез келген 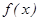функциясының осы кесіндіде алғашқы функциясы бар, ол 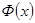функциясына тең. Енді интегралды есептеудің негізгі формуласы Ньютон – Лейбниц формуласына көшелік.

Негізгі теорема. функциясы 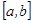кесіндісінде үзіліссіз және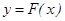

оның осы кесіндідегі алғашқы функциясы болсын. Онда

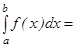
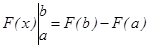
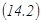
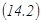формуласы Ньютон- Лейбниц формуласы деп аталады. Ньютон-Лейбниц формуласы анықталған интегралды есептеу үшін өте қолайлы құрал. Оны қолдану үшін интеграл астындағы жатқан функцияның бір алғашқы функциясын білу жеткілікті.

1-мысал. 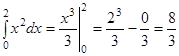.