Уравнение кривой и поверхности

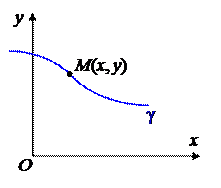Определение. Пусть g – некоторая кривая на плоскости, а j(x, y) – функция двух переменных. Говорим, что уравнение

j(x, y) = 0 (1)

есть уравнение кривой g в неявном виде, если координаты любой точки MÎ g удовлетворяют (1), и обратно, каждая

пара (x, y) чисел, удовлетворяющих (1), задает точку M(x, y) на кривой.

Подчеркнем, что при составлении уравнений следствие обязательно надо проверять в обе стороны.

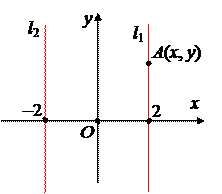Пример 1. Уравнение

x²– 4 = 0 (*)

задает на плоскости пару прямых (см.чертеж). Координаты любой точки A(x, y)Î l₁ удовлетворяют (*), но нельзя

сказать, что (*) есть уравнение l₁ , поскольку есть еще точки, координаты которых удовлетворяют (*), но на l₁ эти точки не лежат.

С другой стороны, каждая точка, координаты которой удовлетворяют уравнению

x – 2 = 0, (**)

лежит на фигуре l₁U l₂ , но нельзя сказать что (**) задает эту фигуру, поскольку есть еще точки на l₁U l₂, координаты которых (**) не удовлетворяют.

Пример 2. Составим уравнение окружности g радиуса R с центром в точке O¢(a, b). Пусть M(x, y) – произвольная точка окружности g . Тогда

R =½O¢M½= Û

Û (x – a)² + (y – b)² = R ². (2)

Обратно, если координаты точки M(x, y) удовлетворяют (2), то ½O¢M½= R, а значит, MÎg. Таким образом (2) и есть уравнение нашей окружности.

Если из уравнения (1) удается выразить одну координату через другую, то получим уравнение в явном виде:

y = f (x), (3)

Не всегда удается привести неявное уравнение кривой к явному виду. В каком случае это возможно гласит теорема о неявной функции, изучаемая в курсе математического анализа. Например, с уравнением окружности это сделать нельзя.

Предположим, что точка движется по кривой. Тогда ее координаты изменяются со временем:

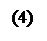
x = j( t ),

y = y( t ).

При этом параметр t изменяется в определенных пределах: tÎI, где I – интервал числовой прямой. Говорим, что (4) есть параметрические уравнения кривой g, если точка M(x, y) лежит на кривой g тогда и только тогда, когда найдется такое tÎI, что будут выполнены оба равенства (4) одновременно. При этом, обязательно к системе (4) надо добавлять интервал изменения параметра. Физический смысл параметра в (4) не всегда время.

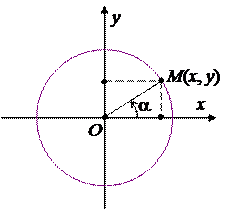Пример 2. Параметрические уравнения окружности радиуса R с центром в начале координат имеют вид:

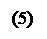
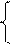x = R·cos a ,

y = R·cos a , aÎR .

Не важно, что для одной и той же точки

может найтись несколько (или даже

бесконечно много) соответствующих ей

значений параметра. Это не запрещается.

Пример 3.Уравнения

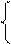x = t² ,

y = t³ , tÎR .

задают полукубическую параболу. Уравнения

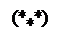
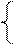x = e^{2 t},

y = e^{3 t}, tÎR .

тоже задают полукубическую параболу, но не всю, а только ее верхнюю половину. Для точки M, лежащей ниже оси, Ox не найдется такого t, для которого выполнено (***).

Определение. Пусть F – некоторая поверхность в пространстве, а F(x, y, z) – функция от трех переменных. Говорим, что

F(x, y, z) = 0 (6)

есть уравнение поверхности F в неявном виде, если координаты любой точки MÎF удовлетворяют (6), и обратно, каждая пара (x, y) чисел, удовлетворяющих (6), задает точку M(x, y, z) на поверхности.

Так же, как и для кривой, при составлении уравнения поверхности, необходимо проверять следствие в обе стороны.

Упражнение. Самостоятельно докажите, что сфера радиуса R с центром в точке O¢(a, b, с) задается уравнением

(x – a)² + (y – b)² + (z – c)² = R ². (7)

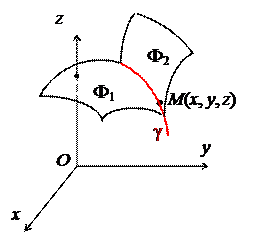Если из уравнения (6) удается выразить одну переменную через две другие, то получим уравнение поверхности в явном виде: z = f (x, y). Вопрос, когда это возможно сделать, изучается в курсе математического анализа. Уравнение сферы невозможно переписать в явном виде.

Кривая в пространстве одним уравнением, как правило, не задается. Бывают исключительные случаи, типа уравнения x² + y² = 0, которое задает прямую – ось Oz. Кривая в пространстве обычно задается системой из двух уравнений

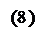
F₁(x, y, z) = 0,

F₂(x, y, z) = 0.

Каждое из уравнений в отдельности задает поверхность. Если координаты

точки удовлетворяют системе, то она лежит на двух поверхностях одновременно, т.е. MÎF₁IF₂. Таким образом, система (8) задает линию пересечения двух поверхностей (хотя заметим, что не всегда это пересечение будет кривой). Аналогично, если мы хотим найти точки пересечения любых двух множеств, заданных своими уравнениями, мы должны объединить данные уравнения в одну систему.

Пример 4. Система уравнений

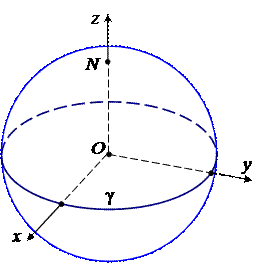
x² + y² + z² = R ².

z = 0.

задает окружность в плоскости Oxy. Первое уравнение системы задает сферу с центром в начале координат, а второе – плоскость Oxy. Их пересечение есть окружность g. Если подставить z = 0 в первое уравнение, то получим

x² + y² = R ². (**** )

Казалось бы, можно сказать, что это и есть уравнение окружности g. Но это не так. Уравнение (****)

задает цилиндрическую поверхность (см. параграф «цилиндрические и конические поверхности»). Подставляя z = 0 в первое уравнение системы, нельзя отбрасывать при этом само уравнение z = 0.

Также кривая в пространстве может быть задана параметрическими уравнениями вида

x = j( t ),

y = y( t ),

z = s( t ), t ÎI ,

где I – интервал числовой прямой. С параметрическими уравнениями поверхности мы встретимся в разделе «Дифференциальная геометрия».

Обозначим – радиус-вектор произвольной точки M(x, y, z) на кривой, т.е. вектор с координатами, составленными из неизвестных (x, y, z), а – вектор с координатами (j( t ), y( t ), s( t )). Тогда параметрические уравнения кривой можно переписать в виде одного векторного уравнения

= , t ÎI.