Дослідження нерозгалуженого кола синусоїдального струму
Мета роботи – дослідним шляхом визначити параметри різних за характером опорів споживачів у колі змінного струму та засвоїти основні закони синусоїдального струму для нерозгалуженого кола.
Теоретичні відомості
В електротехніці найбільш поширеним змінним струмом є струм, що змінюється у часі за синусоїдальним законом. Математично змінний синусоїдальний струм можна записати в такому вигляді:

де і – миттєве значення змінного струму;  – амплітудне значення
– амплітудне значення
струму; 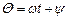 – фаза коливання (рад),
– фаза коливання (рад),  – початкова фаза, тобто значення
– початкова фаза, тобто значення  при
при  ;
; 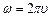 – кутова частота (рад/с);
– кутова частота (рад/с);
 – частота (Гц).
– частота (Гц).
Електричні кола змінного струму характеризуються чотирма основними параметрами: активним опором  , індуктивністю
, індуктивністю  , взаємоіндуктивністю М і ємністю С.
, взаємоіндуктивністю М і ємністю С.
Опір – ідеалізований пасивний елемент, в якому електроенергія незворотно перетворюється в інший вид енергії (теплову, механічну, світлову) і реалізується реальним елементом електричного кола – резистором.
Напруга на опорі за законом Ома дорівнює:

Індуктивність – ідеалізований пасивний елемент, який має властивість накопичувати енергію у магнітному полі. Реалізується реальним елементом електричного кола – котушкою індуктивності. Напруга на індуктивності за законом електромагнітної індукції:

Звідси
 ,
,
де  – струм в індуктивності в момент часу
– струм в індуктивності в момент часу  .
.
Взаємною індуктивністю володіють електромагнітні пристрої, у яких обмотки мають магнітні зв’язки, тобто магнітний потік, який створюється однією котушкою, пронизує другу обмотку. Тоді такий пристрій, окрім індуктивності  і
і  , має також взаємну індуктивність М, причому еквівалентна індуктивність при узгодженій взаємодії
, має також взаємну індуктивність М, причому еквівалентна індуктивність при узгодженій взаємодії  (коли магнітні потоки, створювані обома котушками, співпадають) більша, а при неузгодженій взаємодії
(коли магнітні потоки, створювані обома котушками, співпадають) більша, а при неузгодженій взаємодії  (коли магнітні потоки обох котушок направлені протилежно) – менша за сумарну індуктивність двох котушок.
(коли магнітні потоки обох котушок направлені протилежно) – менша за сумарну індуктивність двох котушок.
 ,
,
тоді
 .
.
Ємність – ідеалізований пасивний елемент, який має властивість накопичувати енергію в електричному колі. Реалізується реальним елементом електричного кола – конденсатором.
Струм в ємності

Звідси
 ,
,
де  – напруга на ємності в момент часу
– напруга на ємності в момент часу  .
.
Векторні діаграми дозволяють наочно показати кількісні та фазові відповідності в колах синусоїдального струму і широко застосовується при пояснюванні фізичних процесів, і висновків основних відповідностей.
Напруги та струми, які синусоїдально змінюються у часі, зображаються на комплексній площині обертовими векторами амплітудних (рис. 3.1, а) або діючих значень (рис. 3.1, б). За позитивний напрямок обертання векторів з кутовою швидкістю  прийнято напрямок обертання проти руху годинникової стрілки. Фазовий кут
прийнято напрямок обертання проти руху годинникової стрілки. Фазовий кут  при такому обертанні відлічують у позитивному напрямку від дійсної осі (рис. 3.1).
при такому обертанні відлічують у позитивному напрямку від дійсної осі (рис. 3.1).

а б
Рис. 3.1. Зображення синусоїдального струму обертовими векторами
з амплітудним (а) та діючим (б) значеннями
Оскільки розрахунки кіл змінного струму виконуються з використанням діючих значень синусоїдальних величин, то ці величини доцільніше зображати векторами діючих значень (рис. 3.1, б).
При розрахунку кіл гармонічного струму необхідно розв’язувати інтегрально-диференціальні рівняння кіл, що в ряді випадків виявляються трудомісткими навіть для простих кіл. Тому для розрахунку кіл гармонічного струму використовується метод комплексних амплітуд, суть якого полягає в тому, що діючі в колі струми і напруги заміняються комплексними величинами. В результаті операції диференціювання і інтегрування замінюються на операції множення і ділення на уявну частоту  , завдяки чому здійснюється перехід від інтегрально-диференціальних рівнянь до алгебраїчних.
, завдяки чому здійснюється перехід від інтегрально-диференціальних рівнянь до алгебраїчних.
Нехай при послідовному з’єднанні споживачів із різним характером опорів (активним, індуктивним і ємнісним (рис. 3.2)), в колі протікає синусоїдальний струм

Згідно з другим законом Кірхгофа можна записати рівняння електричної рівноваги для миттєвих значень напруг:

або


Рис. 3.2. Послідовне з’єднання споживачів у колі змінного струму
Інтегрально-диференціальне рівняння електричної рівноваги можна записати:

де  – комплексний опір кола;
– комплексний опір кола;  – повний опір кола.
– повний опір кола.
Напруга на активному опорі

Напруга на індуктивності

Напруга на ємності

 Отже, як це видно із останніх співвідношень, напруга на активному опорі співпадає за фазою зі струмом, напруга на реактивному індуктивному опорі випереджає, а напруга на реактивному ємнісному опорі відстає за фазою від струму на кут
Отже, як це видно із останніх співвідношень, напруга на активному опорі співпадає за фазою зі струмом, напруга на реактивному індуктивному опорі випереджає, а напруга на реактивному ємнісному опорі відстає за фазою від струму на кут  . Тоді векторні діаграми для нерозгалуженого кола (рис. 3.2) будуть такими, які показані на рис. 3.3.
. Тоді векторні діаграми для нерозгалуженого кола (рис. 3.2) будуть такими, які показані на рис. 3.3.
а б
Рис. 3.3. Векторні діаграми напруг і струму для послідовного кола
Знак зсуву фаз визначається знаком еквівалентного реактивного опору  , Коли
, Коли  , то коло має активно-індуктивний характер, тобто струм по фазі відстає від напруги на кут
, то коло має активно-індуктивний характер, тобто струм по фазі відстає від напруги на кут  (рис. 3.3, а). Коли
(рис. 3.3, а). Коли  , то коло має активно-ємнісний характер, тобто струм випереджає напругу на кут 0
, то коло має активно-ємнісний характер, тобто струм випереджає напругу на кут 0  (рис. 3.3, б). Коли
(рис. 3.3, б). Коли  і
і  має місце режим резонансу, при якому опір кола чисто активний. Режим резонансу буде розглядатися далі.
має місце режим резонансу, при якому опір кола чисто активний. Режим резонансу буде розглядатися далі.
Розділивши величини, які відображають сторони трикутника ОАВ, на комплекс дійового значення струму, що протікає в колі, отримаємо трикутники струмів.
На рис. 3.4 побудовані трикутники опорів при індуктивному і ємнісному характері комплексного опору.

а б
Рис. 3.4. Трикутники опорів: при індуктивному (а)
та ємнісному (б) характері комплексного опору
Із трикутників опору слідує, що
 – модуль комплексного опору чи повний опір,
– модуль комплексного опору чи повний опір,
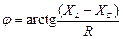 – аргумент комплексного опору.
– аргумент комплексного опору.
Порядок виконання роботи
1. Накреслити схему електричного кола (рис. 3.5) з параметрами згідно з варіантом (табл. 3.1).

Рис. 3.5. Схема електричного кола
Таблиця 3.1
| Номер варіанта | Ампліту-да ЕРС  , В , В | Частота  , Гц , Гц | Опір  , Ом , Ом | Індуктив-ність 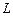 , мГн , мГн | Ємність 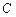 , мкФ , мкФ |
2. Розрахувати діючі значення струму  , ЕРС
, ЕРС  та напруг
та напруг  за допомогою закону Ома. А також кут зсуву фаз між струмом та ЕРС. Результати розрахунку занести в табл. 3.2.
за допомогою закону Ома. А також кут зсуву фаз між струмом та ЕРС. Результати розрахунку занести в табл. 3.2.
Здійснити математичне моделювання послідовного електричного кола (рис. 3.6). Виміряти значення струму в колі та напруг на електричних колах та їх комбінаціях. Результати вимірювань занести в табл. 3.2 та порівняти з результатами розрахунків.

Рис. 3.6. Математичне моделювання послідовного електричного кола
Таблиця 3.2
 А А |  В В |  В В |  В В |  В В |  В В |  В В |  В В |  , град , град | |
| Результати розрахунків | |||||||||
| Марема-тичне моделю-вання | |||||||||
| Похибка |
3. Побудувати графіки миттєвих значень синусоїдального струму  , синусоїдальної ЕРС
, синусоїдальної ЕРС  та напруг на резисторі
та напруг на резисторі  , індуктивності
, індуктивності  і ємності
і ємності  (рис. 3.7).
(рис. 3.7).

Рис. 3.7. Миттєві значення синусоїдального струму i(t),
синусоїдальної ЕРС е(t) та напруг 
4. Визначити фазові співвідношення між струмом  та напругами
та напругами  ,
,  ,
,  та
та  графічним методом
графічним методом
(рис. 3.8):
1) між  та
та  :
:
 ; фази
; фази  та
та  співпадають;
співпадають;
2) між  та
та  :
:
 ;
;  випереджає
випереджає  по фазі на
по фазі на  ;
;
3) між  та
та  :
:
 ;
;  відстає від
відстає від  по фазі на
по фазі на  ;
;
4) між  та
та  :
:
 ;
;  випереджає
випереджає  по фазі на
по фазі на  .
.

Рис. 3.8. Осцилограми результатів математичного моделювання
5. Побудувати векторні діаграми напруги і струму для кожного споживача  та для нерозгалуженого кола в цілому.
та для нерозгалуженого кола в цілому.
Зміст звіту
Звіт повинен містити:
1. Мету і порядок виконання роботи;
2. Результати розрахунку діючих значень напруг на елементах  та їх комбінаціях;
та їх комбінаціях;
3. Результати математичного моделювання нерозгалуженого електричного кола;
4. Графіки миттєвих значень струму, ЕРС та напруг на елементах  послідовного кола;
послідовного кола;
5. Осцилограми результатів математичного моделювання;
6. Векторні діаграми напруги і струму для кожного елемента кола  і для кола в цілому;
і для кола в цілому;
7. Короткі висновки за результатами роботи.
Контрольні питання
1. Якими параметрами характеризуються електричні кола змінного струму?
2. У чому полягає суть методу комплексних амплітуд?
3. Як визначається повний опір нерозгалуженого кола?
4. Поясніть, що таке коефіцієнт потужності.
5. Запишіть закон Ома в комплексній формі для кола з послідовним з’єднанням елементів  і
і  .
.
6. Поясніть порядок побудови векторної діаграми при послідовному з’єднанні елементів  і
і  .
.
Лабораторна робота 4
