Определение скорости при естественном способе задания движения точки

При естественном способе известны траектория и закон движения точки S=f(t).

В выражении (8), где радиус-вектор 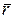однозначно определяет положение движущейся точки М в векторной форме в декартовой системе координат; положение же точки при естественном способе задается законом S=f(t), тогда справедливо равенство

. (14)

Вектор скорости в данный момент времени есть первая производная по времени от закона движущейся точки.

В случае если при нахождении скорости в заданный момент времени, численное значение окажется больше нуля (V> 0), то скорость направлена по касательной к траектории в сторону положительного отсчета расстояния S. При V< 0 – скорость направлена по касательной к траектории в сторону отрицательного отсчета расстояния S.

Ускорение точки

Ускорение точки – векторная величина, характеризующая изменение ее скорости с течением времени.

Рис.5.

Пусть в некоторый момент времени t движущаяся точка находится в положении М и обладает скоростью 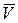, а в момент t₁ приходит в положение М₁, со скоростью (рис.5).

Вектором среднего ускорения точки за промежуток времени 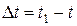называется отношение векторного приращения скорости к промежутку времени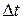

. (15)

Направление вектора среднего ускорения совпадает с направлением вектора приращения скорости .

Ускорение точки в данный момент времени представляет собой вектор численно равный отношению вектора приращения скорости к промежутку времени 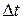, при

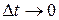
. (16)

С учетом уравнения (8)

. (17)

Вектор ускорения точки в данный момент времени 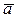лежит в плоскости, по которой происходит бесконечно малое перемещение движущейся точки, направленный в сторону вогнутости кривой.

Ускорение точки в данный момент времени – вектор равный первой производной от вектора скорости по времени или второй производной от радиус-вектора движущейся точки по времени.

Определение ускорения точки при координатном способе задания движения точки

На основании выражений (17) и (2)

. (18)

В свою очередь, вектор ускорения в заданный момент времени также можно представить через проекции ускорений на единичные вектора координатных осей,

. (19)

Сравнивая уравнения (18) и (19), с учетом (11) получаем

, , . (20)

Таким образом, проекции ускорения точки на координатные оси представляют собой первые производные от проекций скорости или вторые производные от соответствующих координат движущейся точки по времени.

Рис.6.

Зная проекции вектора ускорения на оси координат, определим модуль ускорения в заданный момент времени и косинусы углов с осями координат (рис.6)

, (21)

. (22)