Практический пример. Задача изменения температуры тела в зависимости от температуры воздуха

Согласно закону излучения тепла, скорость изменения температуры тела в воздухе пропорциональна разности между температурой воздуха и тела:

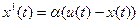(4.5)

где x(t) – температура тела в момент времени t, u(t) – температура воздуха в этот же момент, 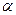- положительный коэффициент, определяемый свойствами тела. Если, например, 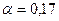и температура воздуха зависит от времени t как 20 – 1/(1+t²), то уравнение запишется в виде

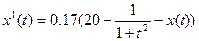(4.6)

Используя вышесказанное, решить следующие задачи.

1. Пусть в момент времени температура воздуха была равна 30⁰, а впоследствии опускалась на 0.01⁰ за каждую секунду, то есть при 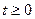выполнено u(t)=30-0.01t. пусть для рассматриваемого тела .

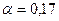Требуется выяснить, сколько потребуется времени для того, чтобы тело, имевшее в момент времени t =0 температуру 100⁰, остыло до температуры 90⁰.

2. Рассматривается уравнение изменения температуры тела. Полагается, что для рассматриваемого тела 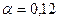. Пусть при 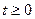выполнено u(t)=30-0.1+5 sin t. Написать вариант программы для решения этой задачи, предприняв некоторые меры по контролю точности. Первоначально вычисления проводить с шагом h=1, затем они повторяются с шагом h=1/2 и так далее до тех пор, пока модуль разности двух последних приближений в точке х(5) не окажется меньшим, чем заданное число eps.

3. Рассматривается дифференциальное уравнение, описывающее вымывание инертного материала из резервуара, который взбалтывается:

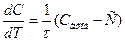(4.7)

где С - концентрация инертного материала (компонента А) в контейнере и вытекающем из этого контейнера потоке (мг/мл);

С_вход – концентрация компонента А во входящем в контейнер потоке (мг/мл);

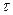- продолжительность обработки сточных вод в системе ( );

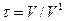V – объем контейнера (константа) (мл);

V¹ – скорость входящего и выходящего потока (мл/с);

Начальная концентрация компонента в резервуаре, а также параметры системы: концентрация компонента А во входном потоке, объем резервуара и скорость потока приведены в таблице 4.1.

Таблица 4.1- Параметры системы

Название параметра	Значение параметра
Первоначальная концентрация компонента А в резервуаре	100 мг/мл
Концентрация компонента А во входном потоке	0 мг/мл
Объем резервуара	10 л
Скорость потока	100 мл/с

Найти концентрацию компонента в каждый момент времени, решая дифференциальное уравнение численным методом. Построить график. Полученные результаты сравнить с аналитическим решением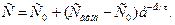

Контрольные вопросы

4.3.1 В каких случаях применяют численные методы решения дифференциального уравнения?

4.3.2 Перечислить наиболее известные методы решения дифференциальных уравнений.

4.3.3 В чем суть метода Эйлера? В чем преимущество этого метода и в чем его недостаток?

4.3.4 В чем суть метода Рунге-Кутта? В чем преимущество этого метода и в чем его недостаток?

4.4.5 Привести пример физического закона, который описывается дифференциальным уравнением.

4.4.6 Сформулировать математически следующее явление: скорость изменения температуры тела в воздухе пропорциональна разности между температурой воздуха и тела.

4.4.7 Сформулировать математически второй закон Ньютона: сила, действующая на тело, равна произведению массы тела на сообщаемое этой силой ускорения, для силы, изменяющейся со временем по известному закону и направленной вдоль фиксированной прямой.

4.4.8 Что понимается по термином «начальное условие»?

Варианты заданий

С помощью пакета MS Excel, а также языка программирования реализовать алгоритмы численного решения дифференциального уравнения и построить графики для приближенного решения по методу Эйлера и Рунге-Кутта, результаты сравнить.

После уравнения в скобках записаны исходные данные для решения: x₀ - начальное значение аргумента, y_{0 –} начальное значение функции от x_0, далее – отрезок, на котором решается уравнение, h – шаг.

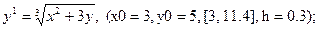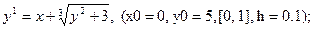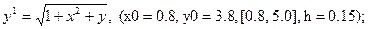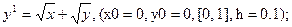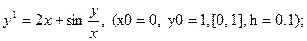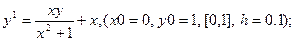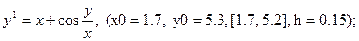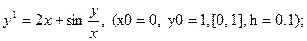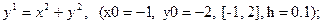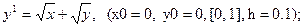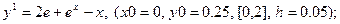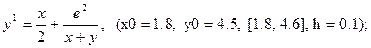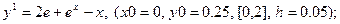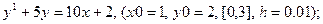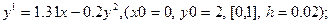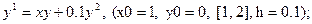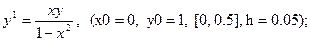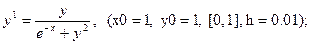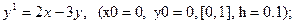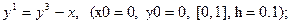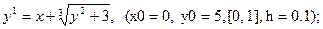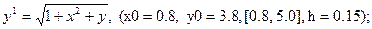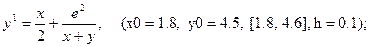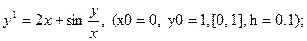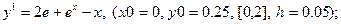Задание 5. Построение поверхности

Цель работы – ознакомиться с методикой построения поверхности в MSExcel и приобрести навыки построения поверхности.

В курсе информатики рассматривалось построение графиков – линий, использование двух координат. Но часто возникает необходимость построения поверхности – использование трех координат.

Построение поверхностей

Построение поверхностей предполагает использование следующей методики:

1. Подготовить диапазон изменения функции по двум координатам, расположив изменения одной координаты вдоль некоторого столбца вниз, а другой – вдоль, прилегающий строки вправо.

2. Ввести на пересечении координат необходимую формулу для построения поверхности и с помощью маркера автозаполнения выполнить ее копирование на всю область построения поверхности.

3. Выделить подготовленные данные и воспользоваться мастером построения диаграмм ( тип диаграммы – Поверхность).

5.2 Задание 1: построить поверхность

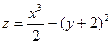(5.1)

Решение:

1. Подготовить диапазон изменения функции: от -1 до 1.

2. Формула для расчета значения z введена в ячейку С3: =($B3^3/2-(C$2+2)^2.

Подготовленный диапазон и построенная поверхность представлены на рисунке 5.1.