Следует провести расчеты, разобранные в примере 2.2, с вашими условиями
Пример 2.2 Заданы квадратная матрица системы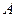 
порядка 
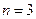с диагональным преобладанием и вектор-столбец свободных членов 
:
.
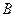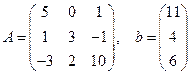Требуется
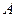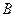- Ввести в компьютер массивы исходных данных и , установить 1 в качестве начала отсчета индексов массивов. Вычислив определитель, проверить невырожденность матрицы .
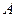- Представить матрицу 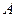в виде суммы матриц: диагональной матрицы
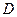и двух строго треугольных с нулевой диагональю 
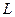и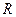 
(левой и правой). Вычислить коэффициенты рекуррентных формул Якоби (2.22) и Зейделя (2.24) по формулам (2.23) и (2.25). - Вычислить
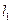- нормы и собственные значения матриц 
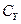и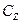 
, используя функци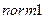и 
и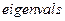 
. Сделать выводы о сходимости процессов итераций по методам Якоби и Зейделя. - Принять
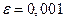за точность решения системы 
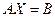по 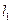- норме и по 
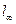- норме. Оценить необходимое количество итераций по формуле (2.13) и рассчитать их, контролируя достигнутую точность по формуле (2.12). - Взять другую систему с матрицей без диагонального преобладания (можно, например, в матрице 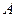уменьшить вдвое или втрое диагональные элементы) и убедиться в возможной расходимости итерационных методов.
- Осуществить симметризацию Гаусса в системе из п.5 и убедиться в сходимости итераций по методу Зейделя.
Решение. Начальные приближения могут быть выбраны произвольно. Для определенности примем за начальные приближения векторы свободных членов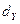 
и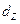 
. Программа решения системы приведена на рис. 2.3 - 2.5.
 |
| Рис. 2.3 |
На рис. 2.3 рассмотрен пример система с диагональным преобладанием. Кроме того нормы матриц 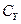и 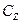, а также собственные значения 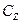по модулю меньше 1. Это говорит в пользу сходимости итераций. Расчет подтверждает наши выводы.
На рис. 2.4 приведен пример системы, для которой итерационные процессы должны расходятся (почему?), и подтверждение сделанного предположения.
 |
| Рис. 2.4 |
И, наконец, на рисунках (2.5)-(2.6) приведены результаты применения упомянутой симметризации Гаусса к системе, которую не удалось решить итерационными методами.
 |
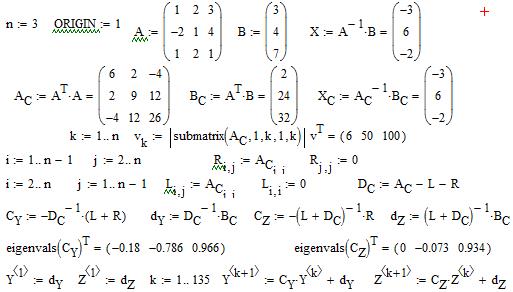| Рис. 2.5 |
 |
| Рис. 2.6 |
Отметим, что после симметризации Гаусса собственные значения матриц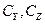 
стали по модулю чуть меньше 1. Это и обеспечивает сходимость, хотя нормы матриц остались больше 1. С последним обстоятельством связана неудача в оценках близости к точному значению корня и требуемого количества итераций (Рис. 2.6).