Рямые методы решения систем алгебраических уравнений.

Выделяют четыре основные задачи линейной алгебры:

– решение системы линейных уравнений (1.20) при m=n, т.е. квадратной порядка n

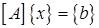(2.1)

– вычисление определителя матрицы

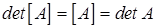
– нахождение обратной матрицы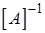

– определение собственных значений и собственных векторов матрицы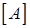

Известно, что если 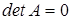, то система линейных уравнений или не имеет решения, или имеет бесчисленное множество решений. Если 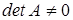, то система имеет решение, причем единственное.

Для системы двух уравнений можно это проиллюстрировать геометрически. Каждому уравнению соответствует прямая в плоскости 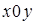, а точка пересечения этих прямых есть решение системы (для системы 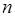уравнений решение есть точка пересечения всех n гиперплоскостей в 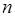-мерном пространстве). Если 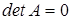, то наклоны прямых равны и они либо параллельны, либо совпадают. В противном случае прямые имеют единственную точку пересечения.

Кроме существования единственности решения важное место занимает еще устойчивость решения относительно погрешностей правой части и элементов матрицы. Перепишем линейную систему в виде

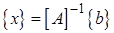(2.1а)

Вариация этого равенства и вариация обратной матрицы дает

,

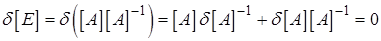откуда получим

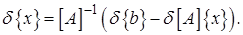(2.2)

Формально устойчивость есть, так как при 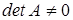обратная матрица существует. Но если матрица 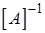имеет большие элементы, то всегда можно указать такие виды погрешностей, которые сильно изменяют решение. В этом случае систему называют плохо обусловленной (м.б., было известно еще Гауссу) (см.Лк 1) /4/. .

Для плохо обусловленных систем 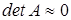, однако признак 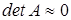является необходимым, но недостаточным.

Плохо обусловленная система геометрически соответствует почти параллельным прямым. При этом небольшое изменение наклона или сдвиг одной прямой сильно меняет положение точки пересечения (см. рис., пунктир):

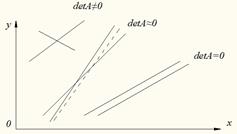
В многомерном случае геометрическая картина может быть более сложной. Так, для трех переменных возможен случай плохой обусловленности, когда соответствующие трем уравнениям плоскости пересекаются под большими углами (то есть далеки от параллельности), но линии их попарного пересечения почти параллельны

.

Методы решения линейных систем делятся на прямые и итерационные.

Прямые методы дают решение за конечное число действий, просты и наиболее универсальны. Для систем небольшого порядка 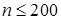применяются практически только прямые методы.

Итерационные методы будут рассмотрены позже; они выгодны для систем специального вида со слабо заполненной матрицей очень большого порядка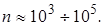

В течение последних десятилетий для решения плохо обусловленных систем стали применять методы регуляризации.

Из школьного курса известно решение системы линейных уравнений по правилу Крамера через отношение определителей. Даже если использовать для вычисления определителей наиболее быстрый метод исключения, то для нахождения всех требуемых по правилу Крамера определителей надо совершить 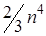действий, тогда как, например, по методу Гаусса, эту систему можно решить примерно за 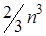арифметических действий, т.е. на порядок ниже. Таким образом, формула Крамера удобна для теоретического исследования свойств решения, но крайне невыгодна для его численного нахождения.

Метод исключения Гаусса. Пусть надо решить систему линейных уравнений (2.1)

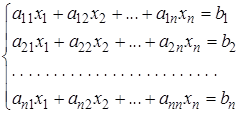(2.3)

или короче

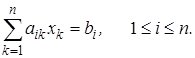(2.3а)

Начнем исследование этой системы с частного случая, когда численное решение находится особенно просто. Пусть матрица 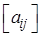верхняя треугольная, то есть все ее элементы ниже главной диагонали равны нулю. Тогда из последнего уравнения сразу находим 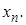Подставив его в предпоследнее уравнение, находим 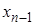и так далее. Общая формула имеет вид

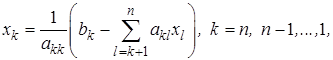(2.4)

есл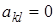и при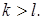

Метод Гаусса в общем виде основан на приведении матрицы системы к треугольной. Вычтем из второго уравнения исходной системы (2.3) первое, умноженное на такое число, чтобы уничтожился коэффициент при 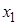, затем таким же образом вычтем первое уравнение из третьего, четвертого и так далее. Таким образом исключены все коэффициенты первого столбца ниже главной диагонали.

Затем при помощи второго уравнения исключим из третьего, четвертого и так далее уравнений коэффициенты второго столбца. Продолжая последовательно этот процесс, исключим из матрицы все коэффициенты, лежащие ниже главной диагонали.

Общие формулы процесса после исключения коэффициентов из 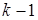столбца:

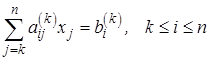(2.5)

Умножим 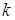-ю строку на число

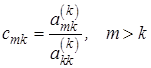(2.6)

и вычтем из 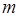-й строки. Первый ненулевой элемент этой строки обратится в нуль, а остальные изменятся по формулам

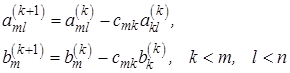(2.7)

Исключение из 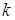-го столбца по формулам (2.7) называется циклом процесса, а выполнение всех циклов прямым ходом исключения.

При приведении системы к верхнему треугольному виду освободятся клетки в нижней левой половине матрицы системы (2.3), на освободившиеся места матрицы поставим множители 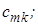их следует запоминать, ибо они потребуются при обращении матрицы или уточнении решения. Получим

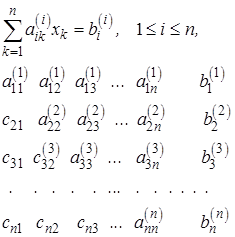(2.8)

Треугольная система (2.8) легко решается обратным ходом по формулам (2.4), в которых всем коэффициентам надо приписать вверху в скобках индексы строки.

Примечания:

1. Исключение по формулам (2.6) и (2.7) нельзя проводить, если в ходе

расчета на главной диагонали оказался нулевой элемент 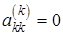. Но так как в первом столбце промежуточной системы (2.5) все элементы не могут быть нулями (это означало бы 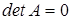), то перестановкой строк можно переместить ненулевой элемент на главную диагональ и продолжить расчет.

2. Если элемент на главной диагонали 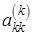мал, то эта строка умножается

на большие числа 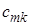, что приводит к значительным ошибкам округления при вычитаниях. Чтобы избежать этого, каждый цикл всегда начинают с перестановки строк. Среди элементов столбца 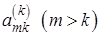находят главный, то есть наибольший по модулю в 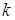-м столбце, и перестановкой строк переводят его на главную диагональ, после чего делают исключения. В методе Гаусса с выбором главного элемента погрешности округления обычно невелики, но для плохо обусловленных систем устойчивость решения недостаточна.

3. Погрешность округления можно еще уменьшить, если выбирать в

каждом цикле элемент 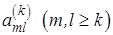, максимальный по модулю. Однако точность при этом возрастает не так значительно, как при выборе главного элемента (прим. 2), а расчет заметно усложняется, ибо требуется перестановка не только строк, но и столбцов. Эта модификация метода Гаусса невыгодна при компьютерных расчетах.

4. Для контроля расчета полезно найти невязки решения

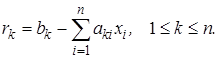(2.9)

Если они велики, то это означает грубую ошибку в расчете (ошибка в программе, компьютерный сбой). Если невязки малы, а система хорошо обусловлена, то решение надежно. Но для плохо обусловленных систем малость невязок еще не гарантирует хорошей точности.

5. Метод Гаусса с выбором главного элемента надежен, прост и наиболее

выгоден для нелинейных систем общего вида с плотно заполненной матрицей. Он требует примерно 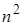ячеек оперативной памяти ПК, при вычислениях производится 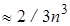арифметических действий; из них половина сложений, половина умножений, и 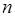делений.

6. Определитель матрицы 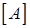легко вычисляется методом исключения

Гаусса:

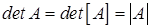
Так как вычитание строки из строки не меняет значения определителя, то в процессе исключения (2.6) и (2.7) абсолютная величина определителя также не меняется, а знак может изменится благодаря перестановке строк. Определитель треугольной матрицы равен произведению диагональных элементов:

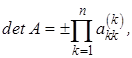(2.10)

где знак зависит от того, четной или нечетной была суммарная перестановка строк. Требуется 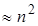ячеек памяти и 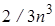арифметических действий. Вычисление же определителя формально, как суммы всевозможных произведений элементов, взятых из разных строк и столбцов, уже при небольших 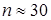требует колоссального числа действий – более 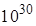, что не под силу даже самым мощным компьютерам. Метод же исключений Гаусса позволяет довольно легко вычислять определители матриц сотен и тысяч порядков /3/.

7. Вычисление обратной матрицы. Обозначим ее элементы 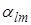. Тогда

соотношение 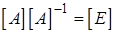можно записать так /3/:

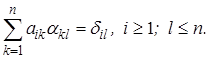(2.11)

Очевидно, если рассматривать 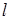-й столбец обратной матрицы 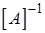как вектор, то он является решением линейной системы (2.11) с матрицей 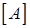и специальной правой частью 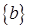(в которой на 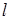-м месте стоит единица, а на остальных - нули).

Таким образом, для обращения матрицы надо решить 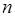систем линейных

уравнений с одинаковой матрицей 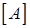и разными правыми частями. Приведение матрицы 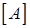к треугольному виду по (2.6) и (2.7) сделано при этом один раз, и больше не повторяется. В дальнейшем при помощи чисел 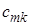по (2.6) преобразуются все правые части, и для каждой правой части делается обратный ход. Для обращения матрицы этим методом требуется 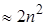ячеек памяти и 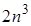арифметических действий, причем контролировать невязки невыгодно: перемножение матриц 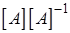требует столько же действий, как и обращение матрицы.

Заметим, что обращение матрицы методом исключения сводится к решению 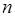систем линейных уравнений, но требует лишь втрое больше действий, чем решение одной системы уравнений, потому что в последнем случае большая часть вычислений связана с приведением матрицы к треугольной, а при обращении матрицы это делается только один раз. Поэтому, если требуется решить систему с одной и той же матрицей несколько раз, то выгодно привести ее к треугольной форме (2.8) только однажды, используя числа 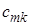во всех последующих вычислениях.

8. Правило Крамера /1, 2, 7/. Система линейных неоднородных уравнений

порядка 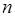в виде матричного равенства

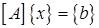(2.12)

с неособенной матрицей 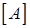решается умножением (2.12,) на 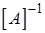слева:

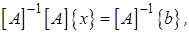
и так как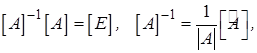

причем 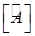- матрица, союзная с 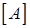, получим

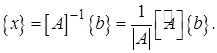(2.13)

Покажем, что последняя формула есть матричная форма известного правила

Крамера через отношение определителей:

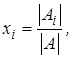(2.14)

где 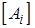- матрица, полученная из 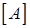заменой элементов 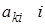-го столбца свободными членами, 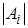- ее определитель.

Действительно, матричное равенство (2.13) равносильно 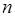равенствам

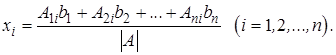
Так как 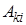суть алгебраические дополнения элемента 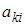в определителе

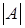, мы получаем

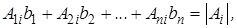
что и требовалось доказать. Таким образом, в правиле Крамера приходится вычислять 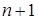определитель 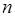-го порядка, тогда как в методе Гаусса объем вычислений лишь немногим превышает вычисление одного определителя. По сути дела, в процессе Гаусса производится вычисление всех определителе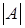й и 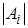одновременно, причем деление на 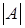производится постепенно, по одному множителю на каждом шаге, то есть для численного решения систем применение правила Крамера нецелесообразно /1/, однако оно удобно для теоретического исследования свойств решения /2/.

2.2. Модификации метода Гаусса. Сравнение прямых методов.

Метод оптимального исключения имеет ту же скорость, что и метод Гаусса,

но матрица вводится в компьютер не вся, а построчно, что требует вдвое меньше оперативной памяти. Практическая ценность этого преимущества весьма невелика из-за обращений к внешней памяти и невозможности выбора главного элемента.

Метод окаймления построен на последовательном рассмотрении матриц

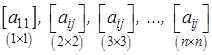
из которых каждая следующая получается из предыдущей путем окаймления. Путем накопления решений усеченных систем может быть получена как обратная матрица 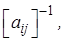так и решена система уравнений 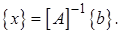Этот метод целесообразно использовать в случае, когда надо решать систему, для которой уже ранее решена усеченная система, получающаяся из заданной путем вычеркивания одного уравнения и одного неизвестного. Например, если в методе Галеркина или Ритца оказалось, что решение в результате использования 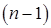-й координатной функции недостаточно точно, и для уточнения достаточно добавления еще одной координатной функции, то новая система получается из предшествующей системы окаймлением. Принципиально методы оптимального исключения и окаймления различаются мало и имеют одинаковые характеристики /3/.

Эскалаторный метод тесно связан с методом окаймления и был предложен

Дж. Морисом в 1947г. Существенным достоинством метода автор считает наличие надежного контроля, при помощи которого можно регулировать точность вычислений; в частности, метод дает довольно надежный результат, даже если определитель матрицы системы уравнений относительно мал /1/.

Хотя метод, по-видимому, применим для систем общего вида, в /1/ он

изложен для систем уравнений с симметричной матрицей коэффициентов при неизвестных в виде

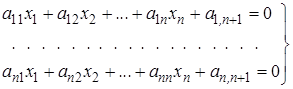(2.15)

или в матричном виде

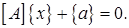
Путем введения вспомогательной матрицы 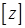и замены неизвестных

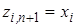и соответствующих преобразований устанавливается связь эскалаторного метода с методом Гаусса в свете разложения матрицы на множители по схеме единственного деления. Рекуррентные формулы этого разложения для последовательного определения чисел 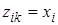после вычисления 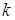столбцов вспомогательной матрицы, то есть 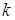строк ее транспонированной матрицы, позволяют перейти к вычислению элементов 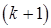-го столбца матрицы 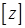(явная связь с методом окаймления) /1/.

Метод ортогонализации /3/ поначалу привлек внимание в надежде на то,

что позволит решать плохо обусловленные системы, но вскоре выяснилось, что, кроме того, что он втрое медленнее метода Гаусса, при больших 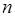сам процесс ортогонализации приводит к потере точности, и лучше использовать методы регуляризации (см. ниже Плохо обусловленные системы).

Метод Гаусса-Жордана /3, 4/ основан на преобразовании матрицы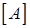

путем исключения так, что 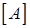преобразуется в единичную, а 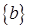в столбец, элементы которого равны значениям искомого вектора 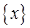, то есть 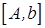преобразуется в 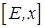. Модификация Жордана имеет ту же скорость, что исключение Гаусса: при решении линейных систем он не дает никаких преимуществ, но при обращении матриц требует вдвое меньше памяти.

Метод прогонки. Для решения хорошо обусловленных линейных

неоднородных систем общего вида метод исключения Гаусса является одним из лучших. Но для систем специального вида существуют более быстрые методы. Если матрица 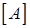содержит много нулевых элементов, расположенных плотными массивами на заранее известных местах, метод Гаусса можно организовать так, чтобы не включать эти элементы в расчет: объем вычислений и требуемая память уменьшаются, зачастую очень значительно /3/.

В дополнение к классификации п.1.1, в задачах механики часто встречаются

матрицы:

а) ленточные (ширина ленты 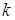элементов);

б) почти треугольные (ненулевые элементы есть не только в верхнем треугольнике, но и в примыкающей к нему побочной диагонали, то есть 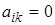при )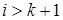

в) квазидиагональные;

г) ящичные (клеточно-диагональные), и тому подобное:

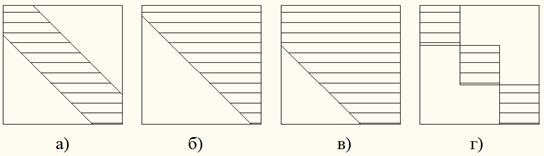
При обходе нулевых элементов решение системы с почти треугольной

матрицы (б) требует всего 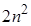действий, а с ленточной даже 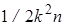, то есть выигрыш во времени очень велик, однако выбор наибольшего элемента делать нельзя, так как перестановка столбцов нарушает специальную структуру матриц; более того, в симметричных матрицах недопустим даже выбор главного элемента. Но обычно в этом нет и необходимости, так как подобные физические задачи обычно хорошо обусловлены с большими элементами на главной диагонали, для которых ошибки округления в методе Гаусса невелики.

Наиболее важным частным случаем метода Гаусса, является метод

прогонки, применяемый к системам с трехдиагональной матрицей, которые часто встречаются в краевых задачах для дифуравнений второго порядка. Трехдиагональной является ленточная матрица, у которой ненулевые элементы имеются только на главной диагонали и примыкающих ней двух побочных диагоналей, то есть 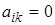при 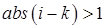(ширина ленты 3 элемента).

Такие системы записывают в каноническом виде

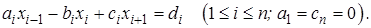(2.16)

Формула (2.16) называется разностным уравнением 2-го порядка, или

трехточечным уравнением. В этом случае прямой ход алгоритма Гаусса (без выбора главного элемента) сводится к исключению элементов 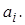Получается треугольная система, содержащая в каждом уравнени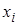и и 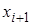, поэтому обратный ход имеет вид

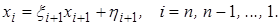(2.17)

Уменьшим в (2.17) индекс на 1 и подставим в уравнение (2.16)

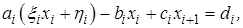
откуда

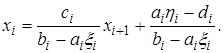
Чтобы это выражение совпало с (2.17), необходимо, чтобы его дроби были

равны соответственно 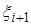и 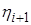. Отсюда следует удобная запись формул прямого хода

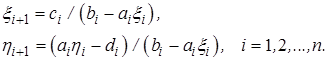(2.18)

Попутно легко находится определитель исходной трехдиагональной

матрицы

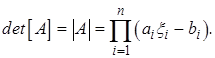(2.19) Формулы метода прогонки (2.18) и (2.17) требуют всего 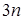ячеек памяти и 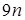действий, т.е. гораздо экономичнее метода исключений в чистом виде.

Примечания:

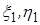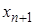1) Для начала счета удобно принять и , которые формально неизвестны, равными нулю;

2) Если выполнено условие преобладания диагональных элементов по модулю

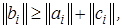(2.20)

то в формулах прямого хода (2.18) не возникает деления на нуль и тем самым исходная система (2.16) имеет единственное решение и устойчива относительно ошибок округления. Для хорошо обусловленных систем типа (2.16) прогонка достаточно устойчива даже при нарушении условия (2.20).

Метод квадратных корней применим только для линейных систем с

эрмитовой матрицей 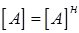(то есть 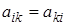; эрмитова матрица с вещественными элементами является симметричной). Метод основан на представлении исходной эрмитовой матрицы в виде произведения трех матриц

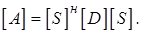(2.21)

Здесь:

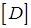- диагональная матрица с элементами на главной диагонали 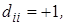то есть ,

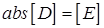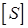- верхняя треугольная матрица ( 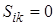при ),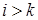

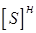- эрмитово сопряженная с ней нижняя треугольная матрица.

Для полной определенности разложения потребуем вещественности и

положительности диагональных элементов матрицы 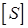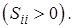Развернув (2.21) по правилам п. 1.1 для 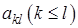, получим формулы для элементов матриц 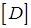и 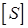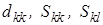, причем для диагональных элементов матрицы 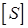выражение будет под знаком радикала, что породило название метода.

Когда для всех 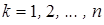все элементы матриц найдены, то решение

линейной системы 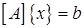сводится к последовательному решению трех систем (двух треугольных и одной диагональной):

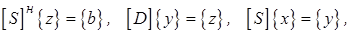(2.22)

что делается обычным обратным ходом. При необходимости вычисляется определитель матрицы

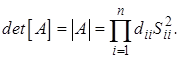(2.23)

Метод квадратных корней требует меньше памяти и вдвое быстрей метода Гаусса, что понятно, так как метод использует информацию о симметрии матрицы.

Подчеркнем, что для ленточной, ящичной и некоторых других симметричных структур матрицы матрица будет иметь аналогичную структуру, то есть содержать массивы нулевых элементов на заранее известных местах. Это, как и в методе Гаусса, позволяет сильно сократить объем вычислений. Однако для узких лент, особенно трехдиагональных, метод квадратных корней по скорости может быть в принципе даже медленнее метода Гаусса и тем более метода прогонки (из-за извлечения корней - очень медленной компьютерной операции).

Примечания:

1. Если эрмитова матрица 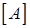вещественная и симметричная, то никаких комплексных чисел при вычислениях не возникает, и матрица 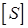также вещественная. Если к тому же матрица 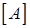положительно определенная (см. п.1.1), то есть все ее главные миноры положительны, то все 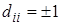, и формулы для вычисления элементов матрицы 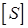могут быть несколько упрощены.

2. Метод квадратных корней эффективен и часто применяется для численного решения интегральных уравнений типа Фредгольма с симметричным ядром, так как эти задачи сводятся к линейной системе с симметричной матрицей, причем при регуляризации таких задач симметрия матрицы сохраняется /3/.