Тұзақ ангармонизмінің екіатомдық молекулалардың пайда болу жылдамдығына әсерін зерттеу

[13, 31] жұмыстарында бөлінген энергияны пайда болған молекулалардың массалар орталығының қозуына беретін екікомпонентті атомдық тұзақтағы молекулалардың резонанстық пайда болу механизмі ұсынылды.

Массалар орталығы тербелісінің қозуына салыстырмалы әсерлесудің энергиясын ''қотару'' есеп гамильтонианында араласу операторы болған кезде мүмкін болады. Бірдей атомдар жағдайында гамильтонианда мұндай қосылғыш болмайды, алайда тұзақ ангармонизмімен шартталған қосылғышын ескеру ұқсас эффектке әкеледі – пайда болған молекулалардың массалар орталығы тербелістерінің қозуына бөлінген энергия беріп, атомдық тұзақта молекулалардың резонансты пайда болуы.

Бұл механизмді зерттеу үшін бастапқы шарты төмендегідей болатын стационар емес (2.1.3) теңдеуін интегралдау қажет болады:

(2.2.1)

Ол бірі-бірінен қашықтықта болатын тұзақтың негізгі күйіндегі екі әсерлеспейтін атом болып табылады. Бұл толқындық пакет оң салыстырмалы атомаралық жылдамдықпен шашырау аймағына қозғалып барады, ол жерде шашырағаннан кейін қарама-қарсы бағытта қозғалатын екі бөлікке ыдырайды.

Резонанстық шарттарды орындау кезінде массалар орталығының қозуымен екіатомдық жүйенің (екіатомдық молекуланың) байланысқан күйіне ауысу мүмкін болады.

Осындай ауысудың ықтималдығын сандық зерттей отырып,

(2.2.2)

(мұндағы ) – массалар орталығының қозған күйін модельдейтін осцилляторлардың қозған күйінің толқындық функциялары), кезінде осы резонанстық механизмнің оңтайландыру шарттарын зерттеуді жоспарлаймыз. Бұл зерттеулер тәжірибелерді жоспарлау және интерпретациялау үшін өзекті болып табылады [7].

ПСЕВДОПОТЕНЦИАЛДЫҚ МОДЕЛЬДЕ АНГАРМОНИКАЛЫҚ ОПТИКАЛЫҚ ТҰЗАҚТАҒЫ ЕКІБӨЛШЕКТІ КВАНТТЫҚ ЖҮЙЕНІҢ ЭНЕРГЕТИКАЛЫҚ СПЕКТРІ

Оптикалық тұзақтағы псевдопотенциалдық әсерлесуімен кванттық жүйенің энергия деңгейлерін есептеу қателіктерін бағалау

Ары қарай екіөлшемді ангармонизмді есептеу үшін есептеу қателіктерін дұрыс бағалау мүмкіндігіне ие болу керек. Ол үшін біздің сандық сызбадағы қателік бағасын ангармонизм жоқ кездегі нақты бағамен (Буштың нақты нәтижесімен салыстыру кезінде алынған) салыстырамыз [31].

Сызбамыздың дәлдігін жақсарту үшін Ричардсонның экстраполяциясын қолданып көрейік, бірақ бағдарлама торы шектеулі екенін ескерте кетейік. Бұл шамамен өлшемі 300x300. Алайда, алынған нәтижелерден экстраполяцияны қолдану әрқашан да ең жақсы дәлдік бере бермейтіні байқалған; кейде дәлдік стандарты схемадан да нашар болады (ары қарай 2-кестеден көріңіз).

Ричардсон экстраполяциясы үш әртүрлі қадамдары бар есептеулер нәтижелері арасындағы белгілі бір қатынастар кезінде болады, бізде [31] есептегіш сызба бар, оның нәтижесі :

(3.1.1)

мұндағы E(0) – нақты нәтиже, яғни ретті сызбаның қателігі. Дәлдікті жақсарту үшін әртүрлі үш қадаммен үш есептеу жүргізейік - ( ) сонымен қатар [30] нәтижені мына түрде көрсетейік

(3.1.2)

Сызбаны бағалау үшін р шамасын анықтау керек. Ол үшін алынған үш теңдеулер жүйесінен қарапайым жолмен анықталады:

(3.1.3)

Енді A-ны анықтау қажет, ол екі теңдеулер жүйесінен анықталады:

(3.1.4)

A-ны анықтап және (2)-ге қойып, Ричардсон формуласын аламыз:

(3.1.5)

Есептеулер нәтижесі келесі 2-кестеде келтірілген.

Көк торда сан жоқ, өйткені берілген қадамда (яғни h) бұл күй үшін сәйкес нәтиже табылмады. Сұр торда p шамасының есептелмейтіні табылады, өйткені (3.1.3) өрнек алымындағы логарифм аргументі теріс шама болып табылады. Мұнда - кері шашырау ұзындығы.

Kесте 3 – h әртүрлі қадамында алынған сандық есептеу нәтижелері және

экстраполяция әдісімен алынған мәндер.

9-қатарда

(3.1.6)

10-қатарда

(3.1.7)

11-қатарда

(3.1.8)

12-қатарда

(3.1.9)

формулалар есептелді. Сары қатарларға назар аударайық, оларда қателіктердің сандық бағалары нақты бағалармен салыстырылады. Нақты бағалардан көрініп тұрғандай, Ричардсон экстраполяциясы стандартты сызба есебіне, яғни E(r²h) схемасына қарағанда әр кезде ең жақсы дәлдік бере бермейді.

Сондай-ақ Ричардсон сызбасы және E(r²h) стандартты сызбасының қателіктерін сандық бағалау әрқашан дерлік нақтыға қарағанда үлкен қателік беретіні бақыланады. Сұр торлар аймағында Ричардсон схемасы үшін 1/a=1 кезінде E_0,2 энергиясын есептеу кезінде ерекшелік байқалады (осы кестенің мәліметтері бойынша). Осылайша, ангармонизмді есептеу кезінде ешқандай тосын жайттар болмаса, берілген сандық бағалар сонда да жұмыс істейді.

Энергияның төмендеуі аймағында есептеулердің бұзылуы байқалады. Дәлірек айтқанда: негізгі күй үшін оң 1/а аймағы қол жетімсіз болады; E_0,2 күйлер үшін де оң 1/а аймағына жақындаған кезде дәлдіктің нашарлауы байқалады. Алайда ангармонизмнің дұрыс есептелуі үшін қолайлы аймақ жеткілікті.

Екіатомды жүйенің спектріне тұзақ ангармонизмінің әсерін есептеу үшін мына түрдегі гамильтониан қарастырылады:

(3.1.10)

Осы гамильтонианды қолдана отырып, ШТ сандық әдіспен шешіледі.Сандық әдіспен және ауытқу теориясы әдісімен алынған шешімдер 8- және 9-суреттерде графиктер түрінде көрсетілген. 8-суретте әртүрлі параметрлер мәндері үшін λ: λ=0,025; 0,05; 0,1;0,15 спектрлер алынды.

Тұтас қара қисықтар, яғни E_num – гармоникалық тұзақ үшін сандық есептеулер, E_num – әртүрлі нөлдік емес λ мәндері кезіндегі сандық есептеулер, E_pert – ауытқу теориясы бойынша есептеулер.

Cурет 11 – Екібөлшекті кванттық жүйе спектріне ангармонизм эффектісінің әсері

Тұтас қара қисықтар, яғни E_num – гармоникалық тұзақ үшін сандық есептеулер, E_num – әртүрлі нөлдік емес λ мәндері кезіндегі сандық есептеулер, E_pert – ауытқу теориясы бойынша есептеулер.

Cурет 12 – Екібөлшекті кванттық жүйе спектріне ангармонизм эффектісінің әсері

гамильтонианын қарастырып және сандық әдіспен және ауытқу теориясы бойынша шешіп, спектрлердің -1/g тіркелген мәндері үшін λ параметрлерінен тәуелділігін тұрғызайық, нәтижесі 10-суретте көрсетілген. Мұнда функцияның сол жақ шегі (яғни теріс λ<0 аймақтары) λ кеміген кезде энергия тосқауылдан асып кететіндігімен шартталған. Мұнда сандық әдіспен алынған спектрлер көк түспен және ауытқу теориясы әдісімен алынғандары қарамен құрылған.

Cурет 13 – Әртүрлі -1/g әсерлесу тұрақтылары кезіндегі энергияның λпараметрінен тәуелділігі

Cурет 14 – екібөлшекті кванттық жүйе спектріне ангармонизм эффектісінің әсері. Әртүрлі λ=0;3;-0,025 параметр мәндері үшін энергиялар тұрғызылған және n=0; n=2 үшін екі жағдай қарастырылады

Жан-жақты талдау үшін салыстырудың басқа түрін қолданайық. Мұндағы E_analytic –λ=0 жағдайындағы Буштың есептеуі. Мұнда сандық әдіспен алынған спектрлер көкпен, ауытқу теориясы әдісімен алынғандары қызылмен және Буштың есебі қарамен белгіленген.

-1/g= - 3 кезде есептеу жүргізейік. Бұл λ=0.1 үшін жағдай: 12 суретте есептеулер нәтижелері көрсетілген, берілген потенциал үшін толқындық функция құрылған.

EIG^Busch – гармоникалық тұзақтың жуықтауында орындалған есеп, EIG - -1/g=-3, λ=0.1 кездегі сандық есеп. Қара қисық – ангармоникалық тұзақ графигі, көк қисық – -1/g=-3, λ=0.1 кездегі сандық есептің толқындық функциясы.

Cурет 15 – -1/g=-3; λ=0.1 болған кездегі есептеу нәтижелері

λ=-0.07 жағдай. Нәтиже 13-суретте көрсетілген.

16 сурет – -1/g=-3; λ=-0.07 жағдай үшін есептеулер нәтижесі:

Мұнда EIG^Busch – гармоникалық тұзақ жуықтауында орындалған есеп, EIG – -1/g=-3, λ=0.1 болған кездегі сандық есептелу. Қара қисық – ангармоникалық тұзақ графигі, көк қисық – -1/g=-3, λ=-0.07 болған кездегі сандық есептің толқындық функциясы.

Теріс λ кезінде тұзақ потенциалы тосқауылмен құрылады:

(3.1.11)

мұндағы – потенциалдың максимум нүктесі. λ=-0.07 мысалында бұл 14-суреттегідей көрінеді:

EIG^Busch – гармоникалық тұзақ жуықтауында орындалған есеп, EIG – ангармоникалық тұзақтың сандық есебі. Қызыл қисық – сандық есептеулерде қолданылатын ангармоникалық тұзақ потенциалы, пунктирлі қисық – нақты ангармоникалық тұзақ, сұр қисық – гармоникалық тұзақ.

Cурет 17 – λ=-0.07 кездегі есептеу нәтижелері

ОРЫТЫНДЫ

Диссертация іске асырылуы кезінде есептеу физикасы мен азденелі жүйелер физикасының соңғы жетістіктері және де атомдық ядро мен элементар бөлшектер физикасының кейбір әдістері қолданылды. Айнымалылары ажыратылған кванттық екі дене есебі (түрлі конфигурациялы оптикалық тұзақтағы ультрасуық атомдарды дұрыс сипаттау үшін) қиын әрі маңызды болғандықтан, бұл жұмыс шеңберінде ұсынылып отырған әдістер бұл мәселені шешу үшін тиімді. Жұмыстың маңызды мәселесі тұзаққа қамалған қосатомды жүйелердің айнымалыларын ажыратуға себепші оптикалық тұзақ ангармонизмі әсерін сандық сипаттау болып табылады және өзінің өзектілігімен ерекшеленеді. Бұл мәселе екі өзекті тәсілдеме: осцилляторда өрнектелу [16] және төрт өлшемді Шредингер теңдеуі үшін арнайы сандық әдіс шеңберінде зерттелді.

Жұмыс геометриясы шектеулі ультрасуық атомдар мен молекулалардың түрлі процестерінде пайда болатын кішіөлшемді, азденелі кванттық жүйелерді теоретикалық зерттеуге бағытталған. Ультрасуық атомдар мен молекулалар физикасы қазіргі таңда ғылыми зерттеулердің ішінде кең дамып келе жатқан сала. Соңғы жылдары кішіөлшемді кванттық жүйелер мен аса коррелирленген көпбөлшекті жүйелерді зерттеу үшін бірегей эксперименттік мүмкіншіліктер осы әсерлі нәтижелер арқасында ашылуда. Оптикалық тұзақтарда жеке атомдар мен молекулаларды басқару мүмкіншілігі көрсетілген. Бұл жұмыста оптикалық тұзақ ангармонизмінің қосатомды жүйелер спектріне әсері қарастырылды. Зерттеулер осцилляторда өрнектелу әдісімен жүргізілді [17]. Бұл әдіс бұрыннан үшбөлшекті кванттық жүйелер мен сыртқы өрістегі атомдар үшін қолданылуда. Бұл әдісті екібөлшекті, кейіннен тіпті үшбөлшекті кванттық жүйелер үшін геометриясы шектеулі ангармоникалық тұзақтарға қолданылуын дамыттық [13-15]. Сонымен қатар оптикалық тұзақтағы екібөлшекті атомдық жүйелер үшін стационар емес Шредингер теңдеуін интегралдау арқылы сандық зерттеу тәсілдерін жақсарттық.

Диссертацияның бірінші бөлімінде бірөлшемді гармоникалық тұзақтағы екібозонды байланысқан жүйені сипаттайтын ШТ негізгі күйінің энергиясы кері шашырау ұзындығының функциясы ретінде есептелді. Алынған 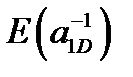тәуелділік псевдопотенциалдық әдісте орындалған есептеуден бірқатар ерекшеленеді [21]. Біздің жағдай Гаусстың реалистік потенциалын қолданумен ерекшеленеді, оны таңдау орынды болып табылады, өйткені ол атомдарда қандай да бір құрылымның бар екенін ескереді. Сондай-ақ соңғы радиус потенциалынан дельта-функция потенциалына ауысу айтарлықтай жуықтау болып табылады. Осыған ұқсас үшөлшемді шынайы потенциалмен және нөлдік радиустың псевдопотенциалымен орындалған есептеулердің салыстырылуы екіөлшемді гармоникалық тұзақ үшін [30] жұмысында келтірілген.Осциллятордаөрнектелу әдісін әсерлесу потенциалы параметрлерінің функциясы ретінде қолданылу аймағы анықталды. ОӨ әдісінің сандық есептеуден ауытқуы осцилляторлық ТФ гаусстық түрінің шынайы ТФ түрінен ауытқуымен түсіндіріледі. ОӨ әдісінің қолданылу аймағын анықтау келешекте ангармоникалық тұзақтағы екіатомды жүйе спектрін есептеу кезінде қажет болды. Қорытындылай келе, гармоникалық үшөлшемді оптикалық тұзақта қысқаәсерлі әсерлесу потенциалы бар екіатомдық жүйе спектрі осы потенциалдағы шашырау ұзындығына байланысты есептелді.

Келесі бөлімде тұзақтың ангармонизм эффекттерінің салыстырмалы қозғалыс және массалар орталығы айнымалыларының бөлінбеуіне әкелетін екібөлшекті кванттық жүйе спектріне әсерін зерттеу үшін біз квазипотенциалдық модель өңдедік. Бұл әдісте V(x) атомаралық әсерлесу g тұрақтысы бар псевдопотенциалмен бейнеленеді, ол әртүрлі ультрасуық процестер динамикасына сай сипаттайды. Бұл әдіс пайда болған екіөлшемді Шредингер теңдеуін ақырғы айырмалар әдісі көмегімен сандық зерттеуге мүмкіндік берді. Есептеулердің бұл кезеңінде екі өлшемді және үшөлшемді оптикалық тұзаққа қамалған қосатомды молекулалардың спектр сызықтар кеңеюінің тұзаққа әсерін зерттеу мақсатында квази-бірөлшемді және үшөлшемді оптикалық тұзақта энергия деңгейлерін кеңейтуді есептеу үшін бағдарлама жазылды. Бұл бағдарлама гармоникалық тұзақтың шектелген геометриясында атомдардың соқтығысуы кезіндегі шашырау параметрлерін есептеуге бағытталған, сондай-ақ басқа маңызды мәселені зерттеуге мүмкіндік береді – тұзақ ангармонизмінің тұзақтағы молекулалық (екіатомдық молекулалар) және атомдық спектрлерге әсерін зерттеу және оның түрленулері төменөлшемді кванттық есептерді мөлшерлік талдау үшін қолданылды [31].

Үшінші бөлімде псевдопотенциалдық модельде ангармоникалық оптикалық тұзақтағы екібөлшекті кванттық жүйенің энергетикалық спектрі зерттелді. Тұзақ ангармонизмі әсерін ескеру арқылы бірөлшемді геометриясы бар қосатомды жүйелер спектрі есептелді: екіөлшемді және үшөлшемді оптикалық тұзақтың ангармонизмінің әсерін есептеу үшін компьютерлік бағдарлама жазылды. Құрастырылған есептегіш сызба және оның түрленулері жұмыс мәселелері аясында зерттелетін төмен өлшемді кванттық есептерді мөлшерлі талдау үшін қолданылды. Негізгі және қозған күйлер үшін ауытқу теориясы аясында ангармоникалық түзету ескеріліп, энергетикалық спектр анықталды.