Расчет функционального преобразователя с использованием степенных зависимостей
ГЛАВА 1. ЗАДАНИЕ НА КУРСОВОЙ ПРОЕКТ
Эта глава содержит задание на курсовой проект, который выполняется по разработке микроэлектронного устройства, структурная схема которого приведена на рис. 1.1.
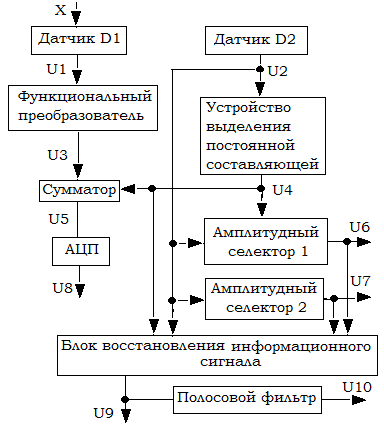
Рис. 1.1. Структурная схема системы сбора и обработки информации
Разработать функциональный преобразователь
Разработать два варианта функционального преобразователя сигнала датчика D1:
· используя гладкую аппроксимацию;
· используя кусочно-линейную аппроксимацию.
Максимальное значение напряжения на выходе функционального преобразователя U1 = 1 В.
Характеристика датчика D1 приведена в табл. 1.1.
Таблица 1.1
| Х → Вар. № ↓ | Входные данные Х первого датчика 0 1 2 3 4 5 6 7 8 9 10 ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ Выходной сигнал первого датчика U1 |
| 0 0,61 0,80 0,87 0,91 0,94 0,96 0,97 0,98 0,99 1,00 | |
| 0 0,60 0,79 0,86 0,90 0,93 0,95 0,96 0,97 0,99 1,00 | |
| 0 0,58 0,77 0,85 0,89 0,92 0,94 0,96 0,97 0,99 1,00 | |
| 0 0,57 0,79 0,86 0,91 0,94 0,97 1,00 1,03 1,04 1,05 | |
| 0 0,56 0,80 0,88 0,95 0,99 1,03 1,05 1,06 1,07 1,08 | |
| 0 0,50 0,62 0,70 0,76 0,81 0,86 0,90 0,94 0,97 0,99 | |
| 0 0,51 0,63 0,70 0,74 0,79 0,83 0,85 0,88 0,90 0,91 | |
| 0 0,52 0,80 0,96 1,04 1,08 1,12 1,15 1,17 1,19 1,20 | |
| 0 0,85 0,98 1,04 1,08 1,11 1,14 1,16 1,18 1,19 1,21 | |
| 0 0,85 1,00 1,07 1,12 1,16 1,20 1,23 1,26 1,27 1,28 | |
| 0 0,45 0,57 0,62 0,66 0,70 0,73 0,75 0,77 0,7 0,80 | |
| 0 0,50 0,59 0,65 0,69 0,71 0,72 0,75 0,76 0,77 0,79 | |
| 0 0,55 0,77 0,87 0,93 0,98 1,01 1,04 1,06 1,07 1,08 | |
| 0 0,85 1,10 1,21 1,26 1,30 1,33 1,35 1,36 1,37 1,40 | |
| 0 0,90 1,15 1,26 1,31 1,33 1,37 1,39 1,40 1,41 1,42 | |
| 0 0,95 1,20 1,27 1,32 1,34 1,38 1,40 1,41 1,42 1,43 | |
| 0 1,20 1,41 1,48 1,52 1,56 1,59 1,61 1,63 1,64 1,65 | |
| 0 0,90 1,07 1,16 1,20 1,22 1,24 1,26 1,27 1,28 1,29 | |
| 0 1,20 1,50 1,60 1,67 1,70 1,73 1,75 1,77 1,79 1,80 | |
| 0 1,20 1,55 1,70 1,78 1,83 1,87 1,90 1,92 1,93 1,94 | |
| 0 0,30 0,41 0,49 0,54 0,59 0,6 0,67 0,71 0,75 0,79 | |
| 0 0,48 0,71 0,88 0,96 1,02 1,06 1,08 1,10 1,11 1,12 | |
| 0 0,58 0,81 0,90 0,97 1,03 1,07 1,09 1,11 1,12 1,13 | |
| 0 0,81 1,10 1,25 1,34 1,40 1,44 1,46 1,48 1,49 1,50 | |
| 0 0,80 1,17 1,34 1,43 1,50 1,55 1,57 1,58 1,59 1,60 | |
| 0 0,79 1,15 1,30 1,39 1,43 1,45 1,46 1,47 1,48 1,49 | |
| 0 0,50 0,73 0,83 0,90 0,95 0,98 1,01 1,03 1,05 1,07 | |
| 0 0,53 0,81 0,97 1,05 1,09 1,13 1,16 1,18 1,20 1,22 | |
| 0 0,46 0,58 0,63 0,67 0,71 0,74 0,76 0,78 0,80 0,82 | |
| 0 0,86 1,11 1,22 1,27 1,31 1,34 1,38 1,40 1,42 1,44 | |
| 0 1,10 1,40 1,48 1,53 1,57 1,60 1,62 1,64 1,65 1,66 | |
| 0 1,11 1,58 1,71 1,79 1,84 1,88 1,91 1,93 1,94 1,95 |
Рассчитать элементы схемы датчика D2
Схема датчика D2 приведена на рис. 1.2. На рис. 1.3 приведены сигналы U2 и U2i на выходе датчика. Датчик (рис. 1.2) должен генерировать сигнал U2 (U2i) согласно табл. 1.2.
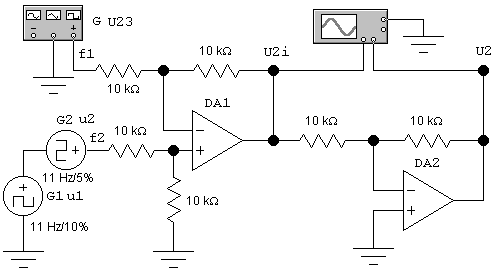
Рис. 1.2. Принципиальная схема датчика D2 (1-й вариант)
Таблица 1.2
| № вар. | G G1 G2 f1 U23 f2 % U21 f2 % U22 | № вар. | G G1 G2 f1 U23 f2 % U21 f2 % U22 |
| 60 1.0 6 10 4 6 5 2 70 1.0 7 10 4 7 5 2 80 1.0 8 10 5 8 5 3 90 1.0 9 10 6 9 5 3 100 1.0 10 10 7 10 5 4 110 1.0 11 10 6 11 5 4 120 1.0 12 10 7 12 5 3 130 1.0 13 10 8 13 5 4 140 1.0 14 10 9 14 5 4 150 1.0 15 10 6 15 5 3 160 1.0 16 10 7 16 5 2 170 2.0 17 10 8 17 5 4 180 2.0 18 10 8 18 5 5 190 2.0 19 10 9 19 5 6 200 2.0 20 10 8 20 5 4 210 2.0 21 10 7 21 5 5 | 15 1.0 1.5 10 5 1.5 5 3 20 1.0 2.0 10 6 2.0 5 3 85 1.0 8.5 10 7 8.5 5 3 95 1.0 9.5 10 8 9.5 5 4 220 1.0 22 10 7 22 5 3 230 1.0 23 10 7 23 5 4 240 1.0 24 10 9 24 5 7 250 1.0 25 10 8 25 5 3 260 1.0 26 10 7 26 5 4 270 1.0 27 10 9 27 5 5 280 1.0 28 10 7 28 5 3 290 1.0 29 10 8 29 5 4 300 1.0 30 10 7 30 5 3 310 1.0 31 10 9 31 5 4 320 1.0 32 10 7 32 5 3 330 1.0 33 10 6 33 5 3 |
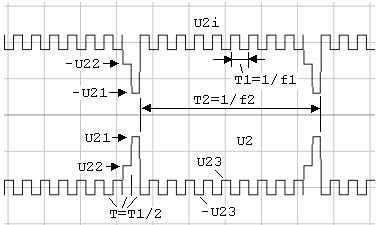
Рис. 1.3. Сигнал U2 датчика D2
Рассчитать аналоговый фильтр нижних частот
Схема фильтра приведена на рис. 1.4.Фильтр должен выделять постоянную составляющую U4 из сигнала U2 второго датчика D2. Напряжение на выходе фильтра в установившемся режиме U4 = 0,9 В при коэффициенте пульсации q2 = 0,01. Определить время переходного процесса напряжения U4.
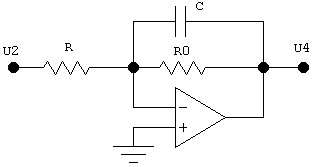
Рис. 1.4. Фильтр, выделяющий постоянную составляющую из сигнала U2
Рассчитываются следующие элементы фильтра: R, R0, C, абсолютная и относительная пульсации сигнала U4.
Разработать сумматор
Схема сумматор проведена на рис. 1.5. Напряжение на выходе сумматора U5 = U3 + U4. При напряжениях U3 = -1,0 В и U4 = -0,9 В напряжение U5 = 1,9 В, когда Ua = 0. В сумматоре предусмотреть смещение выходного напряжения U5 напряжением Ua = ±N·10 мВ, где N – номер варианта. Рассчитать величины резисторов сумматора и построить зависимости напряжения смещения Ua и U5 от величины резистора R3.
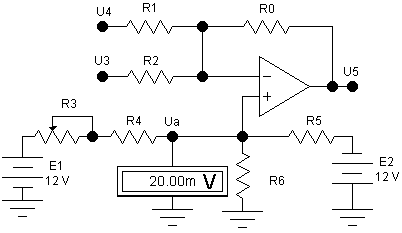
Рис. 1.5. Схема сумматора
Составить принципиальную схему устройства
ГЛАВА 2. РАСЧЕТ ПУНКТОВ ЗАДАНИЯ
Расчет функционального преобразователя
Расчет функционального преобразователя с использованием степенных зависимостей
В табл. 1.1 заданы функции первого датчика. Данные функции нельзя воспроизвести «точно» уравнением в явной или неявной форме. Для непрерывной аппроксимации функции используют логарифмические, экспоненциальные или степенные зависимости. При выполнении пункта 1.1.1 использовать степенные зависимости. Предварительно необходимо построить характеристику функционального преобразователя. На рис. 2.1 показан метод графического построения характеристики функционального преобразователя U3=f(U1).
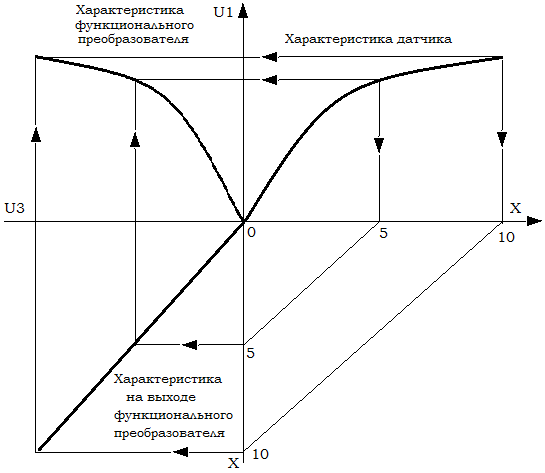
Рис. 2.1. Графическое построение характеристики функционального преобразователя
Задаемся произвольными точками на характеристике функционального преобразователя (рис. 2.2):
T1: U1=0, U3=0;
T2: U1=1,2 B, U3=0,75 B;
T3: U1=2,0 B, U2=2,25.
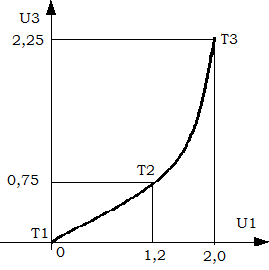
Рис. 2.2. Характеристика функционального преобразователя
Аппроксимируем характеристику функционального преобразователя при помощи полинома второй степени
U3 = U + A∙U1 + B∙(U1)2.
Составим систему уравнений
U = 0;
1,2∙A + 1,44∙B = 0,75;
2,0∙A + 4,0∙B = 2,25.
Решив эту систему относительно B и С, получим
A = -0,125, B = 0,625.
Следовательно,
U3 = -0,125∙U1 + 0,625∙(U1)2.
Данное уравнение реализуется схемой, приведенной на рис. 2.3
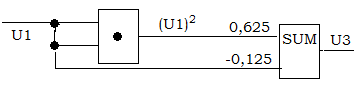
Рис. 2.3. Схема реализации функционального преобразователя
полиномом второй степени
Схема состоит из умножителя и сумматора (SUM).
Характеристику функционального преобразователя можно реализовать при помощи полинома третьей степени (рис. 2.4)
U3 = U + A∙U1 + B∙(U1)2 + C∙(U1)3.
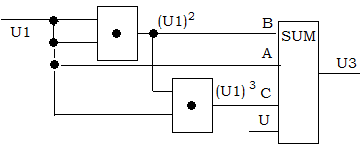
Рис. 2.4. Схема реализации функционального преобразователя
полиномом второй степени
Если рассмотренные методы дают значительную погрешность воспроизведения функции, то можно использовать метод наименьших квадратов для полинома второй или третьей степени. Для квадратичного уравнения коэффициенты A, B и C можно найти, решая систему:
A∙n + B∙∑U1 + C∙∑(U1)2 = ∑U3,
A∙∑U1 + B∙∑(U1)2 + C∙∑(U1)3 = ∑U3∙U1,
A∙∑(U1)2 + B∙∑(U1)3 + C∙∑(U1)4 = ∑U3∙(U1)2,
где n – количество заданных точек (согласно табл. 1.1).
Для определения сумм, необходимых при вычислении коэффициентов A, B и С, составляем таблицу 2.1.
Таблица 2.1
| N | U1 | U3 | U1∙U3 | (U1)2 | (U1)2∙U3 | (U1)3 | (U1)4 |
| ∑ | 0,000 0,100 0,200 0,300 0,400 0,500 0,600 0,700 0,800 0,900 1,000 5,500 | 0,010 0,020 0,060 0,140 0,230 0,340 0,460 0,600 0,720 0,860 1,000 4,440 | 0,000 0,002 0,012 0,042 0,092 0,170 0,276 0,420 0,576 0,774 1,000 3,364 | 0,000 0,010 0,040 0,090 0,160 0,250 0,360 0,490 0,640 1,000 3,850 | 0,000 0,000 0,002 0,013 0,037 0,085 0,166 0,294 0,461 0,697 1,000 2,754 | 0,000 0,001 0,008 0,027 0,064 0,125 0,216 0,343 0,512 0,729 1,000 3,025 | 0,000 0,000 0,002 0,008 0,026 0,063 0,130 0,240 0,410 0,656 1,000 2,533 |
По значениям сумм, взятых из табл. 2.1, составляем систему уравнений
11∙A + 5,5∙B +3,85∙C = 4,44,
5,5∙A + 3,85∙B + 3.025∙C = 3,364,
3,85A + 3.025∙B + 2.533∙C = 2.754.
Для определения коэффициентов системы можно использовать метод исключения переменных.
Если ошибка воспроизведения функции полиномом второй степени получается значительной, то необходимо использовать полином третьей или четвертой степени. Коэффициенты полинома третьей степени можно получить, решая систему нормальных уравнений:
A∙n + B∙∑U1 + C∙∑(U1)2 + D∙∑(U1)3 = ∑U3,
A∙∑U1 + B∙∑(U1)2 + C∙∑(U1)3 + D∙∑(U1)4 = ∑U1∙U3,
A∙∑(U1)2 + B∙∑(U1)3 + C∙∑(U1)4 + D∙∑(U1)5 = ∑(U1)2∙U3,
A∙∑(U1)3 + B∙∑(U1)4 + C∙∑(U1)5 + D∙∑(U1)6 = ∑(U1)3∙U3.
Программа построения характеристики функционального преобразователя с использованием полинома 3-го порядка. Вектор U1 необходимо взять из табл. 1.1.
%Аппроксимация исходной функции
U1=[0 0.51 0.74 0.83 0.9 0.95 0.98 1.01 1.03 1.05 1.07];
U3=[0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1];
p=polyfit(U1,U3,3)%3-й порядок аппроксимирующего полинома
p1=polyfit(U1,U3,4)%4-й порядок аппроксимирующего полинома
U=0:0.01:1.1;
Y=polyval(p,U);
Y1=polyval(p1,U);
plot(U1,U3,'o',U,Y,'K',U,Y1,':K')
grid
Из рис. 2.5 видно, что на начальном участке имеется большая ошибка преобразователя. Для уменьшения ошибки преобразования на начальном участке характеристики функционального преобразователя добавляем контрольные точки:
%Увеличиваем количество точек
U1=[0 0.1 0.2 0.35 0.51 0.74 0.83 0.9 0.95 0.98 1.01 1.03 1.05 1.07];
U3=[0 0.02 0.04 0.06 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1];
p=polyfit(U1,U3,3)%3-й порядок аппроксимирующего полинома
p1=polyfit(U1,U3,4)%4-й порядок аппроксимирующего полинома
U=0:0.01:1.1;
Y=polyval(p,U);
Y1=polyval(p1,U);
plot(U1,U3,'o',U,Y,'K',U,Y1,':K')
grid
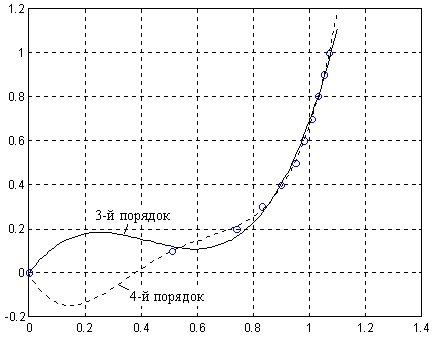
Рис. 2.5. Аппроксимация характеристики функционального преобразователя
по исходным данным
Результат расчета при наличии дополнительных точек показан на рис. 2.6.
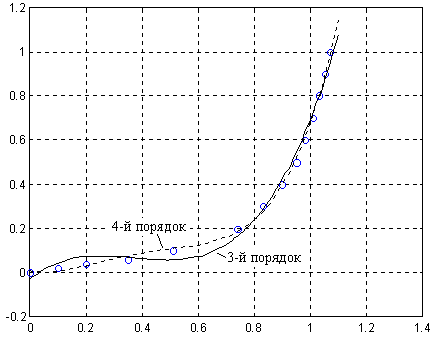
Рис. 2.6. Аппроксимация характеристики функционального преобразователя
по преобразованным данным
Коэффициенты 3-го полинома аппроксимации функционального преобразователя по преобразованным данным
p = 2.8015 –3.0965 1.0222 –0.0304.
Коэффициенты 4-го полинома аппроксимации функционального преобразователя по преобразованным данным
p1 = 3.9771 –5.9136 2.8650 –0.2551 0.0089
Более высокую точность реализации функции обеспечивает полином 4-го порядка. Уравнение реализации функции полиномом 4-го порядка имеет следующий вид:
U3 = 3.9771 U14 – 5.9136 U13 + 2.8650 U12 – 0.2551 U1.
Используя MATLAB+SIMULINK, составляем модель функционального преобразователя (рис. 2.7).
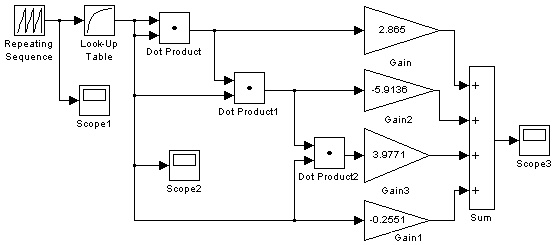
Рис. 2.7. Модель функционального преобразователя в MATLAB+SIMULINK
Настройка датчика D1 показана на рис. 2.8.
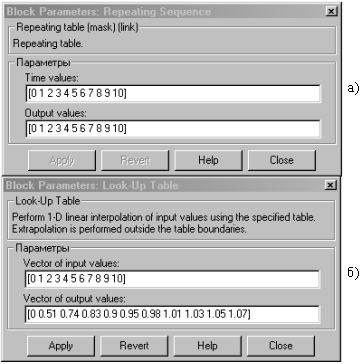
Рис. 2.8. Настройка датчика D1:
а – параметры входного сигнала Х; б – параметры датчика D1
Результат моделирования в системе MATLAB+SIMULINK приведен на рис. 2.9.
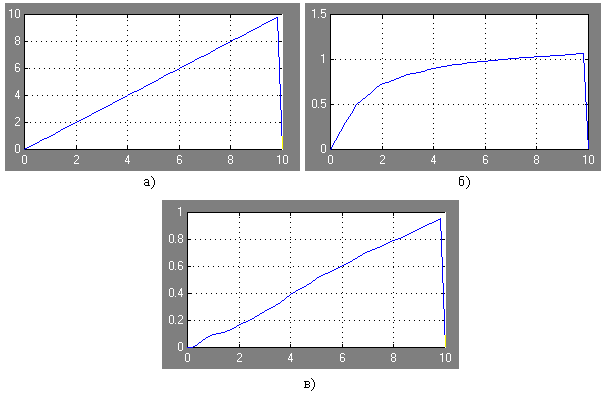
Рис. 2.9. Результат моделирования в системе MATLAB+SIMULINK:
а – входной сигнал Х датчика D1; б – сигнал U1 на выходе датчика D1;
в – сигнал U3 на выходе функционального преобразователя
С помощью программы, приведенной ниже, построим семейство характеристик элементов степенного ряда, произведем обратное преобразование и определим абсолютную ошибку функционального преобразователя:
%U3=3.9771*U1^4 -5.9136*U1^3 +2.865*U1^2 -0.2551*U1
U=0:0.01:1.07;
y4=3.9771*U.^4;
y3=-5.9136*U.^3;
y2=2.865*U.^2;
y1=-0.2551*U;
U_3=y1+y2+y3+y4;
plot(U,y4,'R',U,y3,'G',U,y2,'B',U,y1,'M',U,U_3,'K')
grid
text(1.1,5,'y4')
text(1.1,-7,'y3')
text(1.1,3.3,'y2')
text(1.1,-0.4,'y1')
text(1.1,1,'y')
U1=[0 0.51 0.74 0.83 0.9 0.95 0.98 1.01 1.03 1.05 1.07];
U3=[0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1];
yy4=3.9771*U1.^4;
yy3=-5.9136*U1.^3;
yy2=2.865*U1.^2;
yy1=-0.2551*U1;
yy=yy1+yy2+yy3+yy4;
yy11=-0.245*U1;%корректирующий элемент
yyy=yy11+yy2+yy3+yy4;
det=yy-U3;
det1=yyy-U3;
figure
subplot(2,1,1)
bar(det,0.5)
colormap(cool)
grid
xlabel('Расчетная ошибка')
subplot(2,1,2)
bar(det1,0.5)
colormap(cool)
grid
xlabel('Скорректированная ошибка')
figure
plot(U1,U3,'o',U1,yy,'*')
grid
xlabel('Данные: o - исходные; * - корректированные')
На рис. 2.10 показано семейство характеристик элементов степенного ряда.
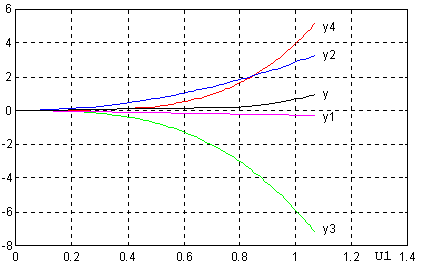
Рис. 2.10. Семейство характеристик элементов степенного ряда
Для оптимизации преобразования необходимо произвести коррекцию коэффициентов степенного ряда (рис. 2.11).
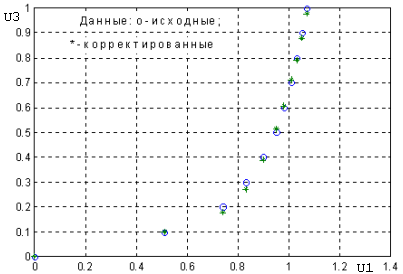
Рис. 2.11. Графики U1 = f(U3) исходного и корректированного
На рис. 2.12 показаны диаграммы абсолютной ошибки преобразования.
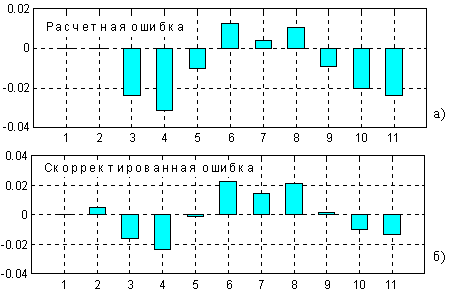
Рис. 2.12. Диаграммы абсолютной ошибки преобразования:
а – расчетная ошибка; б – скорректированная ошибка
Используя ELECTRONICS WORKBENCH, составляем модель функционального преобразователя (рис. 2.13). Определяем величины резисторов схемы:
R1 = R0/0,2551; R2 = R0/2,865; R3 = R0/5,9136; R4 = R0/3,9771.
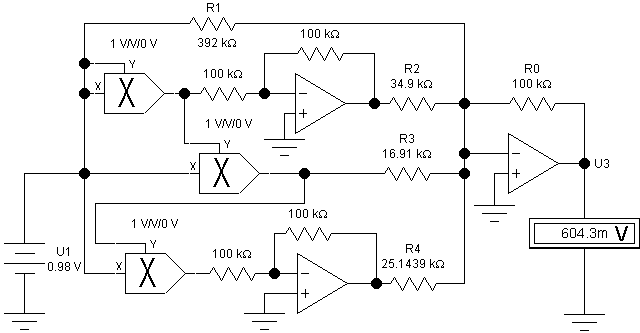
Рис. 2.13. Модель функционального преобразователя (ELECTRONICS WORKBENCH)
Результат моделирования приведен в табл. 2.1.
Таблица 2.1
| U1 В | 0 0,51 0,74 0,83 0,90 0,95 0,98 1,01 1,03 1,05 1,07 |
| U3 мВ | 0 99,8 176,5 268 389,6 512 604,3 711 791 879,5 976,5 |
