Геометрические вероятности

В §5 была рассмотрена система аксиом теории вероятностей. Конкретные реализации этой системы, возникающих при решении практических задач, могут быть различными.

Так в классической схеме (§6) рассмотрена реализация, когда пространство Ω элементарных событий есть множество, состоящее из конечного числа n элементов, причем вероятности этих элементов одинаковы. Рассмотрим ещё один наглядный пример реализации этой системы.

Пусть Ω есть некоторая область на прямой, плоскости или в пространстве. Условимся называть событиями всевозможные подмножества в Ω (которые можно измерить – т.е. найти их длину, площадь, объём). Каждому событию А поставим в соответствии его вероятность по формуле

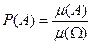, (1)

где 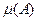обозначает меру множества А. Все аксиомы – как для событий, так и для вероятностей (см. §5) будут в этом

случае выполнены.

Особенностью этой модели является её геометрический характер: при этом существенно, что вероятности Р(А) определяются не конкретно формой множества А и его расположением в Ω , а единственно его мерой .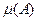

К указанной выше геометрической схеме сводится довольно большой круг задач. В каждой из них элементарные события можно трактовать как случайный выбор точки в некоторой области Ω. При этом, условия задачи должны быть такими, чтобы все точки в Ω можно было считать «равноправными» (в смысле возможности их выбора).

Отметим одно следствие в этой (геометрической) схеме, не имеющего аналога в классической схеме.

Точка ω в Ω является элементарным событием и значит, исходя из формулы (1), получаем .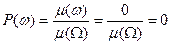

Итак, вероятности элементарных событий равны нулю. Тем не менее, эти события возможны: мы предполагаем, что можно попасть в любую точку ω области Ω.

Как можно истолковать такое явление?

В § 2 мы условились считать очень маловероятные события практически невозможными. Тем более следует считать практически невозможными события нулевой вероятности.

Итак, попадание в данную геометрическую точку ω надо рассматривать, как событие практически невозможное, хотя теоретически оно и может произойти.

В качестве примера рассмотрим следующую «задачу о встрече».

Пример. Между 12-ью часами и часом дня должен произойти в случайный момент звонок квартирного телефона, причём вызывающий ждёт 10 минут. В течение этого же часа хозяин квартиры заходит домой в случайный момент и остается дома в течение 30 минут. Какова вероятность, что разговор состоится (событие А).

Решение. Тот факт, что звонок происходит в момент у, а хозяин квартиры приходит в момент х, можно изобразить точкой плоскости с координатами (х;у); при этом будем отсчитывать х и у в минутах от 12 часов. Тогда все возможные комбинации вызова и прихода (элементарные исходы) изобразятся точками квадрата Ω: 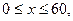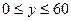(см. рис.1). Поскольку, моменты звонка и прихода случайны и не зависят друг от друга, то все точки (элементарные исходы) в квадрате можно считать равноправными (в смысле возможности их выбора). Выясним теперь, какие точки (х;у) благоприятствуют событию А («разговор состоялся»). Разговор может состояться лишь в том случае, если момент звонка не больше чем на тридцать минут раньше момента прихода и не меньше чем на 10 минут позже прихода, т.е. .

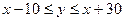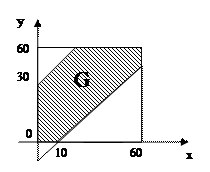
Итак, область G квадрата, благоприятствующая А, состоит из точек (х;у), координаты которых удовлетворяют

неравенствам 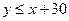, , 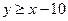то есть из точек, лежащих между прямыми (см. рис 1).

Площадь квадрата равна 3600; вычитая площади двух угловых треугольников, находим, что, площадь области G равна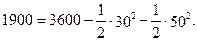

Рис.1

Отсюда получаем искомую вероятность

.

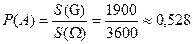Условная вероятность.