Решение уравнения c одной переменной

Задание 1

Сделать отделение корней: графически и по программе (точность 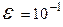). Индивидуальные задания приведены в таблице 1.

1. Определение, построение таблиц значений и графиков функций и отделение корней уравнения y=x-sinx-0,25.

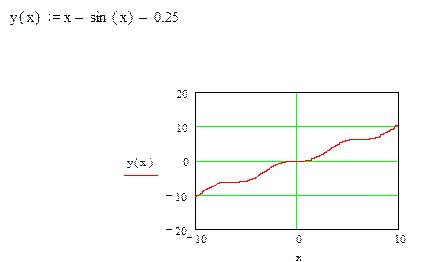Отделяем корни графически.

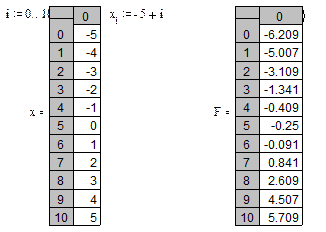Вычисляем значения аргумента и функции.

Набираем i, x_i F_i. Ниже, x= и рядом щелкаем мышью, набираем F= ,также рядом щелкаем мышью.

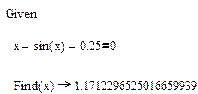2. Решение с использованием операторов given, find.

Таблица 1

N	Метод	Уравнение
	K
	К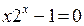
	Х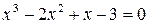
	К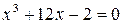
	Х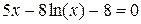
	К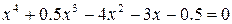
	Х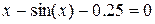
	K
	X
	K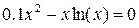

КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Этапы решения уравнения с одной неизвестной.

2. Способы отделения корней.

3. Каким образом графическое отделение корней уточняется с помощью вычислений?

4. Дать словесное описание алгоритма метода половинного деления.

5. Необходимые условия сходимости метода половинного деления.

6. Условие окончания счета метода простой итерации. Погрешность метода.

7. Словесное описание алгоритма метода хорд. Графическое представление метода. Вычисление погрешности.

8. Словесное описание алгоритма метода касательных (Ньютона). Графическое представление метода. Условие выбора начальной точки.

Лабораторная работа № 3

Решение систем линейных уравнений

Методы решения систем линейных уравнений

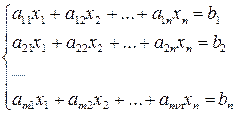(2.1)

или в векторном виде

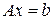(2.2)

можно разделить на две основные группы: прямые методы и итерационные. Прямые методы дают точное решение за конечное число операций; к ним относятся, например, методы Крамера и Гаусса. Итерационные методы дают решение системы уравнений как предел последовательных приближений. Для итерационных методов необходимо выполнение условий сходимости и дополнительных преобразований системы в эквивалентную ей.

Задание 1

Примерный вариант выполнения

лабораторной работы

Пример. Решите систему уравнений

X₁+2X₂+3X₃=7,

X₁-3X₂+2X₃=5,

X₁+X₂+X₃=3.

1. Символьное решение систем уравнений

Фрагмент рабочего документа с соответствующими вычислениями приведен ниже. Здесь =- логическое равенство.

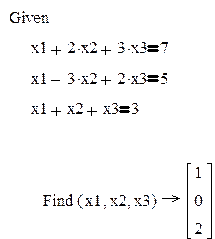2. Решение системы линейных алгебраических уравнений как матричное уравнение Ax=b

Порядок выполнения задания.

1. Установите режим автоматических вычислений.

2. Введите матрицу системы и матрицу-столбец правых частей.

3. Вычислите решение системы по формуле x=A^-1b.

4. Проверьте правильность решения умножением матрицы системы на вектор-столбец решения.

5. Найдите решение системы с помощью функции lsolve и сравните результаты.

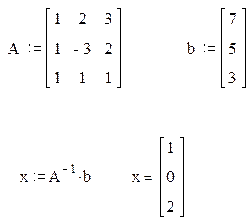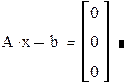Решим систему с помощью функции lsolve и сравним результат с решением x=A^-1b.

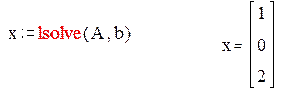Таблица 2

№ вар.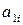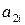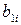
	0.35 0.12 - 0.13	0.12 0.71 0.15	- 0.13 0.15 0.63	0.10 0.26 0.38
	0.71 0.10 - 0.10	0.10 0.34 0.64	0.12 - 0.04 0.56	0.29 0.32 - 0.10
	0.34 - 0.04 0.06	- 0.04 0.44 0.56	0.10 - 0.12 0.39	0.33 - 0.05 0.28
Решение варианта 2 различными способами

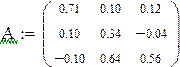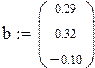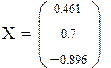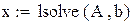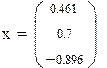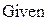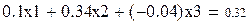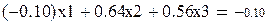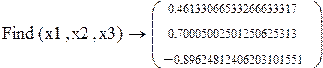КОНТРОЛЬНЫЕ ВОПРОСЫ

1. К какому типу - прямому или итерационному - относится метод Гаусса?

2. В чем заключается прямой и обратный ход в схеме единственного деления?

3. Как организуется, контроль над вычислениями в прямом и обратном ходе?

4. Как строится итерационная последовательность для нахождения решения системы линейных уравнений?

5. Как формулируется достаточные условия сходимости итерационного процесса?

Лабораторная работа № 4