Дифференциальные зависимости между внутренними усилиями при изгибе

Рассмотрим расчетную схему балки с произвольной распределенной нагрузкой (рис.2).

Составим уравнение равновесия:

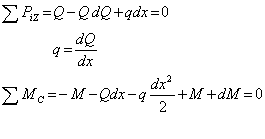
Таким образом, действительно: первая производная от внутреннего изгибающего момента по линейной координате равна поперечной силе в сечении.

Это известное свойство функции и ее первой производной успешно используется при проверке правильности построения эпюр. Так, для расчетной схемы консольной балки (рис.1) эта связь дает следующие проверочные результаты:

и М убывает от 0 до -Pl.

и М º х.

Таким образом, для квалифицированной проверки Вам рекомендуется вспомнить из высшей математики раздел, связанный с вычислением производных функции. Считаю целесообразно решить тесты, приведенные в ПРИЛОЖЕНИИ под разделом Т-3.

Рассмотрим ВТОРОЙ ХАРАКТЕРНЫЙ ПРИМЕР ИЗГИБА двухопорной балки (рис.3).

Очевидно, что опорные реакции RA = RB :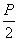

для первого участка (рис.3, б) -

для второго участка (рис.3, в) -

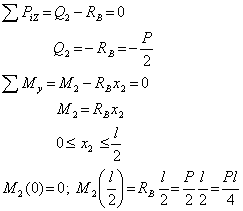
Эпюры внутренних усилий представлены соответственно на рис.3, г и 3, д.

На основе дифференциальной связи Q и М, получим:

• для первого участка:

Q > 0 и М возрастает от нуля до .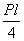

Q = const и M º x

• для второго участка:

Q < 0 и М убывает с 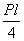до нуля.

Q = const и M также пропорционален х, т.е. изменяется по линейному закону.

Опасным в данном примере является сечение балки в центре пролета:

ТРЕТИЙ ХАРАКТЕРНЫЙ ПРИМЕР

связан с использованием распределенной по длине балки нагрузки (рис.4). Следуя методике, принятой ранее, очевидно равенство опорных реакций: 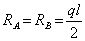, а для искомого сечения (рис.4, б) выражения для внутренних усилий приобретают вид:

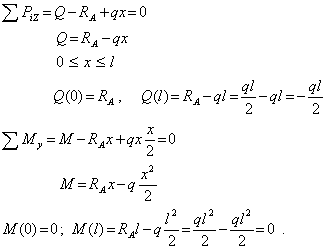
На обеих опорах изгибающий момент отсутствует. Тем не менее опасным сечением балки будет центр пролета при . Действительно, исходя из свойства функции и производной при 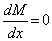, внутренний изгибающий момент достигает экстремума. Для нахождения исходной координаты х₀ (рис.3 в) в общем случае приравняем выражение поперечной силы к нулю. В итоге получим

После подстановки в выражение изгибающего момента получим:

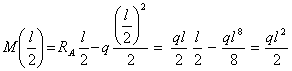
Таким образом, .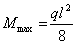

Необходимо отметить, что техника построения эпюр при изгибе наиболее трудно усваивается слушателями.

5 Понятие о напряжениях и деформациях

Ключевые слова: нормальное и касательное напряжения, линейная и угловая деформации, тензор напряжений.

Как отмечалось выше, внутренние силы, действующие в некотором сечении со стороны отброшенной части тела, можно привести к главному вектору и главному моменту. Зафиксируем точку М в рассматриваемом сечении с единичным вектором нормали n. В окрестности этой точки выделим малую площадку DF. Главный вектор внутренних сил, действующих на этой площадке, обозначим через DP (рис. 1, а). При уменьшении размеров площадки соответственно

уменьшаются главный вектор и главный момент внутренних сил, причем главный момент уменьшается в большей степени. В пределе при DF®0 получим

Аналогичный предел для главного момента равен нулю. Введенный таким образом вектор р_n называется вектором напряжений в точке. Этот вектор зависит не только от действующих на тело внешних сил и координат рассматриваемой точки, но и от ориентации в пространстве площадки DF, характеризуемой вектором n. Совокупность всех векторов напряжений в точке М для всевозможных направлений вектора n определяет напряженное состояние в этой точке.

В общем случае направление вектора напряжений р_n не совпадает с направлением вектора нормали n. Проекция вектора р_n на направление вектора n называется нормальным напряжением s_n, а проекция на плоскость, проходящую через точку М и ортогональную вектору n, - касательным напряжением t_n (рис. 1 б).

Размерность напряжений равна отношению размерности силы к размерности площади. В международной системе единиц СИ напряжения измеряются в паскалях: 1 Па=1 Н/м².

При действии внешних сил наряду с возникновением напряжений происходит изменение объема тела и его формы, т. е. тело деформируется. При этом различают начальное (недеформированное) и конечное (деформированное) состояния тела.

Отнесем недеформированное тело к декартовой системе координат Oxyz (рис. 2). Положение некоторой точки М в этой системе координат определяется радиус-вектором r(х, у, z). В деформированном состоянии точка М займет новое положение М', характеризуемое радиус-вектором r' (х, у, z). Вектор u=r'-r называется вектором перемещений точки М. Проекции вектора u на координатные оси определяют компоненты вектора перемещений u(х, у, z), v(х, у, z), w(х, у, z), равные разности декартовых координат точки тела после и до деформации.

Перемещение, при котором взаимное расположение точек тела не меняется, не сопровождается деформациями. В этом случае говорят, что тело перемещается как жесткое целое (линейное перемещение в пространстве или поворот относительно некоторой точки). С другой стороны, деформация, связанная с изменением формы тела и его объема, невозможна без перемещения его точек.

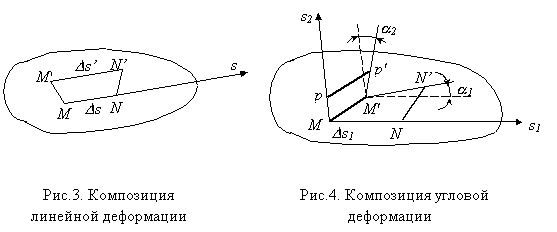
Деформации тела характеризуются изменением взаимного расположения точек тела до и после деформации. Рассмотрим, например, точку М и близкую к ней точку N, расстояние между которыми в недеформированном состоянии вдоль направления вектора s обозначим через Ds (рис. 2). В деформированном состоянии точки М и N переместятся в новое положение (точки М' и N'), расстояние между которыми обозначим через Ds'. Предел отношения

называется относительной линейной деформацией в точке М в направлении вектора s. Рассматривая три взаимно перпендикулярных направления, например, вдоль координатных осей Ох, Оу и Oz, получим три компоненты относительных линейных деформаций ex, ey, ez, характеризующих изменение объема тела в процессе деформации.

Для описания деформаций, связанных с изменением формы тела, рассмотрим точку М и две близкие к ней точки N и Р, расположенные в недеформированном состоянии в направлении двух взаимно ортогональных векторов s₁ и s₂. Расстояния между точками обозначим через Ds₁ и Ds₂ (рис. 4). В деформированном состоянии положение точек обозначим через М', N' и Р'. Угол между отрезками M'N' и М'Р' в общем случае будет отличным от прямого. При Ds₁®0, Ds₂®0 изменение угла g₁₂ между двумя ортогональными до деформации направлениями называется угловой деформацией. Как видно из рис. 4, угловая деформация складывается из двух углов a₁ и a₂, связанных с поворотами отрезков M'N' и М'Р' в плоскости, образованной векторами s₁ и s₂, относительно этих векторов. Если заданы три взаимно ортогональных вектора, направленных вдоль координатных осей, то имеются три угловые деформации g_xy, g_xz и g_yz, которые вместе с тремя линейными деформациями ex, ey и ez полностью определяют деформированное состояние в точке.