Моделирование нейтронного потока в графитовой призме

Цель работы: изучение с помощью электрической сеточной модели пространственного распределения нейтронного потока в графитовой призме

Теоретические основы

Для проведения экспериментов по определению нейтронно-физических параметров материалов, применяемых в ядерной технике, применяют призму-сборку, например, из графитовых блоков, одна грань которой облучается потоком нейтронов, создаваемым источником нейтронов или с помощью тепловой колонны. Измеряя характеристики нейтронного поля, можно определить свойства материала призмы.

Распределение нейтронного потока в призме в одногрупповом диффузионном приближении описывается уравнением:

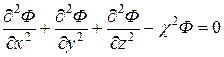, (1)

где 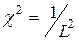; 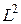– длина диффузии.

Размеры призмы с экстраполированными добавками в направлении осей x, y, z равны соответственно a, b, c (рис. 1). Плоский источник тепловых нейтронов мощностью S, нейтр./(см²×с) расположен на грани призмы в плоскости z = 0.

Поскольку моделирование распределения нейтронного потока будет проводится на двумерной сетке, в плоскости x, z, разделение переменных в исходном уравнении производится следующим образом:

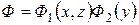, (2)

При этом уравнение (1) приводится к следующему виду:

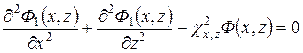, (3)

причем 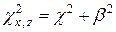. (4)

Решение уравнения (3) должно удовлетворять нулевым граничным условиям на экстраполированных границах на всех гранях призмы, кроме грани z = 0. В плоскости z = 0 задается условие источника:

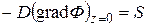, (5)

Решение уравнения, полученное методом разделения переменных, известно:

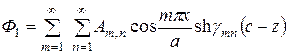, (6)

причем ; ; .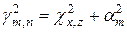

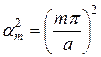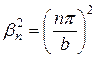В средней части призмы, т.е. на некотором расстоянии от плоскостей z = 0 и
z = c распределение потока нейтронов хорошо описывается упрощенной формулой:

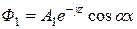, (7)

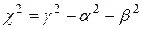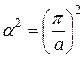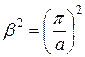причем , где ; . (8)

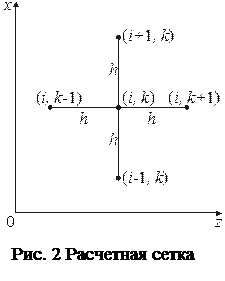
Для того, чтобы моделировать уравнение (3), его нужно представить в конечно-разностной форме, т.е. заменить дифференциальные операторы конечно-разностными. Шаг сетки при переходе к конечным разностям принимаем одинаковым по осям x и z, т. е. 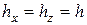(рис. 2). Переходим к безразмерной величине потока нейтронов, произвольно выбрав базисное значение потока Ф^*:

.

Уравнение (3) в конечно-разностной форме для узла (i, k) можно записать следующим образом:

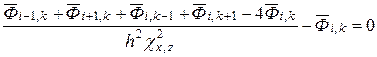, (9)

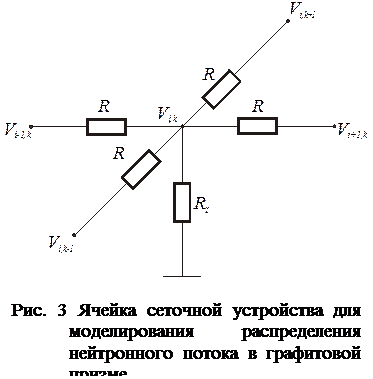где .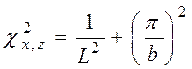

Моделирующее устройство и выбор параметров элементов этого устройства. Конечно-разностные уравнения распределения нейтронного потока в графитовой призме можно решать с помощью специализированного вычислительного устройства, содержащего сетку сопротивления. Ячейка такого сеточного устройства приведена на рис.3 Токи в сопротивлениях R моделируют процесс диффузии нейтронов, в сопротивлениях R_п – поглощение нейтронов. Уравнение баланса токов в электрической сетке для узла (i, k) имеет следующий вид:

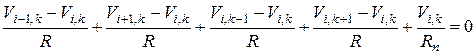, (10)

или после перехода к безразмерным величинам потенциала 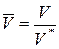, где V^*– некоторое базисное значение потенциала, получим:

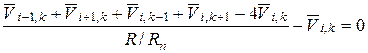. (11)

Из сравнения уравнений (9) и (10) можно получить условие моделирования, т.е. условия, при которых распределение потенциала в узлах сетки сопротивлений (модели) аналогично распределению нейтронного потока в моделируемой графитной призме. Условия моделирования:

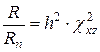. (11)

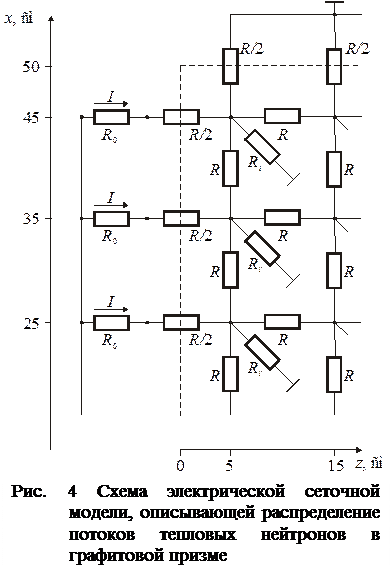
При моделировании должно быть выполнено условие источника (5). Если записать это условие в конечно-разностной форме и сравнить его с соответствующими для токов в сопротивлениях сетки на границе z=0, то получим дополнительные условия моделирования для задания токов, моделирующих источников нейтронов (рис. 4).

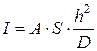. (12)

Если источник нейтронов однороден, т.е. величина S не зависит от координат, моделирование источника заключается в задании одинаковых токов I во всех ветвях. Чтобы избежать регулировки этих токов, можно задать их через большие сопротивления R₀ (рис. 4). При R₀>>R токи I будут практически одинаковы. Выполнение нулевых граничных условий обеспечивается заземления контура сетки, т.е. узлов с координатам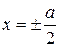и и 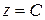. В настоящие работе моделируется графитовая призма следующих размеров: а = 100 см; b = 100 см; c = 180 см. Шаг моделирования h = 10 см. Квадрат длины диффузии в графите L²= 1164 см². Величина сопротивления в сетке: R = 2,4 ком ± 5%, R_п = 13 ком ± 5%.