Сиплексный метод оптимизации

Моделирование процессов

При изучении физических явлений применяют два метода исследований, которые позволяют получить коли­чественные закономерности для исследуемых явлений. В первом методе используют экспериментальное изучение конкретных свойств единичного явления, во вором исходят из теоретического исследования рассматриваемой проблемы.

Достоинством экспериментального метода исследования является достоверность получаемых результатов. Кроме того, при выполнении эксперимента основное внимание можно сосредоточить на изучении величин, предс­тавляющих наибольший практический интерес.

Основной недостаток экспериментального метода исследования заключается в том, что результаты данного эксперимента не могут быть использованы применительно к другому явлению, которое в деталях отличается от изученного. Поэтому выводы, сделанные на основании анализа результатов данного экспериментального иссле­дования, не допускают распространения их на другие явления. следовательно, при экспериментальном методе исследования каждый конкретный случай должен служить самостоятельным объектом изучения.

Второй метод исследования для нахождения количественных зависимостей, который широко применяется современной наукой, рассматривается в математической или теоретической физике. При выводе дифференциаль­ных уравнений теоретической физики используются самые общие законы природы, которые в свою очередь явля­ются результатом чрезвычайно широкого обобщения опытных данных, приложение этих общих законов к изучаемым явлениям позволяет получить наиболее общие связи между физическими параметрами явления. (Пример, диф. ур-ние тепл.) Обычно такие уравнения описывают целый класс явлений.под классом понимается такая совокуп­ность физических явлений, которая характеризуется одинаковым механизмом процессов и одинаковой физической природой.

При интегрировании любого дифференциального уравнения можно получитьбесчисленное множестворазличных решений, удовлетворяющих этому уравнению. Для получения из множества решений одного частного решения надо знать все характерные особенности данного явления, выделяющие его из всего класса однородных явле­ний. Эти дополнительные условия, которые вместе с дифференциальным уравнением однозначно определяют еди­ничное явление, называют условиями однозначности. Условия однозначности должны содержать все особенности данного конкретного явления. ( геометрические свойства, физические свойства, начальные условия, граничные условия).

Дифференциальное уравнение и четыре условия однозначности определяют конкретное единичное явления. В большинстве случаев из-за сложности изучаемых явлений найти решение, удовлетворяющее дифференциальным уравнениям и условиям однозначности, невозможно.

Следовательно, если недостатком экспериментального метода исследования является невозможность расп­ространения результатов, полученных в данном опыте, на другие явления, отличающиеся от изученного, то не­достатком математической физики является невозможность перейти от класса явлений, характеризуемых диффе­ренциальными уравнениями и условиями однозначности, к единичному конкретному явлению. Каждый из этих ме­тодов в отдельности не может быть эффективно использован для решения практических задач. Поэтому очень многие явления исследуются методами моделирования.

Моделированием называют метод экспериментального исследования, в котором изучение какого-либо физи­ческого явления производится на специальной модели.

Различают условное, аналоговое, математическое моделирование

Условное моделирование - это замещение сигнала условной моделью, представляющей его только благодаря определенной договоренности о смысле, приписанном этой модели.

Условными являются, прежде всего, знаковые модели. Знак или символ - это искусственный образ, чисто условно обозначающий вполне определенный объект и, как правило, не имеющий с этим объектом никакого сходства. Отдельный знак, т.е. простейшая условная модель, обладает ограниченными моделирующими возмож­ностями. Он условно обозначает вещь, явление, действие, событие, свойство, связь или отношение вещей, яв­лений, свойств и т.д.

Сформулировать общие правила построения знаковых моделей невозможно, так как формирование их всегда имеет поисковый эвристический характер. Можно только указать основные требования, которые предъявляются к этим моделям: необходимость, простота, наглядность, индивидуальность, однозначность, единообразие, опре­деленность, учет установившихся традиций.

Удачно выбранная знаковая модель получает всеобщее признание и распространение. Условными являются также образно-знаковые модели, которые отличаются наглядностью и могут обладать определенным сходством с оригиналом. Примерами удачных образно-знаковых моделей служат структурные схемы и направленные графики систем автоматического управления, наглядно показывающие число звеньев, составляющих схему, связи звень­ев, переменные величины, действующие на входах и выходах звеньев и системы в целом.

К знаковым и образно-знаковым моделям относятся все математические формы выражения количественных от­ношений между переменными и постоянными величинами. Поэтому условным моделированием приходится заниматься каждому, кто применяет математические методы при решении различных задач науки, техники, экономики и т.д.

Сравнивать те или иные объекты можно, только в том случае, если они однородны. В случае однородности объектов-оригиналов говорят и об однородности их символических моделей.

Каждый материальный объект обладает несколькими свойствами, допускающими количественное выражение. Каждое свойство характеризуется определенной физической величиной, между различными свойствами объективно существуют конкретные связи. Они обусловливают соотношение между размерами физических величин, которые можно выразить в виде формулы. Поэтому если правильно выбрать единицы некоторых физических величин, то че­рез эти единицы можно выразить через единицы всех остальных физических величин.

Физические величины, размеры единиц которых выбирают произвольно, называют основными. Единицы измере­ния основных физических величин также называют основными. Единицы измерения всех остальных физических ве­личин выражают через основные и называют производными. Совокупность основных и производных единиц состав­ляет систему единиц измерения.

Системой СИ (система интернациональная) установлены физические величины, указанные в табл.1.

Для установления производных единиц измерения пригодны только формулы в виде степенных комплексов с постоянным коэффициентом, равным единице. Степенной комплекс, выбранный для установления производной еди­ницы измерения, называется определяющим уравнением для этой единицы, и выбирается так, чтобы оно содержа­ло не более четырех физических величин.

Формула размерности любой физической величины однозначно определяется выбором основных единиц измере­ния и определяющего уравнения. Однако одна и та же формула размерности может соответствовать различным физическим величинам. Например, в СИ размерность работы, энергии, момента силы, количества теплоты совпа­дают и равны L²Mt^-2.

Уравнение в виде степенного комплекса, не являющееся определяющим для единицы физической величины, мо­жет содержать в общем случае постоянный коэффициент k - 1, который может быть как безразмерной, так и размерной величиной.

Таблица 1 Основные единицы измерения

Величина	Единица измерения
Наименование	Символ	Наименование	Обозначение
международное	русское
Длина Масса Время Сила электрического тока Термодинамическая температура Количество вещества Сила света	L M t I Q N J	Метр Килограмм Секунда Ампер Кельвин Моль Кандела	m kg s A K mol cd	м кг с А К моль кд

Число размерных коэффициентов (физических констант) в формулах зависит от числа основных единиц изме-

рения. Чем больше это число, тем больше различных "универсальных" констант в физических формулах. Это

затрудняет запоминание формул, удлиняет вычисления, усложняет установление эталонов основных единиц. Чем

меньше число физических констант, тем проще физические формулы, но тем больше число единиц, обладающих

одинаковыми размерностями.

Аналоговое моделирование. Аналогия - это сходство различных объектов по некоторым признакам. Объекты, сходные по соответствующим признакам, называют аналогами, а признаки, по которым объекты оказываются ана­логами, сходственными.

Сходство аналогичных явлений состоит в одинаковом характере протекания процессов. Математически анало­гичные явления описываются формально одинаковыми уравнениями и условиями однозначности. Однако физическое содержание и размерность входящих в них величин различны. Основное значение состоит в возможности перено­са сведений с одного объекта на другой (аналог).

Аналогия широко используется для придания наглядности сложным явлениям при их изучении. Хорошо извест­на положительная роль аналогии электрического тока с движением жидкости при изучении прохождения тока в электрической цепи. Не менее широко она используется при формировании понятий и для иллюстраций. Примера­ми понятий, введенных по аналогии, являются теплоемкость, запоминающее устройство, электродвижущая сила. Примером, иллюстрирующим по аналогии понятие устойчивости, служит шарик на вогнутой поверхности в поле тяготения.

Наконец, аналогия позволяет перейти к важнейшему понятию подобия, обеспечивающему строгий пересчет данных модели в данные оригинала. Имеется в виду важнейший вид количественной аналогии - аналогия матема­тическая, т.е. сходство объектов по их математическому описанию. Наиболее полная математическая аналогия имеет место, если объекты описываются сходными функциями и уравнениями.

Аналогичное моделирование - это замещение оригинала аналогичной моделью, обладающей сходством с ориги­налом, достаточным для экстраполяции ее свойств и отношений в свойства и отношения оригинала на основании умозаключения по аналогии. Оно используется обычно при сравнительно слабой изученности оригинала, когда имеющиеся сведения об его свойствах носят только качественный характер.

В качестве примера можно рассмотреть электротепловую аналогию. В этом случае изучаемое явление - ста­ционарное температурное поле, а его аналогия - стационарное поле электрического потенциала.

Уравнение теплопроводности и уравнение электрического потенциала

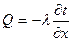
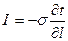
аналогичны. В безразмерной форме они будут тождественны.

Если созданы граничные условия для потенциала, аналогичные условиям для температуры, то в безразмерной форме они также будут тождественны (граничные условия первого и второго рода).

Исследование процессов теплопроводности методом аналогий

К числу экспериментальных методов исследования процессов теплопроводности относится метод аналогий.

В методе аналогий исследование тепловых явлений заменяется изучением аналогичных явлений (электричество, гидравлика).

Сходство аналогичных явлений состоит в одинаковом характере протекания этих процессов. Математические аномальные явления описываются формально одинаковыми дифференциальными уравнениями и условиями однозначности. Однако, физическое содержание и размерность входящих в них величин различны.

Остановимся более подробно на основных принципах и методах моделирования.

Электротепловая аналогия.

Явления теплопроводности и электропроводности подчиняются уравнением:

.

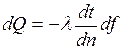
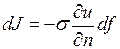где u – электрический потенциал;

s - коэффициент электропроводности.

Применение указанных уравнений к случаю двухмерной задачи при стационарных условиях протекания процессов во времени и при независимости физических свойств от температуры приводит к следующим дифференциальным уравнениям Лапласа:

.

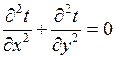
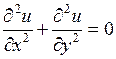То есть уравнения для температуры и электрического потенциала имеют одинаковую структуру. Аналогичные явления должны протекать и в геометрически подобных системах.

Граничные условия могут быть заданы различными способами. Допустим, что они задаются в виде следующих уравнений:

,

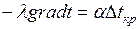
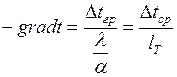где ,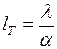

.

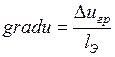Для установления количественной связи между аналогичными физическими величинами математические описания нужно проводить к безразмерному виду. Для этого в качестве масштаба для температурного напора можно принять некоторую величину 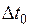, для электрического потенциала 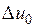, для линейных размеров сходственные линейные отрезки 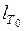и .

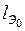Обозначив значения величины, выраженных в относительном масштабе, через большие буквы:

; ; .

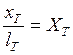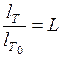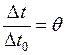Аналогичные соотношения имеют место для величин, относящихся к электрическому явлению.

После проведения к безразмерному виду уравнения, описывающие граничные условия принимают вид:

,

.

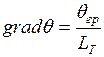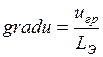Эти уравнения тождественно одинаковы, а следовательно и решения безразмерных уравнений теплопроводности и электропроводности одинаковы.

Рассмотрим примеры:

При разработке электрических моделей, имитирующих процессы теплопроводности, применяются два способа.

В одном способе электрические модели повторяют геометрию оригинальной тепловой системы и приготавливаются из материала с непрерывной проводимостью (электролит или электропроводящее тело). Модели такого типа называются моделями с непрерывными параметрами процесса. В них тепловые системы заменяются моделирующими электрическими цепями.

Согласно аналогии, напряжение в любой точке электрической модели соответствует температуре в той же точке тепловой системы.

В настоящее время электрическое моделирование получило большое развитие. Появился ряд установок, предназначенных для решения различных физических задач.

Гидротепловая аналогия

Гидротепловая аналогия может быть также использована для исследования как стационарных, так и нестационарных процессов теплопроводности.

В этом случае используется сходство законов распространения тепла и движения жидкости. В качестве моделей могут быть использованы, как модели с непрерывными параметрами, так и модели с сосредоточенными параметрами, т.е. в виде моделирующих гидравлических цепей. В последнем случае вместо параметров исходного теплового процесса в моделирующей цепи применяются сосредоточенные параметры в виде гидравлических сопротивлений и емкостей. При построении гидравлической модели используют обычно формальное сходство уравнения для плотности теплового потока.

.

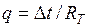С уравнением, выражающим расход жидкости при ламинарном движении.

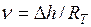
где 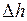- гидравлический напор;

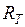- гидравлическое сопротивление.

Поскольку сопоставляемые явления изменяются во времени, то следует учесть изменение теплового потока и расхода жидкости во времени. Они выражаются:

,

.

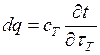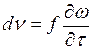где 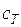- теплоемкость системы;

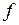- площадь поперечного сечения гидравлического канала;

w - скорость движения жидкости.

Из сравнения уравнений следует, что аналогом q является расход жидкости n, аналогом температурного напора является гидравлический напор Dh, аналогом теплоемкости - гидравлическая емкость, аналогом термического сопротивления – сопротивление 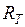в гидравлической модели.

Условие теплообмена на поверхностях стенки воспроизводится с помощью дополнительных сосудов. Уровень жидкости в них соответствует температурам. Тепловые сопротивления имитируют гидравлическими сопротивлениями капилляров. Уровень жидкости в сосудах воспроизводит начальное сопротивление температуры. Можно сделать фотосъемки уровней воды, замерить расход, после …. всех кранов и величин уровней будет характеризовать температуры. Если масштабы … гидравлической модели и теплового явления различны, то переход от модели к процессу производится через масштабные преобразования.

Физическое моделирование –это моделирование на физической модели процесса. Физическое моделирование базируется на подобных физических явлениях.

Основы теории подобия

Теория подобия – это учение о подобии явлений. Впервые с понятием подобия мы встречаемся в геометрии, откуда этот термин и был заимствован. Как, известно, геометрически подобные фигуры, например, треугольник обладает тем свойством, что их соответственные углы равны, а сходственные стороны пропорциональны:

,

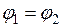
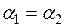
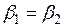
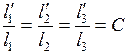Где С₁ – коэффициент пропорциональности, константа подобия.

Записанные нами выражения являются математической формулировкой геометрического подобия.

Понятие подобия может быть распространено на любые физические явления. Можно говорить, например, о подобии картины движения двух потоков жидкости, кинематическом подобии, о подобии сил, вызывающих подобие между собой движение динамическим подобии: о подобии картины распределения температур и тепловых потоков – тепловом подобии и т.д.

В общем случае понятие подобия физических явлений сводится к следующим положениям:

а) понятие подобия в отношении физических явлений применимо только к явлениям одно и того же рода, которые качественно одинаковы и аналитически описываются уравнениями одинаковыми по форме и содержанию.

Если же математическое описание двух каких-либо явлений одинаково по форме, но различно по физическому содержанию, то такие явления называют аналогичными. Такая аналогия существует между процессами теплопроводности, электропроводности, диффузии.

б) обязательной предпосылкой подобия физических явлений должно быть геометрическое подобие. Подобие означает, что подобные явления всегда протекают в геометрически подобных системах.

в) при анализе подобных явлений сопоставлять между собой можно только однородные величины и лишь в сходственных точках пространства и в сходственные моменты времени.

Однородными называются такие величины, которые имеют один и тот же физический смысл и одинаковую размерность. Сходственными точками геометрически подобных систем называются такие, координаты которых удовлетворяют условию:

; ; ;

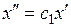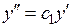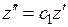Два промежутка времен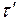и и 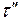называются сходственными, если они имеют общее начало отсчета и связаны преобразованием подобия:

.

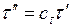Г) подобие двух физических явлений означает подобие двух величин, характеризующих рассматриваемые явления. Это значит, что в сходственных точках пространства и в сходственные моменты времени любая величина 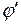- первого явления пропорционально однородной с ней величине 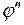второго явления:

.

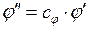Коэффициент 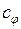константа подобия, ни от координат, ни от времени не зависит. При этом каждая функция величины 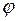имеет свою с.

Чтобы их различить обычно внизу справа ставят индекс той величины, к которой она относится 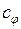, 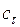и т.д.

Таким образом, сущность подобия двух явлений означает подобие полей одноименных физических величин, определяющих это явление.

Постоянные подобия для различных величин в подобных явлениях нельзя назначать или выбирать произвольно. Между ними всегда имеются строго определенные соотношения, которые выводят из математического описания процессов. Эти соотношения имеют центральное значение в теории подобия, так как они устанавливают существование особых величин, называемых числами подобия, которые во всех подобных явлениях сохраняют всякие определенные значения.

Числа подобия являются безразмерными комплексами, составленными из величин, характеризующих явления. Числа подобия принято называть именами ученых, работающих в соответствующей области науки, и обозначать двумя начальными буквами их фамилий Re, Nu и т.д.

Числа подобия можно получить для любого физического процесса. Для этого необходимо иметь его математическое описание. Последнее является необходимой предпосылкой теории подобия.

Без этого все учение о подобии свелось бы лишь к простому определению подобия.

Основные положения теории подобия можно сформулировать в виде трех теорем, к рассмотрению которых мы и приступаем.

Теорема первая устанавливает связь между постоянными подобия и позволяет выявить числа подобия. В общем виде она формулируется следующим образом: подобные между собой процессы имеют одинаковые числа подобия.

Теорема вторая. На основании второй теоремы подобия зависимость между переменными, характеризующими какой-либо процесс, может быть представлена в виде зависимости между числами подобия :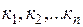

.

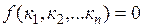Эту зависимость называют уравнением подобия, так как во всех подобных между собой процессов числа подобия сохраняют одно и то же значение, то уравнения подобия для них так же одинаковы. Следовательно, представляя результаты какого-либо опыта в числе подобия, мы получим обобщенную зависимость, которая справедлива для всех подобных между собой процессов.

До сих пор рассматривались свойства подобных между собой явлений, когда подобие уже существует. Однако возможна обратная постановка задачи: наши условия необходимы и достаточны, чтобы процессы были подобными. На этот вопрос дает ответ третья теорема подобия.

Подобны те процессы, условие однозначности которых подобны, и числа подобия, составлены из величин, входящих в условия однозначности, должны иметь одинаковые численные значения.

Из этой теоремы видно, что необходимо особо выделить числа подобия. Инвариантность определяющих чисел подобия является условием, которое должно быть выполнено для получения подобия.

Итак, теорема подобия позволяет не интегрируя дифференциальных уравнений, получить из чисел подобия, и используя опытные данные установить уравнение подобия, которые справедливы для всех подобных между собой процессов. Однако, все эти выводы конечно ограничены условиями подобия и делать выводы нельзя, выходить за их пределы.

Условия подобия конвективного теплообмена при вынужденном движении

На практике встречается большое число разнообразных задач, в которых теплообмен происходит в условиях вынужденного движения теплоносителя. Они различаются по геометрической форме и конфигурации систем, в которых протекает процесс теплообмена по кинематической картине и режиму течения потока. Различными могут быть также и сами теплоносители – жидкости и газы.

Прежде всего, подобными могут быть лишь процессы теплообмена, протекающие в геометрически подобных системах. Далее необходимой предпосылкой подобия должно быть подобие полей скорости, температур и давлений во входном или начальном сечении таких систем. При выполнении таких условий стационарные процессы конвективного теплообмена при вынужденном движении будут подобны, если выполняются условия:

,

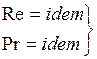где 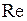- число Рейнольдса, мы с ним уже встречались и определяется как ,

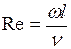где 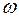- скорость движения жидкости;

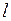- характерный размер (длина пластины, диаметр и т.д.);

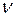- кинематическая вязкость.

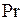- число Прандтля. Оно является теплофизической характеристикой самого теплоносителя. Оно составлено лишь из физических параметров:

.

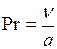При равенстве чисел 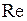, условие одинаковости чисел 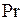обеспечивает тепловое подобие, т.е. подобие полей температурных напоров и тепловых потоков во всем объеме рассматриваемых систем.

Согласно теории подобия у подобных процессов должны быть одинаковы также и определяемые числа подобия. В процесса конвективного теплообмена в качестве определяемого выступает число Нуссельта - 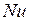, характеризующее интенсивность процесса конвективного теплообмена:

,

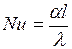где 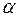- коэффициент теплопередачи;

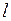- характерный геометрический размер;

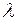- коэффициент теплопроводности теплоносителя.

Итак, условие 1 представляет собой условие интенсивности определяющих чисел подобия. Этим обеспечивается подобие процессов. Инвариантность определенного числа подобия (числа 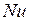) является уже следствием установившегося подобия.

Уравнение подобия для процессов конвективного обмена при вынужденном движении теплоносителя имеет вид:

.

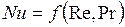Условие подобия процессов теплообмена при свободной конвекции

Процесс свободной конвекции возникает из-за различия плотностей нагретых и холодных частиц теплоносителя. Для большинства теплоносителей в том интервале температур, который обычно встречается на практике, зависимость плотности от температуры с достаточным приближением может рассматриваться как линейная. Так если в дали от нагретого тела температура теплоносителя составляет 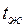, а в некоторой точке около поверхности равна 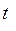, то соответствующее значение плотност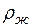и и 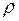связаны уравнением:

,

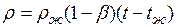где 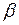- температурный коэффициент объемного расширения среды.

Так как 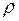< 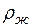, то на частицы нагретой жидкости, имеющей температуру 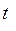, действует подъемная архимедова сила, равная:

.

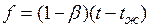
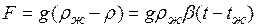Эта сила и вызывает конвективное движение среды. Из этого уравнения видно, что подъемная сила будет тем больше, чем выше значения следующих величин 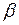и .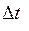

Процессы свободной конвекции широко распространены в различных областях современной техники. Однако, несмотря на разнообразие практических схем их осуществление, для всех таких процессов условие падения имеют универсальный вид, определяемый теорией подобия.

1. Прежде всего подобными могут быть процессы, протекающие в геометрически подобных системах.

2. Далее – подобие температурных полей на поверхностях нагрева или охлаждения. При выполнении этих требований стационарные процессы свободной конвекции будут подобны, если выполняются условия:

.

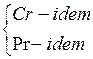Число 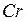- характеризует относительную эффективность подъемной силы, вызывающий свободно конвективное движение среды, оно имеет вид:

,

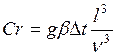где 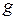- ускорение свободного падения;

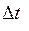- перепад температур или температурный напор;

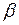- температурный коэффициент объемного расширения;

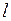- характерный линейный размер системы;

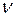- кинематический коэффициент вязкости.

Число 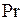является теплофизической характеристикой теплоносителя:

,

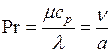Выполнение выше записанных условий обеспечивает подобие процессов свободной конвекции, т.е. подобие полей температурных напоров тепловых потоков и скоростей в геометрически подобных системах. При выполнении этих условий определяемое число подобия – число Нуссельта. 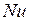также оказывается одним и тем же в таких системах:

.

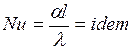Математическое моделирование - это замещение оригинала математической моделью, обеспечивающей фиксацию и исследование свойств и отношений оригинала, а также переход к оригиналу с помощью математических мето­дов.

Сходство объектов по их математическому описанию, т.е. математическая аналогия, при определенных усло­виях превращается в математическое подобие или просто подобие.

Методы оптимизации

Решение оптимизационных задач составляет важную, если не основную, часть работы инженера. Термин "оптимум происходит от латинского слова "optimum", что означает наилучшее и означает совокупность наибо­лее благоприятных условий протекания какого-либо процесса. Таким образом, оптимизация-это процесс перевода изучаемого процесса или явления в состояние, отвечающее оптимуму целевой функции. Широкое использование методов оптимизации в промышленности и науке обуславливается двумя причинами: Во-первых традиционный детерминистский подход, когда ученые пытались строить модели реальных технологических процессов на основе небольшого числа физических законов, оказался неконструктивным с точки зрения управления процессом и в значительной мере исчерпал свои возможности;

во-вторых, возникшая в 40 годах кибернетика предложила заменить традиционное изучение механизма яв­ления концепцией черного ящика, при которой на первый план выдвигается решение задачи управления процес­сом или объектом на основе его математической модели

Постановка и решение оптимизационных задач включает в себя решение ряда последовательных задач. Прежде всего надо определиться надо или нет оптимизировать, что оптимизировать и как оптимизировать. В настоящее время существует большое количество методов поиска оптимумов, которые можно разделить на три основные группы в зависимости от уровня информированности исследователя об исследуемом процессе. Не­посредственно перед началом исследования исследователь может находиться на одном из трех уровней информи­рованности: детерминированном, стохастическом и неопределенном.

Детерминированным называется такой уровень информированности, при котором точно известна математи­ческая модель процесса, при стохастическом уровне известны априорные функции распределения параметров ма­тематической модели процесса, при неопределенном-известны только вероятные границы управляемых процессов, но не известны функции распределения параметров и другие вероятностные характеристики процесса. Уровень информированности определяет подход к проблеме оптимизации, на детерминированном уровне определяется ис­тинный оптимум процесса, на стохастическом уровне определяется оптимум процесса, отвечающий максимальному математическому ожиданию критерия оптимизации, на неопределенном уровне оптимум определяется на основе теоретико-игрового подхода. Приведенная классификация методов оптимизации не является единственной, мето­ды оптимизации исторически развивались независимо друг от друга на основе различных концепций, идей, подходов и поэтому можно предположить и другие схемы классификации. Не существует резкой грани между тре­мя различными подходами к проблеме оптимума. В зависимости от требуемой точности определения оптимума и соотношения между выигрышем от оптимизации процесса и затратами на получение информации о процессе расс­матриваемый процесс может быть изучен с большей или меньшей достоверностью и оптимизация его может прово­диться на любом из названных уровней. По используемому математическому аппарату методы оптимизации можно разделить на следующие: вариационное исчисление, принцип максимума Понтрягина, динамическое программиро­вание, градиентные методы оптимизации, методы случайного поиска, линейное, нелинейное и целочисленное программирование.

Сиплексный метод оптимизации

Симплексный метод оптимизации, предложенный В Спиндлеем и др. в 1962 году характеризуется простотой и высокой эффективностью и нашел свое применение в различных отраслях науки и техники. Он не требует вы­числения производных, эффективен для обнаружения условных и безусловных экстремумов и особенно эффективен при большом количестве переменных. В центре метода находится понятие симплекса. Симплексом называется простейшая выпуклая геометрическая фигура, образованная множеством ( к+1) называемых точек в к-мерном пространстве и обладающая минимальным количеством вершин. Вершинами называются точки, образующие симп­лекс. В пространстве нулевой размерности симплекс представляет собой точку, в пространстве размерности 1, представляющем собой прямую-отрезок, в двумерном пространстве-треугольник, в трехмерном пространстве- пи­рамиду. Сиплекс называется регулярным, если расстояния между его вершинами равны, в двумерном пространс­тве-это равносторонний треугольник, в трехмерном пространстве- тетраэдр, в четырехмерном пространстве-ги­пертетраэдр. При оптимизации используется основное свойство симплекса-из любого симплексаможно, отбросив одну из вершин и используя оставшуюся грань, получить новый симплекс, добавив всего одну точку. Поиск оп­тимума симплекс-методом осуществляется последовательным перемещением симплексов с помощью зеркального от­ражения вершин, имеющих наихудшее значение параметра оптимизации.

В настоящее время существует несколько модификаций метода, рассмотрим основной из них, который в на­ибольшей степени подходит для экспериментальной оптимизации, если необходимо найти значения переменных х х х х, при которых достигается максимум критерия y.

1. Выбирается исходная точка в пространстве заданных переменных, которая принимается за центр симп­лекса. Выбор исходной точки сводится к определению значений переменных х₁ х₂ х_n , которые представляют собой исходную точку в заданном к-мерном пространстве. Выбор такой точки не поддается никаким формальным прави­лам и производится исследователем на основе имеющейся в его распоряжении информации, его опыта и интуи­ции. исходная точка должна быть как можно ближе к оптимуму, и если она представляет собой оптимум, то дальнейшие операции теряют смысл, что, впрочем, может быть чисто случайно и поэтому наблюдается весьма редко, а в общем сучае исходная точка находится на каком-то расстоянии от оптимума и величина этого расс­тояния неизвестна.

2. Выбирается величина интервала варьирования по каждому фактору х₁ х₂.. х_n . При выборе интервала варьирования факторов необходимо учитывать, что уменьшение интервалов варьирования увеличивает точность определения оптимума, но требует большего количества экспериментов или вычислений, а увеличение интерва­лов действует в противоположном направлении, поэтому необходимо выбирать эти величины исходя из компро­мисса между этими двумя требованиями.

3. По таблицам координат вершин симплекса, которую можно рассматривать, как план эксперимента в ко­дированных переменных аналогично тому, как это делается в методологии планируемого эксперимента, определя­ется их значения.

4. Осуществляется отражение худшей вершины симплекса, то есть отражается вершина, где значение параметра y наименьшее среди всех вершин симплекса в случае, если задача состоит в определении точки, где значение параметра y достигает максимума или отражается вершина с максимальным значением y, если задача состоит в определении точки в факторном пространстве, где параметр y достигает минимума.

5. Окончание процесса поиска оптимума симплекс методом может быть сформулировано на основе следующих соображений. Во-первых, движение симплекса не имеет смысла продолжать, если длительное перемещение симплекса не приводит к улучшению параметра y, чаще всего это происходит при вращении симплекса вокруг лучшей точки. Такое явление вращения симплекса называется зацикливанием. Во-вторых, если разница в значениях параметра оптимиза­ции худшей и лучшей из вершин симплекса находится в пределах погрешности измерения параметра y, то также процесс поиска оптимума заканчивается.

Преимущества метода: метод очень прост и подходит как для аналитической так и для экспериментальной оптимизации. - экономичность, ввиду того, что количество экспериментов ( циклов) равно к+1

Недостатки метода. - недостаточная точность определения положения оптимума.

Метод Гауса - Зейделя

Метод Гауса-Зейделя, или метод поочередного изменения координат является простейшим методом оптими­зации и широко применяется в инженерной практике. при оптимизации этим методом осуществляется последова­тельное продвижение осуществляется с помощью поочередного варьирования каждым параметром до достижения частного экстремума параметра оптимизации. алгоритм следующий:

1-выбирается исходная точка и шаг варьирования и начинается варьирование в направлении оси х

2- производится сравнение полученных значений параметра у₁ у₂ и при поиске максимума выбирается нап­равление возрастания параметра у ( при поиске минимума- направление убывания)