Механические характеристики пластичности и твердости материалов
По диаграммам испытаний металлических образцов на растяжение определяются также такие характеристики пластичности материала, как
а) относительное удлинение 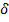 ;
;
б) относительное поперечное сужение  .
.
Относительное удлинение рассчитывается по формуле:

где 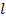 – первоначальная (расчетная) длина образца;
– первоначальная (расчетная) длина образца;
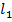 – длина образца после разрушения (разрыва).
– длина образца после разрушения (разрыва).
Таким образом, относительное удлинение, как механическая характеристика пластичности материала, есть измеренное в процентах отношения изменения длины образца после разрушения к его первоначальной длине.
Относительно поперечное сужение определяется зависимостью;

где  – первоначальная площадь поперечного сечения образца;
– первоначальная площадь поперечного сечения образца;
 – площадь поперечного сечения шейки образца после разрушения.
– площадь поперечного сечения шейки образца после разрушения.
Следовательно, относительное поперечное сужение характеризуется изменением в процентах отношения площади сечения образца после разрушения к его первоначальной площади до проведения испытаний.
Чем больше значение величин 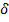 и ψ, тем пластичнее материал, т.е. он может лучше принимать пластическую деформацию. Такие материалы предпочтительно использовать на практике, они лучше воспринимают ударное действие нагрузок и низкие температуры.
и ψ, тем пластичнее материал, т.е. он может лучше принимать пластическую деформацию. Такие материалы предпочтительно использовать на практике, они лучше воспринимают ударное действие нагрузок и низкие температуры.
К механическим характеристикам пластичности относиться также угол загиба стального образца. Это механическая характеристика определяет такой допустимый угол загиба образца  , при котором не должно быть трещин в растянутой зоне образца (рис.7.6).
, при котором не должно быть трещин в растянутой зоне образца (рис.7.6).

Рисунок 7.6 – Испытания на угол загиба образца
Еще одной характеристикой пластичности материала является ударная вязкость  , которая рассчитывается по формуле:
, которая рассчитывается по формуле:

где  – работа на разрушение образца в месте надреза;
– работа на разрушение образца в месте надреза;  – площадь сечения образца в ослабленном надрезом месте (рисунок 7.7).
– площадь сечения образца в ослабленном надрезом месте (рисунок 7.7).

Рисунок 7.7 – Виды образцов по определению ударной вязкости материала
Испытания образцов стандартны размеров производят на специальном оборудовании (маятниковый копр) путем их ударного разрушения и определения работы на разрушения образцов А.
Ударная вязкость характеризует так же свариваемость стали.
Твердость, как механическая характеристика состояния поверхности материала, определяется вдавливаниемв образец стального шарика или алмазных призмы, конуса (испытания называются по именам их авторов Бринеля, Виккерса, Роквела). Так, твердость материала в единицах по Бринелю рассчитывается по формуле:

 где
где  – усилие по вдавливанию шарика в материал;
– усилие по вдавливанию шарика в материал; 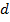 – диаметр шарика;
– диаметр шарика;  – глубина вдавливания шарика в материал.
– глубина вдавливания шарика в материал.
Рисунок 7.8 – Испытания твердости материала по Бринелю
Часть 2. ИЗГИБ, УСТОЙЧИВОСТЬ БАЛОК И ДОПОЛНИТЕЛЬНЫЕ ВОПРОСЫ СОПРОТИВЛЕНИЯ МАТЕРИАЛОВ
· изгиб балок
· устойчивость балок
· прочность при динамических нагрузках
· концентрация напряжений
· усталостная прочность
· краткие сведения о ползучести и релаксации
· основные понятия о пластическом деформировании балок
Изгиб балок
Общие положения об изгибе. Опоры и опорные реакции
Одним из наиболее распространенных элементом судостроительных, машиностроительных и других конструкций являются балки. Напомним, что балкой называется стержень с прямолинейной осью, работающий в основном на изгиб. Изгибом же называют такой вид деформации балки, которая искривляется (изгибается) под действием внешних нагрузок (сосредоточенных и распределенных сил, внешних активных моментов). Осью балки называется геометрическое место центров тяжести сечений до ее нагружения (рис. 8.1, а). А при действии внешних нагрузок ось балки искривляется и превращается в упругую линию балки.

Рисунок 8.1 – Ось и упругая линия балки
Деформация балки характеризуется двумя величинами: 1) прогибом (перемещением)  точки А балки перпендикулярно к ее оси; 2) углом поворота
точки А балки перпендикулярно к ее оси; 2) углом поворота  поперечного сечения в результате изгиба балки по отношению к ее первоначальному положению (рис. 8.2). Расчетная схема балки, работающей на изгиб, показывается линиями: прямой – до деформации; кривой (пунктиром) – после деформации. Заметим, что при малых деформациях балок перекрытий (
поперечного сечения в результате изгиба балки по отношению к ее первоначальному положению (рис. 8.2). Расчетная схема балки, работающей на изгиб, показывается линиями: прямой – до деформации; кривой (пунктиром) – после деформации. Заметим, что при малых деформациях балок перекрытий (  ) углы поворота сечений
) углы поворота сечений  приблизительно равны углам наклона к горизонтальной линии (оси) касательной упругой линии
приблизительно равны углам наклона к горизонтальной линии (оси) касательной упругой линии 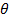 (см. рис. 8.2).
(см. рис. 8.2).

Рисунок 8.2 – Расчетная схема балки при изгибе и ее деформации
В расчетах изгиба балок начало системы координат обычно принимается на левом конце балки (т.О), продольная ось х имеет положительное направление вправо от начала координат, а положительное направление вертикальной оси у – вверх (см. рис. 8.2).
В сопротивлении материалов рассматриваются, в основном, балки с постоянным сечением по ее длине и называются призматическими. Балки с одним опорным закреплением (защемлением, заделкой) именуются консольными, а с двумя опорами по концам (см. рис. 8.2) – однопролетными.
Особенностью балок в составе конструкций является наличие опор (опорных закреплений) по концам Балки служат для передачи действующих нагрузок на опоры, которые их поддерживают.
В сопротивлении материалов рассматриваются такие простейшие типы опор, схематическое изображение которых показано на рисунке 8.3:
1) шарнирно-неподвижная опора;
2) шарнирно-подвижная опора;
3) неподвижная жесткая заделка (защемление);
4) подвижная жесткая заделка.
Шарнирно-неподвижная опора (рис.8.3, а) исключает вертикальное и горизонтальное перемещение опорного сечения(  ), но позволяет только поворот в шарнире вокруг нее на угол
), но позволяет только поворот в шарнире вокруг нее на угол 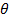 . В общем случае на этой опоре возникают вертикальная и горизонтальная реакции Rу и Rх.
. В общем случае на этой опоре возникают вертикальная и горизонтальная реакции Rу и Rх.

Рисунок 8.3 – Типы опор балок
Шарнирно-подвижная опора (рис. 8.3, б) препятствует вертикальному смещению балки в опорном сечении(𝓌  ), но имеют место горизонтальное смещение опоры
), но имеют место горизонтальное смещение опоры  и угол поворота опорного сечения
и угол поворота опорного сечения 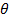 . На этой опоре возникает только вертикальная реакция R=Rу, а горизонтальная реакция отсутствует (Rх = 0).
. На этой опоре возникает только вертикальная реакция R=Rу, а горизонтальная реакция отсутствует (Rх = 0).
Неподвижная жесткая заделка (защемления  рис. 8.3, в) накладывает на балку условия отсутствия не только горизонтального и вертикального смещения (
рис. 8.3, в) накладывает на балку условия отсутствия не только горизонтального и вертикального смещения (  ), но и поворота опорного сечения (
), но и поворота опорного сечения (  ). В опоре в общем случае возникают вертикальная и горизонтальная реакции Rу ,Rх и реактивный момент М3.
). В опоре в общем случае возникают вертикальная и горизонтальная реакции Rу ,Rх и реактивный момент М3.
Подвижная жесткая заделка (рис. 8.3, г) позволяет перемещение опорного сечения только в горизонтальном направлении u при отсутствии вертикального перемещения и угла поворота сечения на опоре (  ). В ней возникают только вертикальная реакция Rу и реактивный момент М3.
). В ней возникают только вертикальная реакция Rу и реактивный момент М3.
В заключение общих положений подраздела отметим виды изгиба при действии на балку внешних нагрузок, лежащих в одной из главных плоскостей инерции поперечного сечения. Так, при расположении силовых факторов в координатной плоскости хОу рассматривают такие виды изгиба:
а) чистый изгиб, который производится двумя внешними (активными) моментами 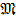 , направленных в противоположные стороны (рис. 8.4, а);
, направленных в противоположные стороны (рис. 8.4, а);
б) плоский поперечный изгиб, когда в пролете балки может быть нагрузка, не перпендикулярная к ее оси (рис.8.4, б);
в) прямой поперечный изгиб (именуемый зачастую как поперечный изгиб) при действии перпендикулярных к оси балок нагрузок (рис. 8.4, в).

Рисунок 8.4 – Виды изгиба балок
