Определение плотности твердого тела правильной формы

Цель работы:

1. Определение плотности твердого тела путем взвешивания на рычажных весах.

2. Овладение методикой работы с микрометром, штангенциркулей и техническими весами.

3. Приобретение навыков обработки экспериментальных результатов ори прямых в косвенных измерениях.

Приборы в принадлежности: I. Технические весы и разновес.

2.Микрометр.

3.Штангенциркуль.

4.Металлические цилиндры.

1.1Теоретическое введение

Масса - физическая величина, являющаяся мерой инерционных и гравитационных свойств материи, а также ее полной анергии.

Инерционностью называется свойство тел сохранять состояние покоя или прямолинейного и равномерного движения. Чем больше масса тела, тем меньшее ускорение оно приобретает под действием приложенной к нему силы.

В соответствии с законом всемирного тяготения, сила взаим­ного притяжения тел, находящихся на расстоянии прямо пропорцио­нальна величинам их масс и обратно пропорциональна квадрату рас­стояния между ними. В этом законе природы проявляются гравитаци­онные свойства массы.

И, наконец, аз закона взаимосвязи массы и энергии следует, что масса является мерой полной энергии тел и зависит от скорости их движения.

Таким образен, масса выступает как одна аз важнейших харак­теристик, необходимых для описания физических явлений.

Штангенциркуль состоит из масштабной линейки -штанги (рис. I) и рамы С, которая перемещается по линейке, масштабная линейка (или основная шкала) имеет выступ А. Такой же выступ В имеет и рама С. Измеряемое тело зажимается между этими выступами и может быть закреплено с помощью винта Н. На штангу наносится основная шкала; позволяющая сделать отсчет целых миллиметров, а на раму наносится дополнительная шкала - нониус, с помощью которой производится отсчет долей миллиметра. Нулевой штрих масштабной линейки расположен на некотором расстоянии от выступа А так, что при нулевом показании совпадает с нулем нониуса.

Масштаб шкалы нониуса выбирается так, чтобы(n — I)деле­ние основной шкалы соответствовали n - делениям нониуса. Например, на рис. I показано, что девять делений основной шкалы равны десяти делениям нониуса. Таким образом, одному делению нониуса соответствует часть (n – 1)/n от цены деления основной шкалы.

Микрометр (рис. 2) состоит из микрометрического винта С и рамки с неподвижным выступом А. С другой стороны к этой рамке присоединена неподвижная линейная шкала. При вращении мик­рометрического винта одновременно, вращается цилиндр В, закры­вающей линейную шкалу. На краю цилиндра нанесена круговая шка­ла.

Дня проведения измерений тело помещают между выступами и слегка зажимают, вращая головку винта до тех пор, пока она не будет издавать треск при попытке дальнейшего вращения.

На линейной шкале нанесены внизу миллиметры, вверху - по­ловины миллиметра. Один оборот винта соответствует перемещению цилиндра вдоль линейной шкалы на 0,5 мм. На круговой шкале имеется 50 делений, следовательно, каждому делению соответствует 0,01 мм. На линейной шкале берут целые миллиметры и их половины, а по круговой шкале отсчитываются сотые доли миллиметра.

Величина, численно равная массе, содержащейся в единице объема, называется плотностью однородного вещества

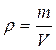, (1.1)

где ρ – плотность;

m –масса;

V - объем.

В настоящей работе проводится экспериментальной определение плотности металлических цилиндров правильной формы, изготовленных из различных сплавов. Масса определяется путем взвешивания на рычажных весах. Объем вычисляется по формуле

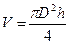(1.2)

где h ,В - высота и диаметр цилиндра соответственно.

С учетом (2) выражение (I) для плотности примет вид

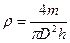(1.3)

Для определения диаметра и высоты используется микрометр и штангенциркуль.

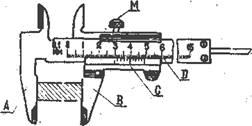
рис.1

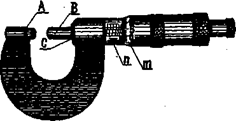
рис.2

1.2. Порядок выполнения работы

1.2.1. Измерьте не менее трех раз в различных местах вы­соту цилиндра штангенциркулем и диаметр - микрометром.

1.2.2. Взвесьте три раза тело, поочередно кладя его на правую и левую чашки весов.

Результаты всех измерений пунктов I и 2 занесите в табл. I

№ опыта	Высота h, мм	Диаметр D, мм	Масса m, г
измерен.	абс.ошиб.	измерен.	абс.ошиб.	измерен.	абс.ошиб.
Сред.

1.2.3.Определите среднее значение измеряемых величин и по формуле (3) вычислите плотность тела.

1.2.4.Определите относительную и абсолютную погрешности по формулам:

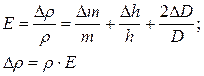(4)

1.2.5. Окончательный результат представьте в виде

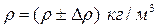
1.2.6. По значению величины плотности определите материал цилиндра.

3. Контрольные вопросы

1.3.1. Дайте определение массы, плотности, веса и удельного веса тела.

1.3.2. С какой точностью проводятся измерения штангенциркулем и микрометром?

1.3.3. Какие измерения называются прямыми и какие косвенными?

1.3.4. Дайте определения абсолютной и относительной погрешностям измерений. Как они вычисляются?

Литература

Савельев И. В. Курс общей физики, ч. I, гл.II М., 1977.

Кортнев А.В. , Рублев Ю.В. Куценко А.Н. Практикум по физике. М., 1975, стр. 15-34.

ЛАБОРАТОРНАЯ РАБОТА № 2

"ОПРЕДЕЛЕНИЕ УСКОРЕНИЯ СИЛЫ ТЯЖЕСТИ ПО СПОСОБУ БЕССЕЛЯ"

Цель работы: Экспериментальное изучение гармонических колеба­ний с помощью математического маятника.

Определение ускорения силы тяжести по способу Бесселя.

Приборы и принадлежности:

1. Математический маятник.

2. Секундомер.

2.1. Теоретическое введение

Колебаниями называется процессы, характеризующие повторяемость во времени. В механике примерами таких явлений могут служить колебания маятников, струн, мембран, камертонов, судна на волне и т.д. Если изменяющаяся в процессе, колебаний физическая величина х. Принимает определенные значения через равные промежутки времени, то такие колебания является периодическими.

Частным случаем периодических колебаний являются гармонические колебания, в которых изменение физической величины происходит по гармоническому закону, т.е. по закону синуса или косинуса:

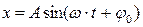
или

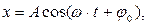
где х - смещение из положения равновесия;

А - амплитуда (максимальное смещение);

φ₀ - фаза колебаний;

ω∙t + φ_о - начальная фаза, соответствующая начальному моменту времени t = 0;

ω - циклическая или круговая частота.

Время, в течение которого совершается одно полное колеба­ние, называется периодом Т, а число колебаний за единицу времени (за одну секунду) - частотой колебаний

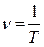
Поскольку период гармонических функций равен 2π , то циклическую частоту можно представить в виде:

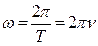
Таким образом, циклическая частота равна числу колебаний за 2π секунд.

Скорость υ и ускоренна Q при колебательном движении выражаются соответственно первой и второй производной от сме­шения х по времени t. Если смещение задано в виде:

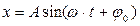, (2.1)

то

С учетом формулы (2.1) последнее уравнение можно записать:

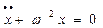(2.4)

которое представляет собой дифференциальное уравнение гармони­ческого осциллятора. Гармоническим осциллятором принято назы­вать любую систему, колебательный процесс которой описывается уравнением (2.4). Не трудно видеть, что уравнение (2.1) явля­ется решением дифференциального уравнения гармонического осцил­лятора.

В качестве примера рассмотрим гармонические колебания ма­тематического маятника.

Математическим маятником называется материальная точка, ко­лебавшаяся на невесомой и нерастяжимой нити.

Чтобы найти уравнение движения маятника рассмотрим динами­ку колебательного процесса. Силу тяжести, действующую на материаль­ную точку можно разложить на две составляющие: одна из которых Pn направлена вдоль нити и уравновешивается силой натяжения Fn;

вторая - Р_τ - перпендикулярна к нити и направлена по касательной к траектории движения.

Составляющая Р_τ является квазиупругой силой, под действием которой совершаются колебания.

Если нить отклонена от положения равновесия на угол α.

Р_τ = - Р∙sin α = - m∙g∙sin α (2.5)

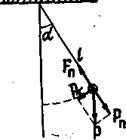
рис.1

Знак "-" указывает на то, что направление действия силы противопо­ложно направлению увеличения угла а. Рассматривая малые углы, для которых sina ≈ a, будем иметь:

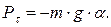(2.6)

Умножим уравнение (2.6) на длину нити l:

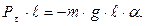(2.7)

В правой части выражения (7) мы имеем момент силы Р_τ , который можно в соответствии о основным законом динамики враща­тельного движения выразить через момент инерции

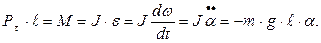(2.8)

Подставляя значение момента инерции материальной точки и проводя элементарные преобразования, получим:

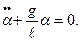(2.9)

Таким образом, процесс колебания математического маятника для малых углов описывается дифференциальным уравнением гармонического осциллятора.

В результате сравнения формул (2.9) в (2.4) находим, что

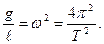
Период колебаний маятника равен

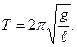(2.10)

Измеряя период колебаний Т и расстояние lот точки подвеса до центра тяжести тела с сосредоточенной массой, по формуле (2.10) можно определять величину ускорения силы тяжести. Однако измерение длины нити lне всегда является удобным, из-за трудностей определения положения центра тяжести тела, особенно, если оно не является сферически симметричным. Этих трудностей можно избежать, если воспользоваться способом Бесселя. Для этого нужно знать периоды колебаний и разность длин двух математических маятников.

Действительно, из формулы (2.10) квадраты периодов колеба­ний математических маятников с длинами l₁и l₂соответствен­но равны

;

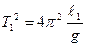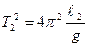
Вычитая из первого уравнения второе и разрешая относитель­но g, получим

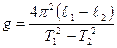(2.11)

В эксперименте с помощью специального устройства изменяют длину нити математического маятника, а по вертикальной неподвижно закрепленной линейке измеряют лишь разность длин l₁ – l₂ = h. Тогда ускорение силы тяжести можно вычислить по формуле

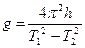(2.12)

2.2. Порядок выполнения работы

2.2.1. Взять возможно большую длину маятника и сделать отсчет по шкале (h₁)

2.2.2. Вывести маятник из положения равновесия так, чтобы угол отклонения составлял (4-6)° и, пропустив 2-3 колебания, опре­делить с помощью секундомера время 100 полных колебание.

Для данной длины маятника опыт повторить три раза я результат намерений занести в табл. I.

Таблица I

№ пп	Длинный маятник	Короткий маятник
Отчет по шкале h1, см	Абсолют. ошибка, Δh1, см	Время 100 колебаний, с	Период, Т1, с	Абсолют. ошибка, ΔТ1, с	Отчет по шкале h2, см	Абсолют. ошибка, Δh2, см	Время 100 колебаний, с	Период, Т2, с	Абсолют. ошибка, ΔТ2, с	Разность длин, h, см
Ср.

2.2.3. Укоротить длину нити маятника на 80-90 см, сделать отсчет по шкале (h₂) и повторить измерения пункта 2.

2.2.4. Определить средние значения величин Т₁,Т₂, h = h₁ – h₂ и, подставляя полученные значения в формулу (12) вычис­лить ускорение g_ср.

2.2.5. Определять относительную и абсолютную погрешности соответственно по формулам

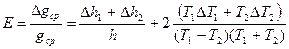(2.13)

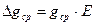(2.14)

2.2.6. Результаты измерений представить в виде

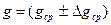
Контрольные вопросы

1. Какие колебания называется гармоническими? Напишите уравнение гармонических колебаний.

2. Дайте определение математического маятника.

3. Выведите формулу периода колебаний математического маятника. Почему этой формулой можно пользоваться в том случае, когда амплитуда колебаний мала?

4. Почему в данной работе для определения ускорения силы тяжести измеряют периоды и разность длин двух математических маятников.

5. Подучите формулы (2.13) и (2.14).

Литература

1. Детлаф А.А., Яворский Б.М., Милковская Л.Б. Курс физики, ч. I.М., 1973, стр. 152-156.

2. Савельев И.В. Курс общей физики, ч.I, М.,1977,гл.IX.

3. Кортнев А.В., Рублев Ю.В., Куценко А.Н. Практикум по физике, М., 1963.

ЛАБОРАТОРНАЯ РАБОТА № 3

ОПРЕДЕЛЕНИЕ УСКОРЕНИЯ СИЛЫ ТЯЖЕСТИ НАБЛЮДЕНИЕМ СВОБОДНОГО

ПАДЕНИЯ ТЕЛА

Цель работы: Определить ускорение силы тяжести при наблюдения свободного падения тела, измерить скорость падения тела и убедиться в справедливости закона сохранения энергии в механике.

Приборы и принадлежности:

1. Штатив с линейкой и отвесом.

2. Электронный секундомер Ф209.

3. Электромагнит с источником тока (4в),

4. Приставка "НЗ" (с нормально закрытыми контактами)
к секундомеру.

5. Стальной шарик.

6. Весы и разновес.

3.1. Теоретическое введение

Свободное падение тела есть движение под действием силы тяжести, и описывается следующими уравнениями:

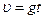(3.1)

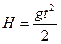(3.2)

Пользоваться этими уравнениями можно, если в условиях опыта ускорение силы тяжести постоянная величина. Проверим справедливость этого положения. Для этой цели запишем закон всемирного тяготения к случаю взаимодействия земного шара с телом, расположенным вблизи земной поверхности

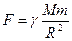(3.3)

где F - сила взаимного притяжения массы М Земли и массы m тела, находящегося у ее поверхности, расстояние между центрами тяготеющих масс А = 6400 мм, γ - гравитационная постоянная. С другой стороны, согласно второму закону динамики,

F = mg, (3.4)

из формул (3.3) и (3.4) следует, что 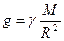(3.5).

Формула (3.5) показывает, что ускорение силы тяжести зависит от А. В условиях опыта А меняется в пределах I метра (ΔА ≈ 1 м), т.е. в пределах того расстояния, которое проходит тело при своем падении. Тогда относительная ошибка, которую мы сделаем, принимая A = const будет равна.

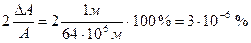
Эта ошибка по своей малости находится далеко за пределами самых точных измерений длин. Итак, в условиях опыта можно положить g = const и пользоваться кинематическими формулами (3.1) и (3.2).

Для определения g необходимо измерить время t падения тела о высоты Н. В настоящее время точно измерить эту величину можно с помощью электронного секундомера. При этом сопротивлением воздуха можно пренебречь, так как в условиях опыта наблюдается падение тяжелого маленького шарика с небольшой высоты. Для повыше­ния точности определения g рекомендуется измерить время падения о двух высот и рассчитать силы тяжести по формуле

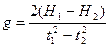(3.6)

Определив на опыте g, а также скорость падения по формуле (3.1), можно найти потенциальную энергию тела на высоте Н и его кинетическую энергию

П = mgH; (3.7)

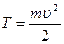(3.8)

При тщательном проведении опыта и многократном его повторении для каждой новой высоты Н, можно убедиться в справедливости закона сохранения энергии П + Т = Е = const.

3.2. Порядок выполнения работы

3.2.1.Взвесьте шарик на рычажных весах, данные внесите в табл. I.

3.2.2.Ознакомьтесь с описанием установки. Включите вилки миллисекундомера и электромагнита в сеть.

3.2.3.Нажмите кнопки миллисекундомера "сеть" и "I", "кон­такт", "вибрация". Тумблер "пуск" переведите в верхнее положение, кнопкой "сброс" установите миллисекундомер на ноль.

3.2.4.Укрепите электромагнит на штативе на некотором рассто­янии от планки, на которую падает шарик. Значение величины Н₁ внесите в табл. I.

3.2.5.Тумблер "магнит" поставьте в положение "вкл", а нижнюю планку установите в горизонтальное положение.

3.2.6.Прикрепите шарик к магниту и переведите тумблер "магнит" в положение "выкл".

3.2.7.Снимите показание времени падения шарика и результат занесите в табл. 2. Проделайте опыт не менее пяти раз.

3.2.8.Измените высоту падения на 30-40см и повторите опыт. Полученные данные внесите в табл. I и 2.

3.2.9.По формуле (3.6), используя значения входящих парамет­ров, вычислите g.

3.2.10.Оцените точность определения g, для этого подсчи­тайте относительную и абсолютную ошибки соответственно по формулам:

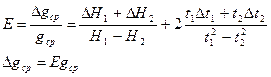
Результат представьте в виде g = (g_ср – Δg_ср) м/с².

3.2.11.По средним значениям g, t₁, t₂ подсчитайте скорости v₁, v₂ падения тела с высот Н₁ и Н₂, используя фор­мулу (3.1).

3.2.12.Подсчитайте потенциальную и кинетическую энергия для случаев падения с высот Н₁ и Н₂.

3.2.13.Убедитесь в правильности закона сохранения энергии.

В рассматриваемом случае разность между П на высоте Н и Т при Н = 0 будет близка к нулю.

Контрольные вопросы

1. Какое ускорение называется ускорением силы тяжести?

2. Покажите справедливость использования формулы в условиях данного опыта.

3. Сформулируйте закон всемирного тяготения.

4. Сформулируйте закон сохранения энергии.

5. Дайте понятие консервативной и диссипативной систем.

Литература

1. Зисман Г.А., Тодес О.М. Курс обшей физики, т.1 IМ.,1974, стр. 38-43.

2. Савельев И.В. Курс общей физики, т. I, стр. 98-99, 181, 184.

3. Яворский Б.М. и др. Курс физики, т. I, 1965, стр. 58-62, 94.

ЛАБОРАТОРНАЯ РАБОТА № 4

ИЗУЧЕНИЕ ОСНОВНОГО ЗАКОНА ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ С ПОМОЩЬЮ МАЯТНИКА ОБЕРБЕКА

Цель работы. Экспериментальная проверка второго закона Ньютона для вращательного движения.

Приборы и принадлежности:

1. Маятник Обербека,

2. Секундомер.

3. Линейка.

4. Штангенциркуль.

5. Технические весы.

6. Разновес.

4.1. Теоретическое введение

Рассмотрим основной закон динамики вращательного движения на примере тела, вращающегося с угловой скоростью ω и около оси 00₁.

Выберем произвольно некоторую точку массой m_i на рас­стоянии r_i. Все внутренние силы, действующие на нее, спроектируем на прямую, перпендикулярную радиусу r_i и обозначим F_iвн, проекцию всех внешних сил обозначим F_iвш.

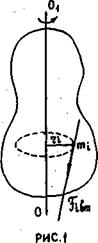Тогда в соответствии со вторым зако­ном механики для i -ой точки можно записать

m_i а_i = F_iвн + F_iвш, (4.1)

где а_i - линейное ускорение.

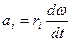(4.2)

Подставляя (2) в (I) и умножая пра­вую и левую части уравнения на r_i, будем иметь

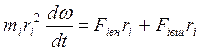(4.3)

Просуммируем (3) по всем точкам твердого тела

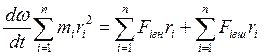(4.4)

Так как внутренние силы не могут вызвать вращения тела вокруг оси, то

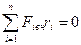(4.5)

и (4) запишется а виде

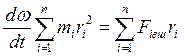(4.6)

Величина, определяемая произведением массы точки на квадрат рас­стояния до оси вращения, называется ее моментом инерции. Просум­мировав моменты инерции всех точек твердого тела, получаем момент инерции всего тела

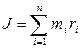(4.7)

Сумма в правой части формулы (6) представляет собой результирующий или главный момент внешних сил

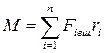(4.8)

Учитывая, что ускорение тела 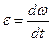, получим Основной закон динамики вращательного движения

Угловое ускорение при вращательном движении твердого тела прямо пропорционально результирующему моменту внешних сил и обратно пропорционально моменту инерции.

В данной работе нужно убедиться, что

I) при постоянном моменте инерции угловое ускорение прямо пропорционально главному моменту внешних сил;

2) при постоянном вращающем мо­менте угловое ускорение обратно пропорционально моменту инерции.

Основной закон динамики вращательного движения проверяет­ся на приборе, называемым маятником Обербека (рис. 2). Установка состоит из крестовины, на которой закрепляется равные грузы m₁, m₂, m₃, m₄. На оси имеется ступенчатый шкив (диаметры D₁ и D₂ ). Нить с грузом m наматывается на шкив, при опускания груза маятник приходит во вращательное движение под действием момента сил

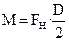, (4.10)

где

F_H = m(g – a), (4.11)

F_H – сила натяжения нити;

а – линейное ускорение груза;

g – ускорение свободного падения.

Или

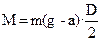(4.12)

Линейное ускорение определяется по времени перемещения гру­за m на некоторое расстояние h.

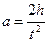(4.13)

С другой стороны, оно связано с угловым ускорением

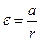(4.14)

4.2. Порядок выполнения работы

I часть: Момент инерции маятника постоянен (грузы, напри­мер, закреплены на концах крестовины). Меняем момент силы, пользуя то больший шкив, то меньший. Угловые ускорения должны меняться пропорционально вращающему моменту сил:

4.2.1.Взвесьте груз, m, результаты занесите в табл. I.

4.2.2.Закрепите грузы на концах (или середине), проверьте находится ли маятник в безразличном равновесии.

4.2.3.Намотайте нить сначала на малый шкив. Опустите груз и одновременно включите секундомер. Опыт повторите 3 раза с малым шкивом, потом с большим. Грузы не снимайте.

4.2.4.Произведения вычислите и убедитесь, что угловые ускорения пропорциональны моментам сил.

4.2.5.Измерьте штангенциркулем диаметр шкива D₁ и D₂ и линейкой.

Таблица I.

Шкив меньшего диаметра	N	m, кг	D, м	h, м	t, c	а, м/с2	ε,с-2	М, Н∙м	J, кг∙м2	М1/М2	ε 1/ ε 2
Ср
Шкив большего диаметра
Ср

II часть: Момент сил, действующих на маятник, неизменен (нить с грузом m наматывается только на один шкив), а грузы закрепляются последовательно на концах, середине, а затем снима­ются. Угловые ускорения должны изменяться обратно пропорционально моментам инерции.

4.2.6. Перенесите из табл.1 m, h, a, ε, M для того шкива, который выбран во второй части работы, в табл. 2.

4.2.7.Измерьте расстояние от оси до центра грузов r_i (можно измерить расстояние от оси до груза штангенциркулем - дли­ну груза, а затем взять сумму первой и половина второй измерен­ных величин). Результата занесите в табл. 3.

4.2.8.Сместите грузы на середину, добейтесь безразличного равновесия и снова измерьте r_i.

4.2.9.Опустите груз m и измерьте время падения. Резуль­таты занесите в табл. 2.

4.2.10.Освободите маятник от грузов, и вновь проделайте изме­рения.

4.2.11. Произведите вычисления. Убедитесь, что угловые ускорения обратно пропорциональны моментам инерции.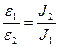

4.2.12. Момент инерции величина аддитивная. Поэтому момент инерции маятника с грузами равен сумме пустого маятника (экспери­ментальное значение из табл. 2), и 4-х грузов, которые можно при­нять за материальные точки. Сравните полученные значения моментов инерции с экспериментальными.

Таблица 2

Маятник	N	m, кг	D, м	t, c	а, м/с2	ε,с-2	М, Н∙м	J, кг∙м2	М1/М2	ε 1/ ε 2
Грузы на концах
Ср
Грузы на середине
Ср
Без грузов
Ср

Таблица 3

		ri	Момент инерции J, кг·м2
грузов	маятник с грузами (вычисле­ний)	маятник с грузами (экспери­ментальныq)
Грузы на середине
Грузы на концах

4.3. Контрольные вопросы

4.3.1.Какое движение называется вращательным?

4.3.2.Сформулируйте второй закон Ньютона для вращательного движения. Сравните с законом для поступательного движения.

4.3.3.Что такое момент инерции тела правильной формы обруча, цилиндра, шара, стержня?

4.3.4.Чему равен момент инерции системы тел?

4.3.5.Сформулируйте теорему Штейнера.

Литература

1. Савельев И.В. Курс общей физики, т. I, "Наука", М., 1977.

2. Физический практикум под редакцией профессора Ивероновой, "Наука", М., 1967.

ЛАБОРАТОРНАЯ РАБОТА № 5

ОПРЕДЕЛЕНИЕ МОМЕНТА ИНЕРЦИИ МАХОВОГО КОЛЕСА

ДИНАМИЧЕСКИМ МЕТОДОМ

Цель работы. Ознакомление с характеристиками и законами вращательного движения.

Приборы и материалы:

1. Маховое колесо.

2. Три груза.

3. Штангенциркуль.

4. Рулетка.

5. Секундомер.

5.1. Теоретическое введение

Вращательным называется такое движение, при котором все точки твердого тела описывают окружности, центры которых лежат на одной и той же прямой, называемой осью вращения.

Важнейшими характеристиками вращательного движения являются угловая скорость ω и угловое ускорение ε.

Угловой скоростью называется величина, равная изменению угла поворота твердого тела за единицу времени, т.е.

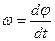(5.1)

Угловое ускорение описывает быстроту изменения угловой скорости:

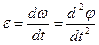(5.2)

При вращательном движении угловая скорость и угловое уско­рение для всех частиц твёрдого тела одинаковы. Линейная скорость υ точки вращающегося тела связана с угловой скоростью соотно­шением:

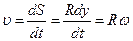(5.3)

где R - расстояние точки от оси вращения. Из этой формулы видно, что линейные скорости различных точек вращающегося тела различны.

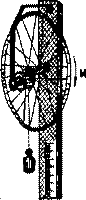Для описания динамики вращательного движения поня­тий силы и массы недостаточно. Действительно, если при по­ступательном движении опреде­ленная сила вызывает вполне определенные изменения движе­ния тела, то во вращательном движении результат действия силы зависит от того, на ка­ком расстоянии от оси враще­ния она приложена. Произведе­ние величины силы, приложен­ной к данной точке тела, на ее кратчайшее расстояние от оси вращения называется моментом силы.

M = F·r (5.4)

Произведение массы i-ой ма­териальной точки на квадрат расстояния ее до оси вращения называется моментом инерции материальной точки

Рис.1 J_i = m_i·r_i² (5.5)

Момент инерции всего тела равен сумме моментов инерции составляющих его материальных точек

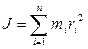(5.6)

Момент инерции характеризует инертность тела во вращательном движении и, как видно из (5.6), зависит от характера распределения массы относительно оси вращения r_i. По аналогии с поступательным движением, кинетическая энергия вращающегося тела равна:

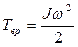(5.7)

Пусть твердое тело вращается под действием приложенной к нему силы F. (См. рис.I к лабораторной работе № 6). Рассмотрим достаточно малый промежуток времени t, такой, чтобы угловую скорость можно было считать постоянной. Тогда за время dt тело повернется с угловой скоростью ω на угол dJ = ωdt. При этом точка приложения силы описывает дугу dS = rdJ. Элементарная работа в этом случае равна

dA = FdS = FrdJ = Frωdt (5.8)

Эта работа идет на изменение кинетической энергии вращающегося тела, т.е.

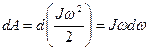(5.9)

Из равенства формул (5.8) и (5.9) следует

Frωdt = Jωdω (5.10)

Mdt = Jdωили Mdt = d(Jω)

Величина z = Jω называется моментом импульса (или моментом коли­чества движения). Произведение Mdt называется импульсом враща­ющего момента силы. Последнее выражение можно переписать в виде:

Mdt = dz (5.11)

т.е. импульс момента силы равен изменению момента импульса (мо­мента количества движения), вращающегося твердого тела. Это основ­ной закон динамики вращательного движения. Закону можно придать и другую формулировку. Из (5.10) следует, что отсюда

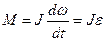(5.12)

т.е. угловое ускорение, приобретаемое телом под действием вращающего момента М, прямо пропорционально величине этого момента и обратно пропорционально моменту инерции тела Jотносительно оси вращения.

В настоящей работе, в качестве главного колеса, используется велосипедное, которое может вращаться вокруг горизонтальной оси, расположенной на высоте ~ 1,5 м от пола (см. рис. I). На оси колеса укреплен вал со шпилькой, на которую с помощью петли оде­вается шнур. К другому концу шнура привязан груз. Если вращать маховое колесо, то шнур накручивается на вал, в груз поднимается на некоторую высоту. В этом случае система получает некоторый запас потенциальной энергии, равный произведению веса груза на высоту подъема. Если затем опустить груз, то потенциальная энергия П будет превращаться в кинетическую энергию его поступательного движения Т пост, и энергию движения махового колеса Т пр. На основании закона сохранения энергии можно записать:

П = Т_пост – Т_вр (5.1З)

С учетом того, что П = mgh , 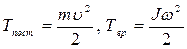уравнение (5.13) будет иметь вид

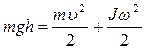(5.14)

Так как шнур намотан на вал, то скорость поступательного движения шнура и груза равна линейной скорости точек, лежащих на поверхности вала. Для её определения воспользуемся уравнени­ями равноускоренного движенья

υ = at и h = at²/2;

из которых

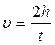(5.15)

Используя формулы (5.З) и (5.15) находим выражение для угловой скорости

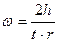(5.16)

Подставляем найденные значения υ и ω в (5.14) имеем:

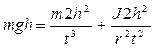(5.17)

После сокращения на h и элементарных преобразований получим расчетную формулу для определения момента инерции махового колеса:

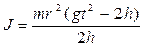(5.18)

Так как в работе удобно измерять не радиус, а диаметр D = 2r, формулу (5.18) можно записать в виде:

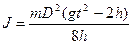(5.19)

5.2. Порядок выполнения работы

5.2.1.Взвесьте груз с помощью технических весов.

5.2.2.Измерьте штангенциркулем диаметр вала.

5.2.3.Измерьте высоту поднятия груза от подвижной планки, на которую ставится груз, до пола.

5.2.4.Наденьте петлю шнура на шпильку вала, намотайте на него шнур, поставьте груз на откидную планку. Нажав на пусковой механизм планки, одновременно пустите в ход секундомер, и измерьте время падения груза.

5.2.5.Опыт повторите 3 раза, и результаты измерений занесите в табл. I.

5.2.6.Подсчитайте по средним значениям измеряемых величин момент инерции махового колеса (формула № 19).

5.2.7.Определите относительную и абсолютную погрешности для получения значения момента инерции

Таблица I

	Высота подня­тия груза, (м)	Диаметр вала, (м)	Масса груза, (кг)	Время паде­ния груза, (с)
h	Δh	D	ΔD	m	Δm	t	Δt
Ср.

5.3. Контрольные вопросы

5.3.1.Какое движение называют вращательным?

5.3.2.Какие величины характеризуют вращательное движение?

5.3.3.В каких единицах измеряются угловая скорость и угловое ускорение?

5.3.4. Какая связь между линейными и угловыми скоростями и ускорениями.

5.3.5. Напишите и сформулируйте основной закон динамики вращательного движения?

5.3.6.Каков физический смысл инерции?

5.3.7.Приведите формулы моментов инерции некоторых тел правильной формы.

5.3.8.Выведите формулу (5.19).

Литература

1. Зисман Г.А., Тодес А.М. Курс общей Физики, т. I. "Наука", М., стр. 63-69.

2. Путилов В.А. Курс физики, ч.1, М., 1963, стр. 144-152.

3. Яворский Б.М. и др. Курс физики, ч. 1, 1965, стр. 66-74.

4. Фриш С.Э., Тиморева А.Е. Курс общей физики, т. I, М., 1963, стр. 12Т-129.

ЛАБОРАТОРНАЯ РАБОТА № 6

ОПРЕДЕЛЕНИЕ ДЛИНЫ ЗВУКОВОЙ ВОЛНЫ И СКОРОСТИ ЗВУКА ПО ФАЗОВЫМ СООТНОШЕНИЯМ

Цель работы: Изучение явления сложений колебаний. Определение скорости звука по фазовым соотношениям.

Приборы и принадлежности:

1. Звуковой генератор ЗГ-10.

2. Электронный осциллограф ЭО-7.

3. Громкоговоритель.

4. Микрофон.

5. Оптическая скамья с отсчетной шкалой.

6.1. Теоретическое введение

Если колебательная система находится в упругой среде (воздухе, воде или другом веществе), то частицы среды непосредственно при­легающие к ней, также будут совершать колебательные движения. А в результате упругого взаимодействия их с другими частицами последние начнут колебаться. Таким образом, колебания будут пере­даваться от одних частиц среды к другим и т.д.

Процесс распространения колебаний в среде называется волной. Каждая из частиц среды совершает колебания около положения устойчивого равновесия. При этом происходит передача энергии без переноса вещества.

Если колебания частиц происходят в направлении распространения волны, то такая волна называется продольной.

Если же колебания частиц перпендикулярны к направлению рас­пространения волны, то волна называется поперечной.

Поперечные волны возникают в результате деформации сдвига. Продольные в результате деформации сжатия и растяжения. Поэтому в твердом теле распространяются как продольные, так и поперечные волны. В жидкостях и газах могут распространяться только продольные волны, т.к. деформации сдвига в них не упруги.

Рассмотрим процесс распространения колебаний, источником которых являются точка 0 (рис. I), колеблющаяся по гармонически закону

x = Asinωt (6.1)

т.е. точки колеблются в одинаковых фазах, и мы можем дать другое определение длине волны. Расстояние между двумя ближайшими точка­ми, называется длиной волны, если точки колеблются в одинаковых фазах. Заметим также, что

υ ,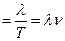

где 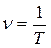- частота колебаний.

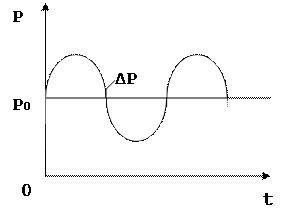
Звуковая волна в воздухе представляет собой чередующиеся в пространстве и во времени сжатия и разряжения воздуха. Давление воздуха при наличии в нем звукового процесса колеблется около среднего значения Р_о:

Р = Р_о +ΔР

Если источник звуковых волн совершает колебания по гармоническому закону (например, громкоговоритель, питаемый от звукового генера­тора), то и ΔР изменяется по тому же закону (см. рис. 2):

Δ Р = Δ Р_о sin(ω∙t - φ) (6.5)

Δ Р = Р_о + Δ Р_о sin(ω∙t - φ)

В данной работе мы будем заниматься исследованием "звукового поля". Источником звука служит громкоговоритель, питаемый от звукового генератора. Приемником служит микрофон.

Давление, создаваемое воздухом на мембрану микрофона, будет изменяться по гармоническому закону, следовательно, по гармони­ческому закону будет изменяться и напряжение в цепи микрофона.

Если электрические колебания, возникшие в цепи микрофона подать на вертикальные пластины осциллографа, а напряжение с клемм громкоговорителя на горизонтальные пластины, то в результате сложения двух взаимоперпендикулярных колебаний одинаковых частот на экране осциллографа получим траекторию результирующего колеба­ния, которая называется фигурой Лиссажу. В зависимости от соотноше­ния складываемых колебаний, фигура может быть в виде эллипса, окружности, прямой линии или носить более сложный характер.

В виду важности этого вопроса в данной работе рассмотрим его подробнее.

Траектория точки, участвующей в двух взаимоперпендикулярных

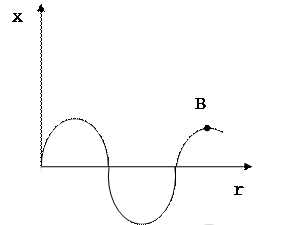x = A₁sin(ω∙t - φ₁);

y = A₂sin(ω∙t - φ₂).

В любой другой точке В, отстоящей от точки 0 на рас­стоянии r , ко­лебания будут происходить по тому же закону, но с запаздыванием на время

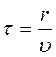
где υ - скорость распространения волны в данной среде. Тогда колебания точки будут описываться уравне­нием

рис1

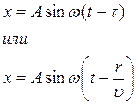(6.2)

Уравнение (6.2) называется уравнением бегущей волны, из которого
видно, что смещение каждой точки есть функция от расстояния до
источника и времени наблюдения.

Так как 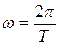, то уравнение (2) можно переписать в виде:

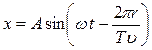
Расстояние, на которое распространяется волна за время, рав­ное одному периоду, называется длиной волны:

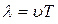(6.3)

С учетом (6.3) уравнение бегущей волны можно записать:

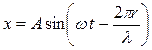(6.4)

Выражение 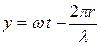- называется фазой волны.

Определим разность фаз двух колеблющихся точек, расположен­ных на одном и том же луче r, вдоль которого распространяется волна, разделенных расстоянием nλ, где n – 1,2,3…

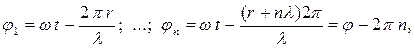
колебаниях

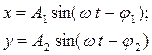
описывается уравнением:

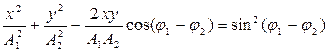
(6.6)

Это уравнение, в об­щем случае, является уравнением эллипса. Рассмотрим только несколько наиболее характерных случаев.

1.Разность фаз равна нулю или кратному 2π, т.е.

y₁ – y₂ = n2π

где n = 0,1,2,…

В этом случае (6.6) примет вид:

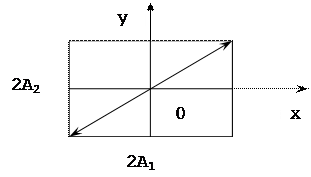
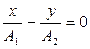или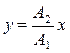

В данном случае тра­ектория точки, есть прямая, проходящая по первому и третьему квадратам, и является диагональю прямоуголь­ника со сторонами 2А₁ и 2А₂ (см. рис. 3).

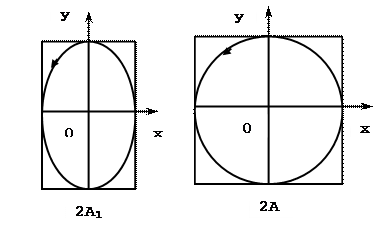
2. Разность фаз равна нечетному кратному π/2

Рис.3

где n = 0,1,2…

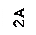
уравнение (6.6) примет вид: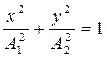

а) б) Рис.5

Рис.4

Это уравнение эллипса, для которого оси координат являются главны­ми осями. Точка движется по эллипсу по часовой стрелке (см. рис.4а). Если А₁ = А₂, то траектория точки - есть окружность (рис. 46).

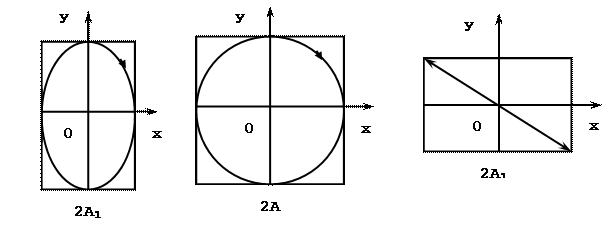
3. Разность фаз равна не­четному кратному ±π т.е.

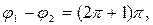
где n = 0,1,2…

Тогда из уравнения (6.6) имеем:

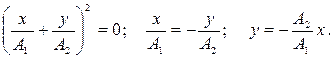
Это уравнение прямой, проходящей по второму и четвертому квадратам (Рис.5).

4.Разность фаз равна:

где n = 0,1,2…

Точка в этом случае движется по эллипсу против часовой стрел­ки (Рис. 6а). При А₁ = А₂, точка движется по окружности против часовой стрелки (Рис.6б).

Рис.6

Выше мы установили, что две точки "волнового поля", разделен­ные расстоянием nλ, колеблются в одинаковых фазах. Это значит, что если мы получим на экране осциллографа какую-либо фигуру Лиссажу и будем удалять микрофон от громкоговорителя, то мы снова увидим на экране ту же фигуру при перемещении микрофона на рассто­яния λ, 2λ, 3λ и т.д.

Если установить расстояние от микрофона, до громкоговорителя, затем передвинуть микрофон в новое положение так, чтобы фигура Лиссажу на экране сделала n полных оборотов и расстояние станет равным r_n, то можно определить длину звуковой волны:

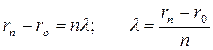(6.7)

Измерив длину звуковой волны λ при определенной частоте звукового генератора, можно определить скорость звука в воздухе:

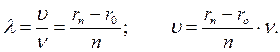(6.8)

6.2. Порядок выполнения работы

6.2.1.Собрать цепь по прилагаемой схеме (рис. 7).

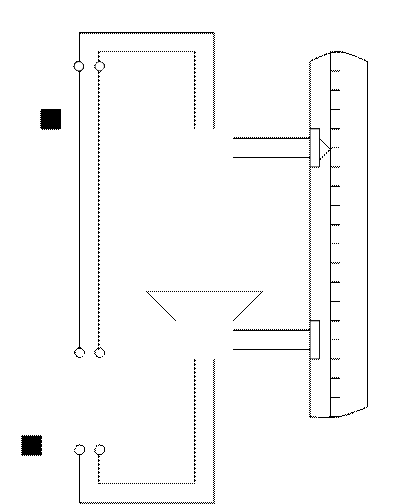6.2.2Подготовить установку к работе. Переключатель осцилло­графа поставить в положение "1:1", переключатель диапазона частот в положение "выкл. " Тумблер звукового генератора "внутренняя нагруз­ка" должен быть в положении "включено", входное сопротивление по­ставить 600 Ом, "затухание ДБ" в нулевое положение, множитель -"100".

6.2.3. Определить длину звуковой волны при заданной частоте генератора 2500Гц. Для этого установкой микрофона на самое близкое расстояние до громкоговорителя r₀, получить на экране осциллогра­фа прямую линию. Затем удалить микрофон так, чтобы фигура Лиссажу сделала 2-3 полных оборота и на экране осциллографа снова была та же прямая линия. Зная число полных оборотов фигуры на экране n и расстояние r_n – r₀, на которое передвинули микрофон по формуле (6.7) найти длину звуковой волны.

6.2.4.Установить микрофон на расстояния 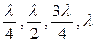и т.д., получить последовательность фигур Лиссажу и зарисовать их (значения взять из пункта 3).

6.2.5.Повторить измерения пункта 3 при известных частотах (3000, 3500, 4000) Гц.

6.2.6.Вычислить относительную и абсолютную погрешности измерений скорости звука

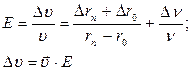(6.10)

6.3. Контрольные вопросы

6.3.1.Дайте определение волны.

6.3.2.Какие волны называются продольными, какие поперечными?

6.3.3.Введите уравнение бегущей волны.

6.3.4.Введите уравнение траектории точки, участвующей в двух взаимно перпендикулярных колебаниях одинакового периода.

6.3.5.Рассмотрите частные случаи уравнения (6.6).

6.3.6.Каким образом в работе определяется длина звуковой волны?

6.3.7.Получите формулу для определения скорости звука.

6.3.8.Исходя из формулы (6.8), найдите выражение для вычисления относительной погрешности (6.9).

Л и т е р а т у. р а

1. Горелик Г.С. Колебания волны.

2. Савельев И.В. Курс общей физики, ч. I, П., 1973.

ЛАБОРАТОРНАЯ РАБОТА № 7

ИЗУЧЕНИЕ ЗАТУХАЮЩИХ КОЛЕБАНИЙ

Цель работа. Определение параметров затухающих колебаний пружинного маятника.

Приборы и принадлежности:

1. Пружинный маятник.

2. Секундомер.

3. Набор грузов.

7.1. Теоретическое введение

Колебания, совершавшиеся без воздействия внешней периодической силы в результате какого-либо начального отклонения системы из поло­жения равновесия, называется свободными.

Если вследствие наличия сил трения амплитуда свободных колеба­ний с течением времени уменьшается, то такие колебания называются затухающими. Затухающие колебания, вообще говоря, не являются пери­одическими, т.к. максимальные значения смещения скорости и ускорения в них никогда не повторяются. Поэтому периодом затухающих колебаний принято называть время между двумя последовательными переходами системы положения равновесия при движении в одном и том же направле­нии.

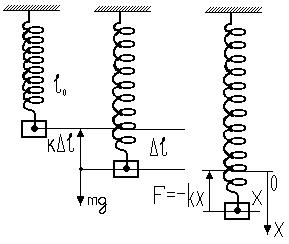Мы будем изучать затухающие колебания на примере пружинного маятника, представляющего собой груз массой m, колеблющейся на упругой пружине (рис. I).

Когда груз покоится на пружине, его вес уравновешивается силой упругости, обусловленной статическим изменением длины пружины Δℓ (Рис.1)

mg = k∙Δℓ,

где k – коэффициент упругости.

Если груз оттянуть на некоторое расстояние, то возникает возвращающая сила, пропорциональная смещению

F = - kx. (7.1)

Под действием этой силы груз будет совершать колебательное движение.

Рис.1 При небольших скоростях силы, вызывающие затухание, можно считать пропорциональными величине скорости

F = - r∙υ (7.2)

где r – коэффициент сопротивления. Знак «минус» указывает на то, что сила сопротивления направлена против смещения. Таким образом, мы приходим к дифференцированному уравнению затухающих колебаний:

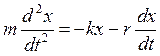
или

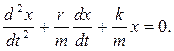(7.3)

Решение дифференциального уравнения (7.3) имеет вид:

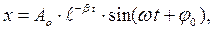(7.4)

где 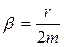- коэффициент затухания;

- циклическая частота затухающих колебаний;

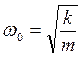- циклическая частота собственных колебаний.

Период затухающих колебаний определяется равенством:

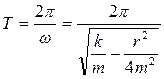(7.5)

Затухающие колебания можно рассматривать, как гармонические с изменяющейся по экспоненциальному закону амплитудой (Рис.2):

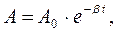
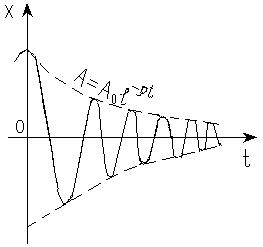(7.6)

где е = 2,718 – основание натуральных логарифмов.

Пусть в течение промежутка времени амплитуда затухающих колебаний уменьшается в ℓ раз:

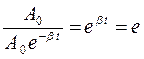
отсюда β∙τ = 1 или β = 1/τ (7.7)

Рис.2