Определение доверительных интервалов

Для построения доверительного интервала определяется предельная ошибка А для обоих показателей:

Формулы для нахождения доверительных интерваловвыглядят так

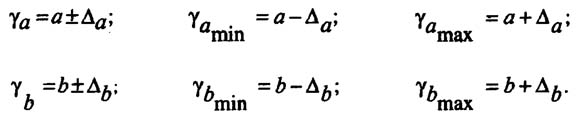
Прогнозное значение у определяется с помощью подстановки в уравнение регрессии прогнозного значения х. Вычисляется средняя стандартная ошибка прогноза

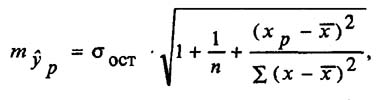
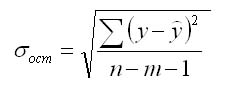
и находится доверительный интервал

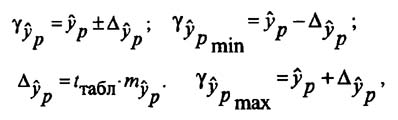
Задача регрессионного анализа в предмете эконометрика состоит в анализе дисперсии изучаемого показателя y:

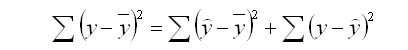
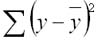общая сумма квадратов отклонений (TSS)

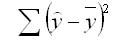сумма квадратов отклонений, обусловленная регрессией (RSS)

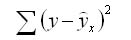остаточная сумма квадратов отклонений (ESS)

Долю дисперсии, обусловленную регрессией, в общей дисперсии показателя у характеризует коэффициент детерминации R, который должен превышать 50% (R² > 0,5). В контрольных по эконометрике в ВУЗах этот показатель рассчитывается всегда.

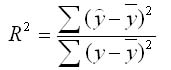
Любые задачи по эконометрике решаются здесь

Коэффициент детерминации - хаоактеризует долю дисперсии результативного признака у, объясняемую регрессией, в общей дисперсии результативного признака. Соответственно величина 1-r^2 характеризует долю дисперсии у, вызванную влиянием остальных не учтенных в модели факторов.

Мультиколлинеарностью для линейной множественной регрессии называется наличие линейной зависимости между факторными переменными, включёнными в модель.

Мультиколлинеарность – нарушение одного из основных условий, лежащих в основе построения линейной модели множественной регрессии.

Мультиколлинеарность в матричном виде – это зависимость между столбцами матрицы факторных переменных Х

Гомоскедастичность - дисперсия каждого Еi одинакова для всех значений x.

При малом объеме выборки для оценки нарушения гомоскедастичности можно использовать метод Гольдфельда-Квандта, который включает:

1.Упорядочение наблюдений n по мере возрастания переменной х.

2. Исключения из рассмотрения центральных наблюдений C; (n-C)/p при этом где p – число оцениваемых параметров.

3. Разделение совокупности (n-C) на две группы (с малыми и большими значениями фактора х) и определение по каждой из групп уравнений регрессии.

4. Определение остаточной суммы квадратов для обеих групп (S1) и (S2) и нахождение их отношения: R=S1/S2 При выполнении нулевой гипотезы о гомоскедастичности отношение R будет соответствовать F-критерию с (n-C-2p)/2 степенями свободы для каждой остаточной суммы квадратов. Чем больше величина R превышает табл. значение F-критерия, тем больше нарушена предпосылка о равенстве дисперсий остаточных величин.