Оценка производственной функции

ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ПО ЗЕМЛЕУСТРОЙСТВУ

КАФЕДРА ЗЕМЛЕУСТРОЙСТВА

ЭКОНОМИКО-МЕТЕМАТИЧЕСКИЕ МЕТОДЫ И МОДЕЛИРОВАНИЕ

ПРОИЗВОДСТВЕННЫЕ ФУНКЦИИ

Задания для выполнения лабораторных работ

Для студентов высших учебных заведений по специальностям:

Землеустройство

Земельный кадастр

Городской кадастр

и направлению:

Землеустройство и земельный кадастр

Москва - 2003

УДК 332.3:519.86

Подготовлены к печати кафедрой землеустройства Государственного университета по землеустройству (протокол № от 2003г)

Составители: проф. С.Н.Волков

доц. В.В.Бугаевская

Рецензенты:

ЗАДАНИЕ I

ИСПОЛЬЗОВАНИЕ ПРОИЗВОДСТВЕННЫХ ФУНКЦИЙ ПРИ РЕШЕНИИ ЗЕМЛЕУСТРОИТЕЛЬНЫХ ЗАДАЧ

Демонстрационная задача №1

При составлении задания на проектирование необходимо установить планируемую урожайность гречихи на расчетный 2010 год. По данным годовых отчетов имеется следующая фактическая урожайность гречихи (ц/га), представленная в таблице 1:

Таблица 1

Исходные данные к задаче 1

Годы	Порядковый номер года, (хj)	Фактическая урожайность, ц/га, (уj)
		8,8
		9,0
		10,4
		11,5
		11,0
		11,8
		12,0
		12,5
		13,0
		13,3
		13,5
		14,2

Необходимо установить имеется ли зависимость между значением урожайности гречихи и годами.

Решение задачи.

Для того чтобы понять имеется ли зависимость между значением урожайности и годами, построим график в двухмерной системе координат (x,y), где у – урожайность гречихи, х – годы (рис.1).

Графический способ представления исходной информации используется, когда важно не только значение производственного результата, но и направление и характер его изменения.

По графическому представлению (рис. 1), построенному по данным таблицы 1, можно предположить, что зависимость урожайности гречихи от времени носит линейный характер, тогда реальную зависимость можно заменить функциональной линейной связью: y=a₀+a₁x .

Для определения параметров a₀ и a₁ используем принцип наименьших квадратов.

y

	10,0

8,0

x

0 2 4 6 8 10

Рис. 1. Графическое представление зависимости урожайности от времени. Точками показаны результаты наблюдений.

Для получения системы нормальных уравнений приравняем нулю первые производные суммы квадратов отклонений случайных величин (у^j) от соответствующих значений уравнения регрессий 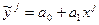по параметрам а₀ и а₁:

;

Получаем следующую систему нормальных уравнений:

;

;

.

В данных уравнениях величины и 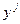- статистические данные, представленные в табл.1, а параметры a₀ и a₁ неизвестные величины, которые определим из решения двух уравнений с двумя неизвестными.

Для расчета коэффициентов системы нормальных уравнений а₀, а₁ составим таблицу 2.

Таблица 2

Расчёт коэффициентов системы нормальных уравнений

для расчета параметров «a₀» и «а₁» (случай линейного представления зависимости)

Годы (j)	хj	уj	(хj)2	хj уj	Ўj силаж Ўj=f(x)	(уj)2для расчёта rуx
		8,8		8,8	9,22	77,44
		9,0		18,0	9,68
		10,4		31,2	10,14	108,16
		11,5			10,60	132,25
		11,0			11,06
		11,8		70,8	11,52	139,24
		12,0		84,0	11,98
		12,6		100,0	12,44	156,25
		13,0			12,9
		13,3			13,36	176,89
		13,5		148,5	13,82	182,25
		14,2		170,4	14,28	201,64
∑				982,7		1689,12
( )2
∑/п		11,75

Таким образом линейное функциональное представление зависимости урожайности гречихи от времени примет вид:

ў=f(x)=8,76+0,46х

Подставляя в полученное уравнение значения (х^j), определим расчетную урожайность по годам (ў):

y₉₀=8,76+0,46∙1=9,22

y₉₁=8,76+0,46∙2=9,68

y₉₂=8,76+0,46∙3=10,14

y₉₃=8,76+0,46∙4=10,60

y₉₄=8,76+0,46∙5=11,06

у₂₀₀₁=8,76+0,46∙12=14,28

у₂₀₁₀=8,76+0,46∙21=18,42

Варианты расчета прогнозируемой урожайности для контроля:

у₂₀₁₀=у₁₉₉₅+0,46 ∙х_{2010 -1995}=11,52+0,46∙15=18,42.

Оценка производственной функции

Вычислим коэффициент корреляции, показывающий, насколько зависимость у^j= ^j, выраженная выборкой близка к линейной.

.

Область значений

Для вычисления коэффициента корреляции воспользуемся расчётами, проведёнными в табл.2.

,

.