Выбор интервалов варьирования.

После того, как определен основной уровень каждого Ф., необходимо выбрать два уровня, на которых он будет варьироваться в эксперименте. Один из этих уровней считается верхним, а второй нижним. Обычно за верхний уровень принимается тот, который соответствует большему значению фактора.

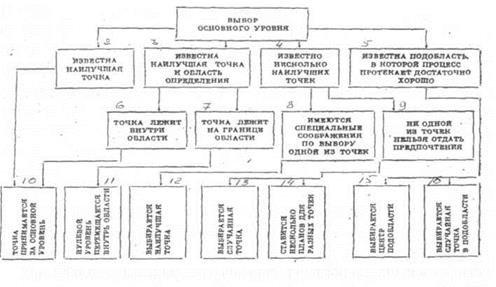Интервалом варьирования факторов называется некоторое число (свое для каждого фактора), прибавление которого к основному уровню дает верх­ний, а вычитание - нижний уровни фактора, т.е. интервал варьирования - это расстояние на координатной оси между основным и верхним либо нижним уровнями. Таким образом, задача выбора уровней сводится к более простой задаче выбора интервала варьирования.

Отметим еще, что для упрощения записи условий эксперимента и об­работки экспериментальных данных масштабы по осям выбираются так, чтобы верхний уровень соответствовал +1, нижний -1, а основной нулю. Для факторов с непрерывной областью определения это всегда можно сделать с помощью преобразования: 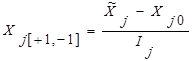, где Xj - кодирование значений Ф., 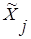- натуральное значение Ф.

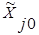-натуральное значение основного уровня.

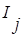- интервал варьирования.

j - номер фактора

Пример:

Факторы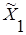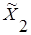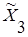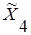
Основной уровень			1,5
Интервал варьирования

На выбор интервалов варьирования накладываются естественные огра­ничения сверху и снизу. Интервал варьирования не может быть меньше той ошибки 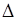, с которой эксперимент фиксирует уровень фактора. Иначе верхний и нижний уровни окажутся неразличимыми. С другой стороны, интервал не может быть настолько большим, чтобы верхний и нижний уровни оказались за пределами области определения.

При решении задачи оптимизации необходимо выбрать для первой се­рии экспериментов такую область, которая давала бы возможность для шаго­вого движения к оптимуму. В задачах интерполяции интервал варьирования охватывает всю описываемую область.

Выбор интервалов варьирования - задача трудная, т.к. она связана с неформализованным этапом планирования эксперимента. Возникает вопрос, какая априорная информация может быть полезна на данном этапе? Это - сведения о точности, с которой экспериментатор фиксирует значения факто­ров, о кривизне поверхности отклика и диапазоне изменения параметра оп­тимизации. Обычно эта информация является предварительной на первом этапе планирования эксперимента. В ходе эксперимента её приходится кор­ректировать.

Точность фиксирования факторов определяется точностью приборов и стабильностью уровня в ходе опыта. Кроме того, для интервалов вводится градация - широкий, средний и узкий интервалы варьирования.

Дополнительно: Полный факторный эксперимент

Эксперимент, в котором реализуются все возможные сочетания уровней факторов, называется полным факторным экспериментом. При числе уровней каждого фактора равного 2, имеем П.Ф.Э. типа 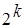. В табл.1. для со­ответствующего значения kуказано требующее число опытов N .

Таблица 1.

k
N

Факторы Опыты	X1	Х2
	- 1	- 1
	+ 1	- 1
	- 1	+ 1
	+ 1	+ 1

Условия эксперимента можно записать в виде таблицы, где строки со­ответствуют различным опытам, а столбцы — значениям факторов. Будем на­зывать такие таблицы матрицами планирования эксперимента (МПЭ). МПЭ для 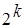факторов приведена ниже.

Существует несколько приемов записи МПЭ. Воспользуемся наиболее удобным: в первом столбце знаки меняются поочередно, во втором столбце они чередуются через 2, в третьем - через 4, в четвертом - через 8 и т.д.

Отметим ряд свойств, которыми обладает МПЭ. В данном случае мы возьмем те свойства, которые определяют качество модели, а это значит, что оценки коэффициентов модели должны быть наилучшими и что точность предсказания параметра оптимизации не должна зависеть от направления в факторном пространстве, т.к. заранее не ясно, куда предстоит двигаться в по­исках оптимума.

Два свойства следуют непосредственно из построения матрицы. Первое из них - симметричность относительно центра эксперимента - алгебраическая сумма элементов вектор столбца каждого фактора равна нулю, или 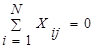, где j- номер фактора, N – число опытов, j=1,2,…,k.

Второе свойство - так называемое условие нормирование - формулиру­ется следующим образом: сумма квадратов элементов каждого столбца равна числу опытов т.е. 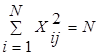Первые 2 свойства вытекают из отдельных столбцов МПЭ. Теперь отметим свойства, вытекающие из совокупности столбцов.

Третье, сумма почленных произведений любых 2х вектор столбцов МПЭ равных нулю: 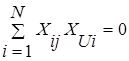. Это важное свойство называется ортогональностью МПЭ.

Четвертое, последнее свойство называется ротатабельностью, т.е. точки в матрице планирования подбираются так, что точность предсказания значений параметра оптимизации одинакова на равных расстояниях от центра экс­перимента и не зависит от направления.

Вернемся к матрице 2². для движения в точке оптимума воспользуемся линейной моделью 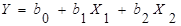. Наша цель - по результатам эксперимента найти коэффициент модели. В данном случае эксперимент проводится для проверки гипотезы о том, что модель 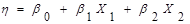адекватна, где 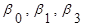- истинные значения соответствующих неизвестных, a 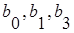- оценки 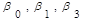. Коэффициенты модели вычисляются по очень простой формуле 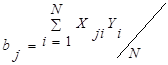, j=0,1,2,…,k.

Коэффициенты при независимых переменных указывают на силу влияния факто­ров. Чем больше численная величина коэффициента, тем большее влияние оказывает фактор. Если коэффициент имеет значок «+», то с увеличением зна­чения фактора параметр оптимизации увеличивается, если «-», то уменьшается.

Планируя эксперимент, на 1-ом этапе стремимся получить линейную модель. Однако нет гарантии в том, что в выбранных интервалах варьирования процесс описывается линейной моделью. А в случае, если модель нелинейна? Один из часто встречающихся видов нелинейности связан с тем, что эффект одного фактора зависит от уровня на котором находится другой фактор, т.е. присутствует эффект взаимодействия 2^-х факторов. П.Ф.Э. позволяет качест­венно оценить эффекты взаимодействия. Для этого надо, пользуясь правилом перемножения столбцов, получить столбец произведения 2^х факторов.

Реализация плана эксперимента

К проведению опытов необходимо тщательно подготовиться, собрать опытную установку, проверить и прокалибровать приборы, подготовить ис­ходное сырье, составить специальный журнал. Журнал оформляют в соответствии с методикой и планом опытов так, чтобы была ясна последовательность действий. На первой странице описывают цель исследований, параметр оптимизации и факторы с указанием их размерности. Желательно перечислить все факторы, которые могут служить
характеристиками процесса и указать, какая между ними существует корреляция. После этого необходимо перечислить основные факторы, указать их уровни и интервалы варьирования в виде таблицы. Целесообразно в рабочей матрице планирования проставлять не только кодовые значения факторов, но и натуральные. В рабочей матрице планирования необходимо оставить место для столбцов, в которых отмечаются даты постановки опытов и фамилий экспериментаторов. Затем, необходимо тщательно подготовить регистр, и измерить аппаратуру и сырье (оно должно быть однородным). Все
измерения и расчеты сохраняются в журнале до окончания работы (описание технологии, описание экспериментальной установки).