Сферическое движение твердого тела.
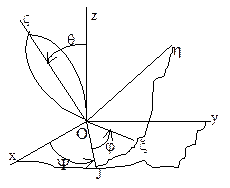 Сф.движ – движение твердого тела, одна из точек которого во все время движения остается неподвижной (напр. движение волчка). Точки тела движутся по сферическим поверхностям. Положение тела определяют при помощи трех углов. Для этого задаются две системы координат: неподвижная Оxyz и подвижная ОxhV, связанная с твердым телом. Линия ОJ – линия узлов, задаются углы: Y – угол прецессии, q – угол нутации, j – угол собственного вращения — углы Эйлера. Таким образом уравнения сферического движения: Y=f1(t); q=f2(t); j=f3(t). Углы отсчитываются от осей против хода час.стр. Теорема Эйлера-Даламбера: всякое перемещение тела, имеющего неподвижную точку, можно заменить одним поворотом вокруг
Сф.движ – движение твердого тела, одна из точек которого во все время движения остается неподвижной (напр. движение волчка). Точки тела движутся по сферическим поверхностям. Положение тела определяют при помощи трех углов. Для этого задаются две системы координат: неподвижная Оxyz и подвижная ОxhV, связанная с твердым телом. Линия ОJ – линия узлов, задаются углы: Y – угол прецессии, q – угол нутации, j – угол собственного вращения — углы Эйлера. Таким образом уравнения сферического движения: Y=f1(t); q=f2(t); j=f3(t). Углы отсчитываются от осей против хода час.стр. Теорема Эйлера-Даламбера: всякое перемещение тела, имеющего неподвижную точку, можно заменить одним поворотом вокруг
некоторой мгновенной оси вращения, проходящей через эту точку. Скорости всех точек тела, лежащих на мгновенной оси вращения в данный момент времени равны нулю. Вектор угловой скорости (мгновенной угловой скорости) откладывается о неподвижной точки по мгновенной оси в такую сторону, чтобы, смотря навстречу этому вектору, видеть вращение происходящим против час.стр. Вектор угловой 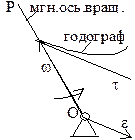 скорости со временем изменяется не только по численной величине, но и по направлению. Конец вектора описывает годограф скорости вектора
скорости со временем изменяется не только по численной величине, но и по направлению. Конец вектора описывает годограф скорости вектора  . Угловое ускорение:
. Угловое ускорение: 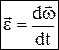 – скорость конца вектора
– скорость конца вектора 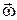 , совпадает по направлению с касательной к годографу вектора угловой скорости. В случае сферич. движение в отличии от случая вращения вокруг неподвижной оси вектор
, совпадает по направлению с касательной к годографу вектора угловой скорости. В случае сферич. движение в отличии от случая вращения вокруг неподвижной оси вектор 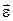 не совпадает с направлением
не совпадает с направлением 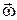 . Скорости точек при сферич. движ.:
. Скорости точек при сферич. движ.: 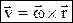 – векторное произведение,
– векторное произведение, 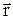 – радиус-вектор точки, проведенный из неподвижной точки, модуль v=wr×sina=w×h, h– расстояние от точки до мгновенной оси вращения. Формулы Эйлера:
– радиус-вектор точки, проведенный из неподвижной точки, модуль v=wr×sina=w×h, h– расстояние от точки до мгновенной оси вращения. Формулы Эйлера: 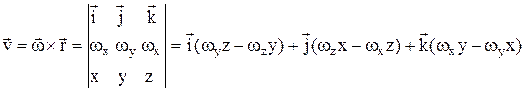 .
.
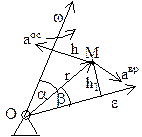 Ускорения:
Ускорения: 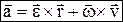 , вращательное ускорение
, вращательное ускорение 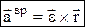 модуль вращат. уск. авр=e×r×sinb=e×h1, h1– расстояние от точки до вектора
модуль вращат. уск. авр=e×r×sinb=e×h1, h1– расстояние от точки до вектора 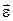 , направлено ^–но плоскости, проходящей через точку М и вектор
, направлено ^–но плоскости, проходящей через точку М и вектор 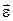 . Осестремительное ускорение
. Осестремительное ускорение 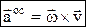 , аос=w2×h, направлено к оси вращения.
, аос=w2×h, направлено к оси вращения.
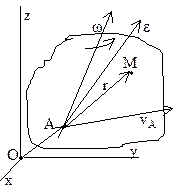 Движение свободного тв.тела (общий случай движения). Свободное тв.тело имеет шесть степеней свободы. При рассмотрении движения св.тв.тела, кроме неподвижной системы координат Oxyz, вводится подвижная система координат Ax1y1z1, которая связана с телом в точке А. Тогда движ. св.тв.тела представляет собой сложное движение, которое можно рассматривать как состоящее из поступательного движения вместе с полюсом (А) и сферич. движ. вокруг полюса. Ур-ия движ.св.тв.тела: xA=f1(t); yA=f2(t); zA=f3(t); Y=f4(t); q=f5(t); j=f6(t) (углы Эйлера). Первые три ур-ия определяют поступательную часть движ. и зависят от выбора полюса, остальные три определяют сферич. движ. вокруг полюса и от выбора полюса не зависят. Скорость любой точки св.тв.тела = геометрической сумме скорости полюса и скорости этой точки в ее сферическом движении вокруг полюса.
Движение свободного тв.тела (общий случай движения). Свободное тв.тело имеет шесть степеней свободы. При рассмотрении движения св.тв.тела, кроме неподвижной системы координат Oxyz, вводится подвижная система координат Ax1y1z1, которая связана с телом в точке А. Тогда движ. св.тв.тела представляет собой сложное движение, которое можно рассматривать как состоящее из поступательного движения вместе с полюсом (А) и сферич. движ. вокруг полюса. Ур-ия движ.св.тв.тела: xA=f1(t); yA=f2(t); zA=f3(t); Y=f4(t); q=f5(t); j=f6(t) (углы Эйлера). Первые три ур-ия определяют поступательную часть движ. и зависят от выбора полюса, остальные три определяют сферич. движ. вокруг полюса и от выбора полюса не зависят. Скорость любой точки св.тв.тела = геометрической сумме скорости полюса и скорости этой точки в ее сферическом движении вокруг полюса. 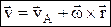
Ускорение точки св.тв.тела = геометрической сумме ускорения полюса, осестремительного ускорения точки и ее вращательного ускорения, определенных относительно мгновенной оси и оси углового ускорения, проходящих через полюс.
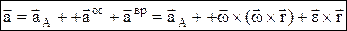 , два последних члена дают ускорение точки в ее движении вокруг полюса.
, два последних члена дают ускорение точки в ее движении вокруг полюса.
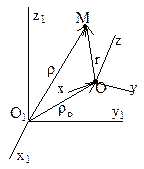 Сложное движение точки (тела) – такое движение, при котором точка (тело) одновременно участвует в нескольких движениях (напр. пассажир, перемещающийся по движущемуся вагону). В этом случае вводится подвижная система координат (Oxyz), которая совершает заданное движение относительно неподвижной (основной) системы координат (O1x1y1z1). Абсолютным движением точки назыв. движение по отношению к неподвижной системе координат. Относительное движение – движение по отношению к подвижной системе коорд. (движение по вагону). Переносное движение – движение подвижной сист. координат относительно неподвижной (движение вагона). Теорема о сложении скоростей:
Сложное движение точки (тела) – такое движение, при котором точка (тело) одновременно участвует в нескольких движениях (напр. пассажир, перемещающийся по движущемуся вагону). В этом случае вводится подвижная система координат (Oxyz), которая совершает заданное движение относительно неподвижной (основной) системы координат (O1x1y1z1). Абсолютным движением точки назыв. движение по отношению к неподвижной системе координат. Относительное движение – движение по отношению к подвижной системе коорд. (движение по вагону). Переносное движение – движение подвижной сист. координат относительно неподвижной (движение вагона). Теорема о сложении скоростей: 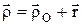 ,
, 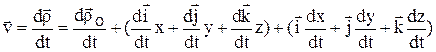 ;
; 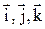 -орты (единичные вектора) подвижной системы координат, орт вращается вокруг мгновенной оси, поэтому скорость его конца
-орты (единичные вектора) подвижной системы координат, орт вращается вокруг мгновенной оси, поэтому скорость его конца 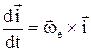 и т.д., Þ:
и т.д., Þ: 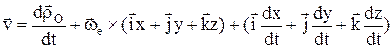 ,
,
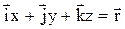 ;
; 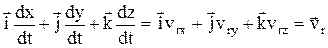 – относительная скорость.
– относительная скорость.
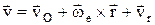 ; переносная скорость:
; переносная скорость: 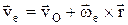 , поэтому абсолютная скорость точки = геометрической сумме ее переносной (ve) и относительной (vr) скоростей
, поэтому абсолютная скорость точки = геометрической сумме ее переносной (ve) и относительной (vr) скоростей 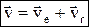 , модуль:
, модуль: 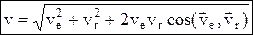 . Теорема о сложении ускорений (теорема Кориолиса):
. Теорема о сложении ускорений (теорема Кориолиса): 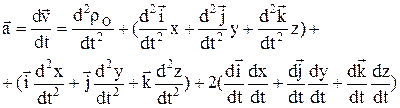
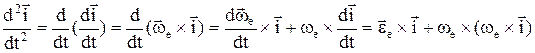 и т.д. Слагаемые выражения, определяющего ускорения
и т.д. Слагаемые выражения, определяющего ускорения 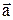 : 1)
: 1) 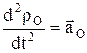 – ускорение полюса О;
– ускорение полюса О;
2) 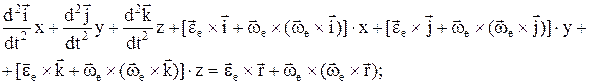
3) 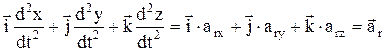 – относительное ускорение точки;
– относительное ускорение точки;
4) 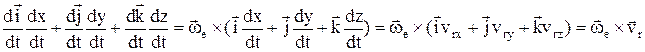 ,
,
получаем: 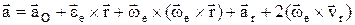 .
.
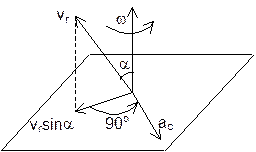 Первые три слагаемых представляют собой ускорение точки в переносном движении:
Первые три слагаемых представляют собой ускорение точки в переносном движении: 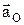 – ускорение полюса О;
– ускорение полюса О; 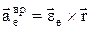 – вращательное уск.,
– вращательное уск., 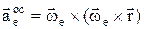 – осестремительное уск., т.е.
– осестремительное уск., т.е. 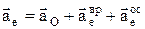 . Теорема о сложении ускорений (теорема Кориолиса):
. Теорема о сложении ускорений (теорема Кориолиса): 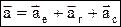 , где
, где 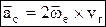 – ускорение Кориолиса (кориолисово ускорение) – в случае непоступательного переносного движения абсолютное ускорение = геометрической сумме переносного, относительного и кориолисова ускорений. Кориолисово ускорение характеризует: 1) изменение модуля и направления переносной скорости точки из-за ее относительного движения; 2) изменение направления относительной скорости точки из-за вращательного переносного движения. Модуль ускорения Кориолиса: ас= 2×|we×vr|×sin(we^vr), направление вектора
– ускорение Кориолиса (кориолисово ускорение) – в случае непоступательного переносного движения абсолютное ускорение = геометрической сумме переносного, относительного и кориолисова ускорений. Кориолисово ускорение характеризует: 1) изменение модуля и направления переносной скорости точки из-за ее относительного движения; 2) изменение направления относительной скорости точки из-за вращательного переносного движения. Модуль ускорения Кориолиса: ас= 2×|we×vr|×sin(we^vr), направление вектора 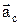 определяется по правилу векторного произведения, или по правилу Жуковского: проекцию относительной скорости на плоскость, перпендикулярную переносной угловой скорости, надо повернуть на 90о в направлении вращения.
определяется по правилу векторного произведения, или по правилу Жуковского: проекцию относительной скорости на плоскость, перпендикулярную переносной угловой скорости, надо повернуть на 90о в направлении вращения.
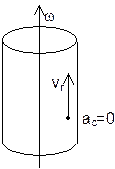 Кориолисово уск. = 0 в трех случаях: 1) we=0, т.е. в случае поступательного переносного движения или в момент обращения угл. скорости в 0; 2) vr=0; 3) sin(we^vr)=0, т.е. Ð(we^vr)=0, когда относительная скорость vr параллельна оси переносного вращения. В случае движения в одной плоскости – угол между vr и вектором we = 90о, sin90o=1, ас=2×we×vr.
Кориолисово уск. = 0 в трех случаях: 1) we=0, т.е. в случае поступательного переносного движения или в момент обращения угл. скорости в 0; 2) vr=0; 3) sin(we^vr)=0, т.е. Ð(we^vr)=0, когда относительная скорость vr параллельна оси переносного вращения. В случае движения в одной плоскости – угол между vr и вектором we = 90о, sin90o=1, ас=2×we×vr.
