Ауыстырулар жиынын ішкі жиындарға бөліктеу
Айталық  – бекітілген нөмірлер жүйесі және
– бекітілген нөмірлер жүйесі және  - қосымша нөмірлер жүйесі болсын. Демек,
- қосымша нөмірлер жүйесі болсын. Демек,  .
.  қосымша нөмірлер жүйесі бар кез келген
қосымша нөмірлер жүйесі бар кез келген  нөмірлер жүйесін алайық және төмендегідей
нөмірлер жүйесін алайық және төмендегідей  дәрежелі ауыстыруларды қарастырамыз:
дәрежелі ауыстыруларды қарастырамыз:

Барлық осындай бекітілген  ауыстырулар жиынын
ауыстырулар жиынын

деп белгілейік. Кез келген  нөмірлер жүйесіне
нөмірлер жүйесіне

санын сәйкес қояйық.
Лемма 1. Бекітілген  жүйесінде
жүйесінде  ішкі жиыны әр түрлі
ішкі жиыны әр түрлі  үшін қиылыспайды және олардың бірігуі барлық
үшін қиылыспайды және олардың бірігуі барлық 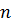 дәрежелі ауыстырулар жиынын береді. Егер
дәрежелі ауыстырулар жиынын береді. Егер  болса, онда
болса, онда

болады.
Лаплас теоремасы. Айталық  –
– 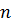 өлшемді квадрат матрица болсын.
өлшемді квадрат матрица болсын.  деп алып, кез келген
деп алып, кез келген 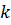 бағандардың жүйесін бекітейік. Онда
бағандардың жүйесін бекітейік. Онда  матрицасының анықтауышын есептеу бекітілген
матрицасының анықтауышын есептеу бекітілген 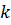 бағанның минорын және оның қосымша минорын есептеуге әкеледі:
бағанның минорын және оның қосымша минорын есептеуге әкеледі:

Дәлелдеуі. 1-лемманың негізінде мынаны аламыз:


Бірінші және екінші жақша сәйкесінше  және
және  береді.
береді.
(  шамасын
шамасын  минорының алгебралық толықтауышы деп атайды. Осылайша, Лаплас теоремасы былай тұжырымдалады, кез келген бағандар жүйесін таңдап алғанда матрицаның анықтауышы, берілген бағандарда орналасқан барлық мүмкін минорлардың, олардың алгебралық толықтауышына көбейтілген қосындысына тең.
минорының алгебралық толықтауышы деп атайды. Осылайша, Лаплас теоремасы былай тұжырымдалады, кез келген бағандар жүйесін таңдап алғанда матрицаның анықтауышы, берілген бағандарда орналасқан барлық мүмкін минорлардың, олардың алгебралық толықтауышына көбейтілген қосындысына тең.
 болғандықтан, онда Лаплас теоремасын былай да тұжырымдауға болады: кез келген жолдар жүйесін таңдап алғанда матрицаның анықтауышы, берілген жолда орналасқан, барлық мүмкін минорлардың, олардың алгебралық толықтауышына көбейтілген қосындысына тең.
болғандықтан, онда Лаплас теоремасын былай да тұжырымдауға болады: кез келген жолдар жүйесін таңдап алғанда матрицаның анықтауышы, берілген жолда орналасқан, барлық мүмкін минорлардың, олардың алгебралық толықтауышына көбейтілген қосындысына тең.
Блокты-үшбұрышты матрица анықтауышы
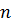 ретті блокты-үшбұрышты матрицаны қарастырайық:
ретті блокты-үшбұрышты матрицаны қарастырайық:

Алғашқы 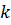 бағанның (немесе жолдың) жүйесі үшін Лаплас теоремасының қолданылуы келесі маңызды формуланы береді:
бағанның (немесе жолдың) жүйесі үшін Лаплас теоремасының қолданылуы келесі маңызды формуланы береді:
 .
.
ДӘРІС 9, 10
СКЕЛЕТТІК ЖІКТЕУ
Айнымалыларды ажырату және матрицалар
Екі айнымалының функциясын оқыған кезде айнымалысы ажыратылған 
функциясының немесе мынадай функциялардың қосындысы түріндегі

айнымалысы ажыратылған функциялардың маңызы зор.
Айталық  өлшемді матрица берілсін. Оның
өлшемді матрица берілсін. Оның  элементтерін
элементтерін  дискретті айнымалыларынан алынған функция ретінде қарастыруға болады. Бұл жағдайда айнымалыларды ажырату дегеніміз,
дискретті айнымалыларынан алынған функция ретінде қарастыруға болады. Бұл жағдайда айнымалыларды ажырату дегеніміз,  білдіреді.
білдіреді.
Бұдан  жол мен бағанның көбейтіндісі болатындығы шығады:
жол мен бағанның көбейтіндісі болатындығы шығады:
 ,
,  .
.
Скелеттік жіктеу
Айталық,  болсын. Бұл жерде
болсын. Бұл жерде  – «бағанды жолға» түріндегі
– «бағанды жолға» түріндегі  матрицалардың қосындысы:
матрицалардың қосындысы:

Ал бұл екі матрицаның көбейтіндісі түріндегі теңдікті береді:

 (*)
(*)
бұны  матрицасының скелеттік жіктелуі деп атайды. Яғни
матрицасының скелеттік жіктелуі деп атайды. Яғни  матрицасының әрбір бағаны
матрицасының әрбір бағаны  матрицасының бағанының сызықты комбинациясын, ал
матрицасының бағанының сызықты комбинациясын, ал  матрицасының әрбір жолы
матрицасының әрбір жолы  матрицасының жолының сызықты комбинациясын құрайды дегенді білдірерді. Бұдан келесі теорема шығады.
матрицасының жолының сызықты комбинациясын құрайды дегенді білдірерді. Бұдан келесі теорема шығады.
Теорема. 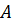 матрицасының бағанына созылған сызықты қабықшаның өлшемі оның жолына созылған сызықтық қабықшаның өлшемімен сәйкес келеді:
матрицасының бағанына созылған сызықты қабықшаның өлшемі оның жолына созылған сызықтық қабықшаның өлшемімен сәйкес келеді:
 .
.
