Потенциальная диаграмма для контура CRBAELDC

РГУ НЕФТИ И ГАЗА ИМ. И.М.ГУБКИНА

Кафедра ТЭЭП

ДОМАШНЕЕ ЗАДАНИЕ №1.

“Расчет линейной электрической цепи постоянного тока”

Группа РН-11-03,

Фамилия Тропин,

Имя Владислав.

Вариант №19

ПреподавательФедоришин В.В

Дата выдачи домашнего задания 14.02.2013______________

Дата сдачи домашнего задания .03.2013 ___________

Выполнил студент

(подпись)

ПринялОценка

(подпись) (зачет или оценка)

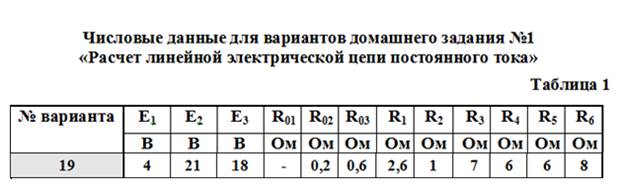
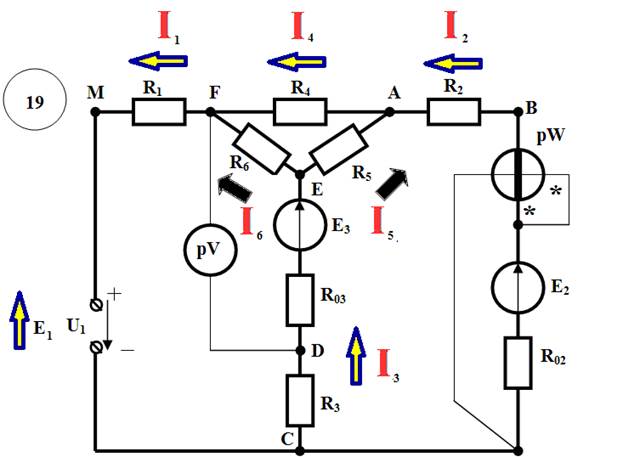
Решение:

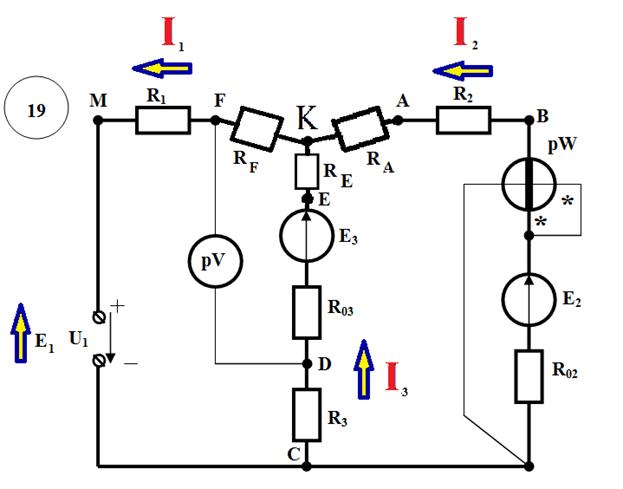
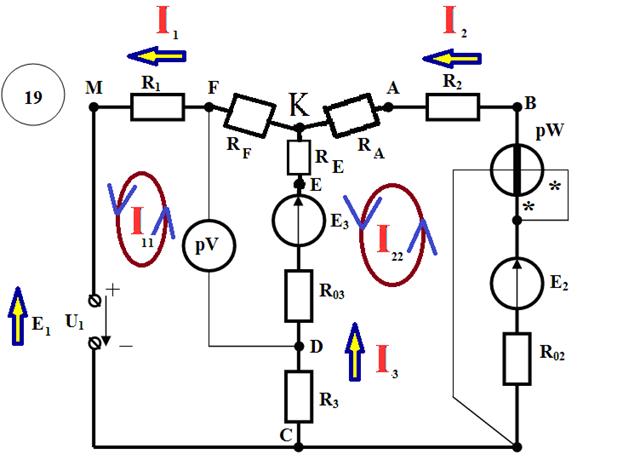
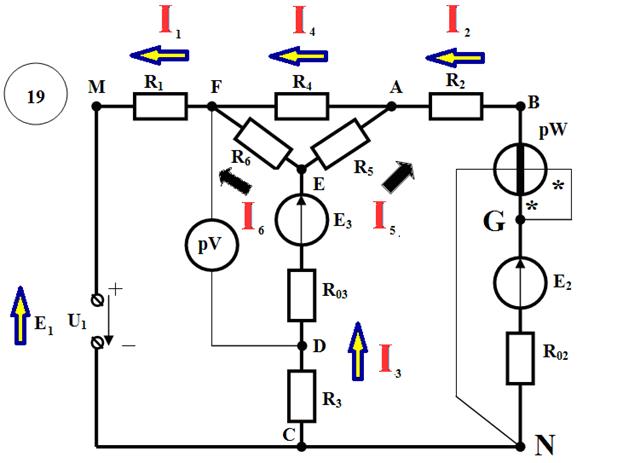
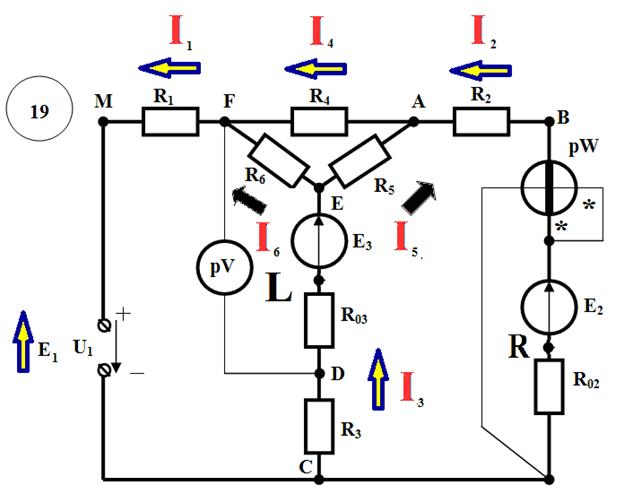
Указываем на схеме произвольно выбранные направления токов в ветвях, а также направление ЭДС идеального источника.

1.Число узлов: У=4 (F,A, E,C)

2.Число ветвей: В=6 (MF,FE,FA,AE,AC,EC)

Составление системы уравнений, необходимой для определения токов по первому и второму законам Кирхгофа.

I закон Кирхгофа

По первому закону Кирхгофа можем составить ( У-1) уравнение в нашем случае имеем

У-1=3 уравнения

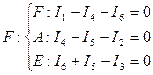
II закон Кирхгофа

По второму закона Кирхгофа можем составить К= В-У+1 уравнения , 6-4+1=3 уравнения.

Направление обхода во всех контурах – против часовой стрелки.

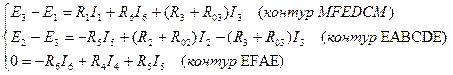
Преобразуем из треугольника в звезду контур AEF и выполним решение методом двух узлов.

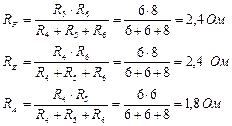
Преобразованная схема имеет вид:

Расчет токов в ветвях преобразованной схемы методом двух узлов

Вначале определим падение напряжений между двумя узлами K и C по формуле:

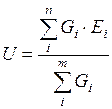, где 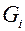- электрические проводимости соответствующих ветвей:

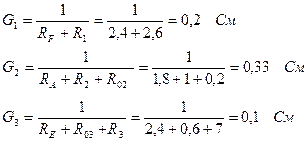
Тогда:

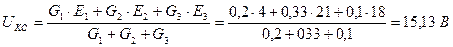
Рассчитаем неизвестные токи I₁, I₂, I₃ по обобщенному закону Ома:

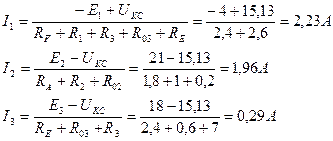
Определение токов через резисторы R₄, R₅, R₆

Для этого вернемся к исходной схеме и предварительно найдем значения потенциалов точек A, E, F ( , , ).

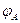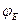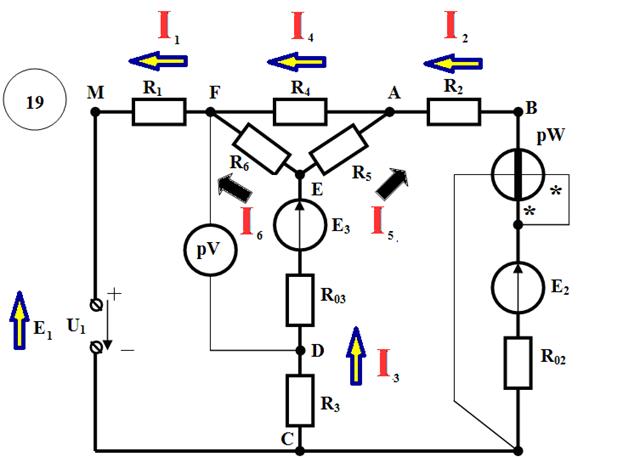
Если один из потенциалов схемы считать условно равным нулю, то схема не изменится. Предположим, φ_K=0. Тогда

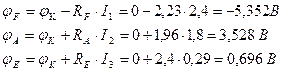
Зная разность потенциалов на участках цепи, найдем неизвестные значения токов по закону Ома:

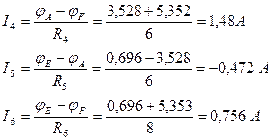
Первая предварительная проверка (по первому закону Кирхгофа):

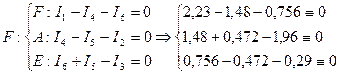
Вторая предварительная проверка (по второму закону Кирхгофа):

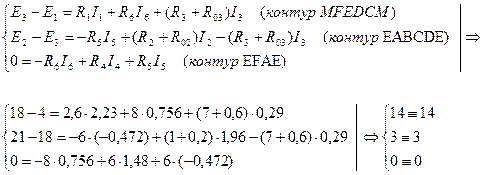
Расчет токов методом контурных токов

Поскольку в расчетной схеме два независимых контура (контур CMFKEDC и контур CDEKABC), то контурных тока будет также два: I₁₁ и I₂₂. Выберем произвольным образом направления токов, например, против часовой стрелки. Составим два линейных уравнения относительно неизвестных контурных токов I₁₁ и I₂₂, используя второй закон Кирхгофа:

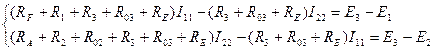
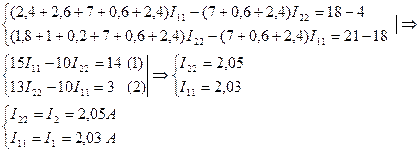
Вывод: как показывают расчеты, правильное применение различных методов расчета, дает один и тот же искомый результат.

Определение режимов работы источников ЭДС

Если направление ЭДС и направление тока совпадают, то источник ЭДС работает как генератор.

Если направление ЭДС и направление тока не совпадают, то источник ЭДС работает как потребитель (например, как аккумулятор).

Так как источник ЭДС Е₁ идеальный, то его КПД η₁=100%, работает как потребитель ( )*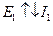

Чтобы найти КПД неидеальных источников, воспользуемся формулой:

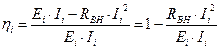
Тогда для первого неидеального источника:

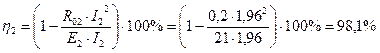, работает как генератор ( )*

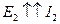Для третьего неидеального источника:

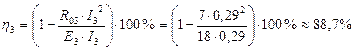, работает как генератор ( )*

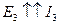* ЭДС определяют как работу сторонних сил, присущих источнику, на перемещение единичного положительного заряда внутри источника от зажима с меньшим потенциалом к зажиму с большим потенциалом,т.е.еслиЭДС направлена в направлении возрастания потенциалов ( 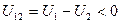) на участке цепи, то источник работает, как генератор:

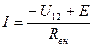
В противном же случае, источник работает, как аккумулятор:

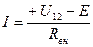
Баланс мощностей

Для составления баланса мощностей воспользуемся формулой:

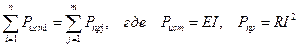
С учетом истинных направлений токов баланс мощностей для исходной схемы будет выглядеть следующим образом:

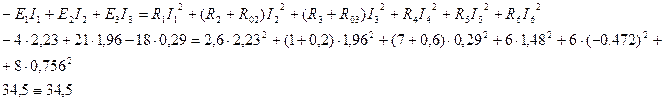
Определение показаний приборов

Для определения показаний приборов вернемся к первоначальной схеме.

Показания вольтметра pV определим через электрические потенциалы. Предположим, что

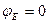. Тогда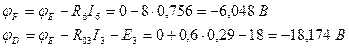

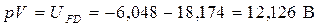
Проверка: по второму закону Кирхгофа (контур MCDEFM, обход против часовой стрелки)

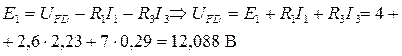
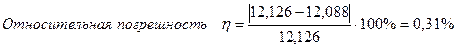
Для измерения мощности, потребляемой каким либо элементом цепи, необходимо, чтобы измерительный прибор измерял падение напряжения на нем и ток через него и перемножал эти значения:

Показания ваттметра pW определим по формуле:

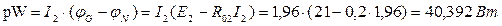
Проверка:

Мощность, поглощаемая (т.к. источник 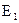работает , как аккумулятор) источником в цепи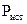

Вычисляется по формуле: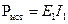

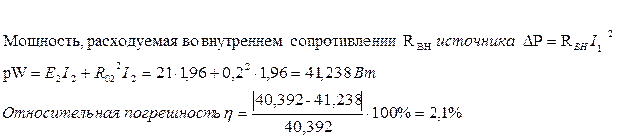
Построение потенциальной диаграммы

Выберем такой произвольный контур, в котором содержится хотя бы 2 источника ЭДС Е, например, CRBAELDC. Предположим, что φ_С=0. Тогда

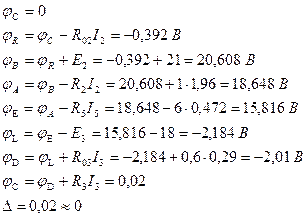
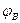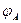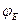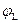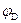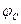Потенциал, B		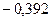		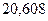	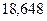15,816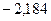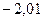
Сопротивление, Ом		0,2	0,2	1,2	7,2	7,2	7,8	15,8

Потенциальная диаграмма для контура CRBAELDC

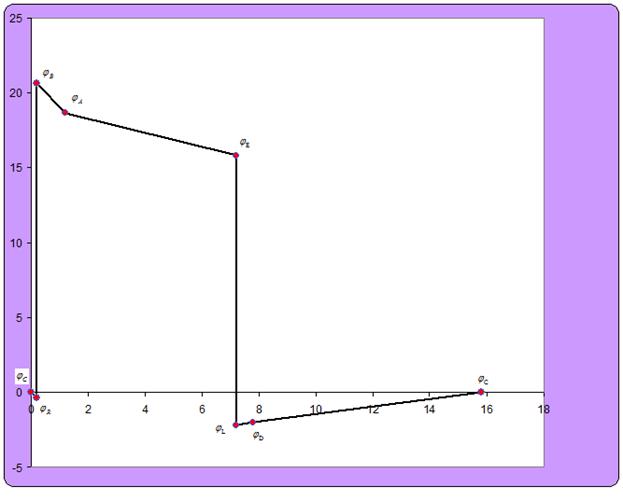
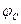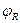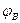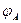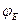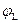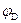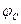Потенциал, B		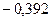		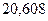	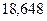15,816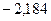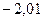
Сопротивление, Ом		0,2	0,2	1,2	7,2	7,2	7,8	15,8

Из графика видно, что независимый контур CRBAELDC замкнутый

Список использованной литературы

1. Федоришин В.В., Новоселова Ю.В. Методики решения задач линейных цепей постоянного тока. –М.: РГУ нефти и газа им.И.М.Губкина, 2004, 49с.

2. Касаткин А.С., Немцов М.В. Электротехника: Учебное пособие для вузов.

–М.: Энергоатомиздат, 1983, 440с.

3. http://www.exponenta.ru/

4. Конспекты лекций