Дискретная случайная величина и ее числовые характеристики

Дискретными случайными величинами называются случайные величины, принимающие только отдаленные друг от друга значения, которые можно заранее перечислить.
Закон распределения
Законом распределения случайной величины называется соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими им вероятностями.
Рядом распределения дискретной случайной величины называют перечень ее возможных значений и соответствующих им вероятностей.
Функцией распределения дискретной случайной величины называют функцию:
,
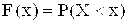определяющую для каждого значения аргумента x вероятность того, что случайная величина X примет значение, меньшее этого x.

Математическое ожидание дискретной случайной величины
,
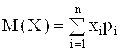где 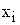- значение дискретной случайной величины; 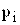- вероятности принятия случайной величиной X значений .
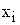Если случайная величина принимает счетное множество возможных значений, то:
.
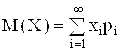Математическое ожидание числа наступлений события в n независимых испытаниях:
,
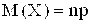где p - вероятность наступления события.
Дисперсия и среднеквадратическое отклонение дискретной случайной величины
Дисперсия дискретной случайной величины:
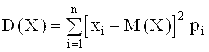или .
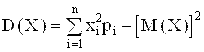Дисперсия числа наступлений события в n независимых испытаниях
,
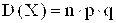где p - вероятность наступления события.
Среднеквадратическое отклонение дискретной случайной величины:
.

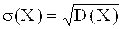Пример 1
Составьте закон распределения вероятностей дискретной случайной величины (д.с.в.) X – числа k выпадений хотя бы одной «шестерки» в n = 8 бросаниях пары игральных кубиков. Постройте многоугольник распределения. Найдите числовые характеристики распределения (моду распределения, математическое ожидание M(X), дисперсию D(X), среднее квадратическое отклонение s(X)).Решение: Введем обозначение: событие A – «при бросании пары игральных кубиков шестерка появилась хотя бы один раз». Для нахождения вероятности P(A) = p события A удобнее вначале найти вероятность P(Ā) = q противоположного события Ā – «при бросании пары игральных кубиков шестерка не появилась ни разу».
Поскольку вероятность непоявления «шестерки» при бросании одного кубика равна 5/6, то по теореме умножения вероятностей
P(Ā) = q = = .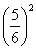
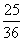Соответственно,
P(A) = p = 1 – P(Ā) = .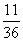
Испытания в задаче проходят по схеме Бернулли, поэтому д.с.в. величина X – число kвыпадений хотя одной шестерки при бросании двух кубиков подчиняется биномиальному закону распределения вероятностей:

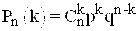
где 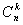= 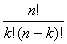– число сочетаний из n по k.

Проведенные для данной задачи расчеты удобно оформить в виде таблицы:
Распределение вероятностей д.с.в. X º k (n = 8; p = 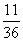; q = )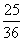

k										Сумма
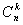Pn(k)	0,0541	0,1904	0,2932	0,258	0,1419	0,05	0,011	0,0013	0,0001

Полигон (многоугольник) распределения вероятностей дискретной случайной величины Xпредставлен на рис.:

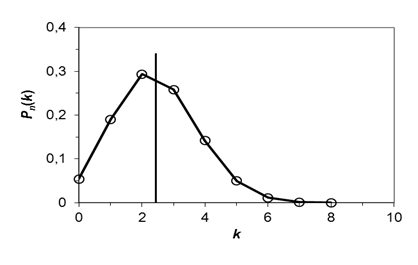
Рис. Полигон распределения вероятностей д.с.в. X=k.
Вертикальной линией показано математическое ожидание распределения M(X).

Найдем числовые характеристики распределения вероятностей д.с.в. X. Мода распределения равна 2 (здесь P8(2) = 0,2932 максимально). Математическое ожидание по определению равно:
M(X) = 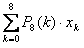= 2,4444,
где xk = k – значение, принимаемое д.с.в. X. Дисперсию D(X) распределения найдем по формуле:
D(X) = 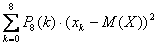= 4,8097.
Среднее квадратическое отклонение (СКО):
s(X) = 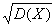= 2,1931.

Пример2
Дискретная случайная величинаX задана законом распределения

X
Р	0,3	0,1	0,6

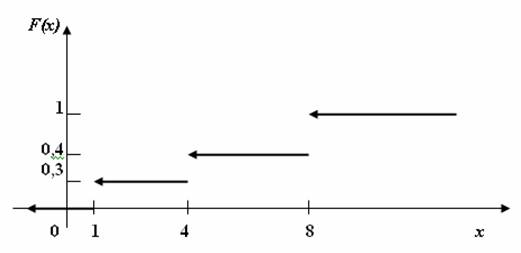
Найти функцию распределения F(x) и построить ее график.

Решение. Если 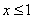, то 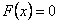(третье свойство).
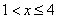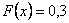Если , то . Действительно, X может принять значение 1 с вероятностью 0,3.
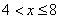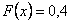Если , то . Действительно, если 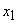удовлетворяет неравенству
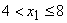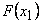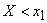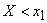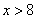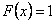, то равно вероятности события , которое может быть осуществлено, когда X примет значение 1 (вероятность этого события равна 0,3) или значение 4 (вероятность этого события равна 0,1). Поскольку эти два события несовместны, то по теореме сложения вероятность события равна сумме вероятностей 0,3 + 0,1=0,4. Если , то . Действительно, событие 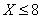достоверно, следовательно, его вероятность равна единице. Итак, функция распределения аналитически может быть записана так:

График этой функции:

Пример3
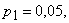
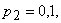
В магазине куплено 3 электроприбора: чайник, утюг и пылесос. Вероятность выхода из строя в течение гарантийного срока для каждого из них соответственно равны 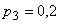. Составить закон распределения случайной величины X – числа приборов, вышедших из строя в течение гарантийного срока.

Решение. X – число приборов, вышедших из строя, имеет следующие возможные значения:
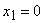- все три прибора не выйдут из строя в течении гарантийного срока;
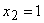- один прибор выйдет из строя;
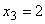- два прибора выйдут из строя;
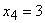- три прибора выйдут из строя.
Найдем соответствующие этим значениям вероятности. По условию, вероятности выхода из строя приборов равны: 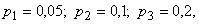тогда вероятности того, что приборы будут рабочими в течение гарантийного срока равны:


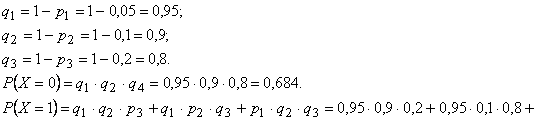
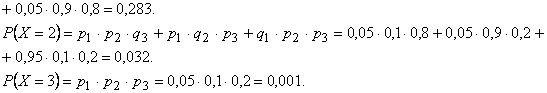
Закон распределения имеет вид:

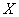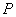	0,684	0,283	0,032	0,001

Проверка: 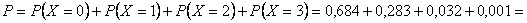1.