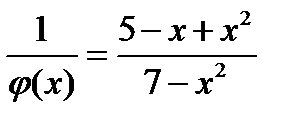Переменные и постоянные величины
Задача2.1
Период малых колебаний 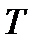 математического маятника вычисляется по формуле
математического маятника вычисляется по формуле 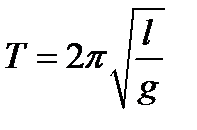 , где
, где 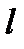 — длинна маятника,
— длинна маятника, 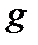 —ускорение силы тяжести.
—ускорение силы тяжести.
Какие из величин, входящих в эту формулу, являются абсолютными постоянными, параметрами, переменными?
Ответ.2 и 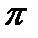 —абсолютные постоянные;
—абсолютные постоянные; 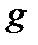 —параметр; значение этой величины постоянно только в данной точке земной поверхности, но изменяется при переходе от одной точки земной поверхности к другой;
—параметр; значение этой величины постоянно только в данной точке земной поверхности, но изменяется при переходе от одной точки земной поверхности к другой; 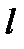 и
и 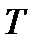 —величины переменные.
—величины переменные.
Задача2.2
Согласно закону Бойля—Мариотта, в изотермическом процессе 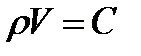 , где
, где 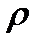 —давление газа, а
—давление газа, а 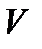 —занимаемый им объем. Указать в этой формуле переменные величины и параметр.
—занимаемый им объем. Указать в этой формуле переменные величины и параметр.
Ответ.Величины 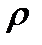 и
и 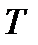 —переменные; величина
—переменные; величина 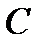 —параметр, так как она сохраняет постоянное значение только для данного газа и для данной температуры.
—параметр, так как она сохраняет постоянное значение только для данного газа и для данной температуры.
Задача2.3
В случае свободного падения тела в пустоте пройденный им путь 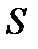 вычисляется по формуле
вычисляется по формуле 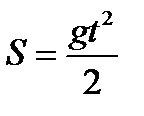 .
.
Какие из входящих в эту формулу величин являются постоянными, параметрами, переменными?
Ответ. 2 является абсолютной постоянной величиной (следует помнить, что все числа – абсолютные постоянные величины); 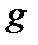 -параметр (см.задачу №2.1);
-параметр (см.задачу №2.1); 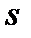 и
и 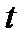 -переменные величины.
-переменные величины.
Задача2.4
Объем усеченного конуса вычисляется по формуле 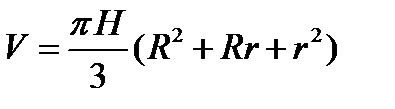 .
.
Указать, какие из величин, входящих в эту формулу ,являются переменными, абсолютными постоянными, параметрами.
Ответ. Величины 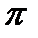 и 3 –абсолютные постоянные;
и 3 –абсолютные постоянные; 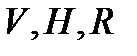 и
и 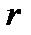 -переменные величины.
-переменные величины.
Ни одна из величин, входящих в эту формулу, не является параметром.
Определение частных значений функции
Для того чтобы найти частное значение функции по заданному частному значению аргумента, надо в аналогическое выражение функции поставить вместо аргумента его частное значение.
Задача2.5
Дана целая рациональная функция 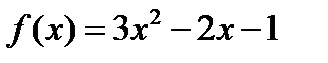 .
.
Вычислить: 1) 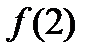 ;2)
;2) 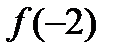 ;3)
;3) 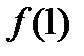 ;4)
;4) 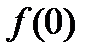 ;5)
;5) 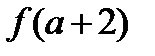 ;6)
;6) 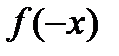 .
.
Решение.
1) 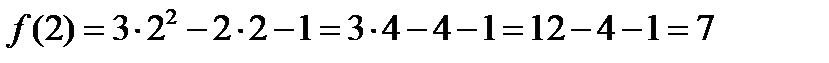 .
.
2) 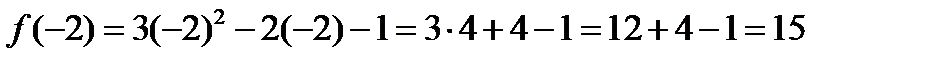 .
.
3) 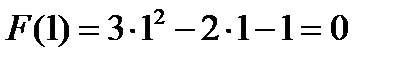 .
.
4) 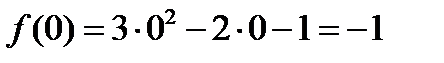 .
.
5) 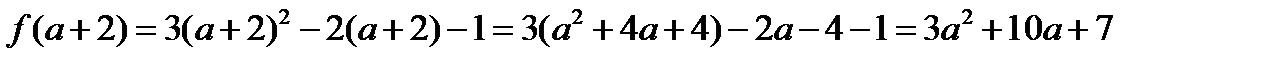 .
.
6) 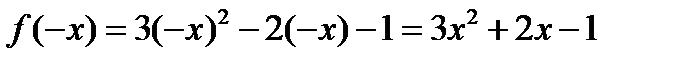 .
.
Задача2.6
(для самостоятельного решения). Дана целая рациональная функция 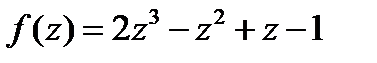 .
.
Вычислить:1) 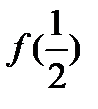 ;2)
;2) 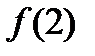 ;3)
;3) 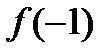 ;4)
;4) 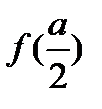 ;5)
;5) 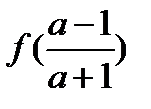 .
.
Ответ.
1) 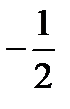 ;
;
2) 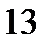 ;
;
3) 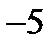 ;
;
4) 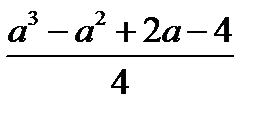 ;
;
5) 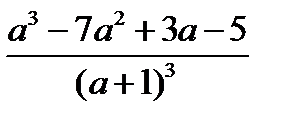 .
.
Задача2.7
Дана дробная рациональная функция 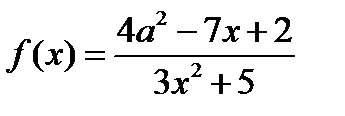 .
.
Вычислить:1) 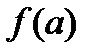 ;2)
;2) 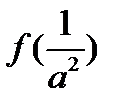 ;3)
;3) 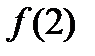 ;4)
;4) 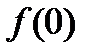 .
.
Решение.
1) 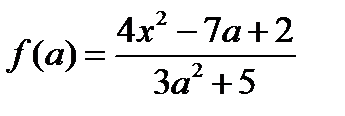 ;
;
2) 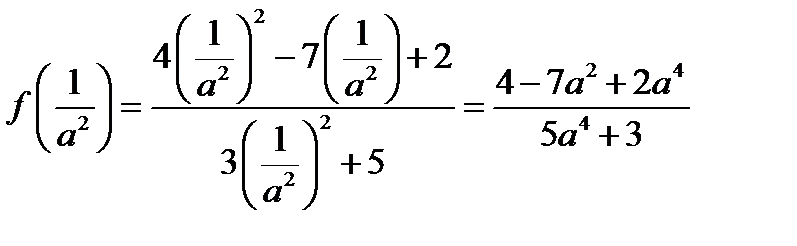 ;
;
3) 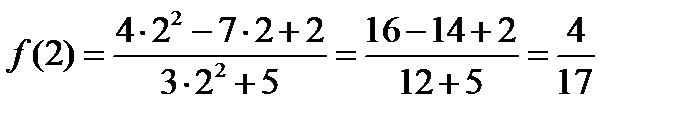 ;
;
4) 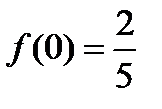 .
.
Задача2.8
(для самостоятельного решения). Дана функция 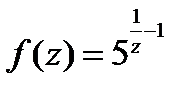 .
.
Вычислить:1) 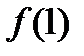 ;2)
;2) 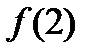 ;3)
;3) 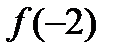 ;4)
;4) 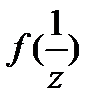 .
.
Ответ.
1) 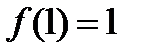 ;
;
2) 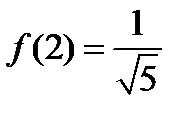 ;
;
3) 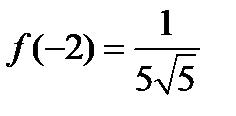 ;
;
4) 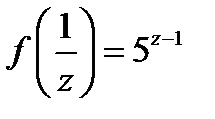 .
.
Задача2.9
Дана дробно—линейная функция 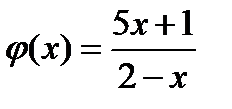 .
.
Найти:1) 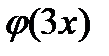 ;2)
;2) 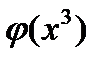 ;3)
;3) 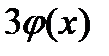 ;4)
;4) 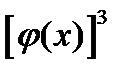 .
.
Решение.
1) Чтобы найти 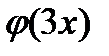 следует в выражении для
следует в выражении для 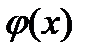 заменить
заменить 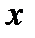 на
на 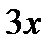 . Получаем
. Получаем 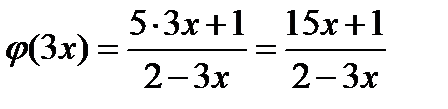 .
.
2) Заменяем в выражении 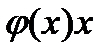 на
на 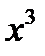 , получим
, получим 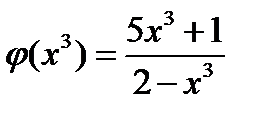 .
.
3) Следует отличать 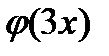 от
от 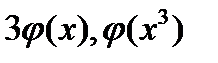 от
от 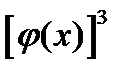 . Было найдено в
. Было найдено в
1), что 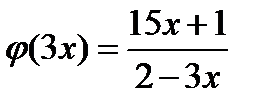 , а
, а 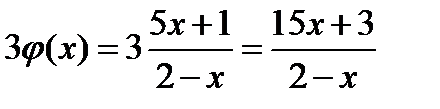 .
.
4) 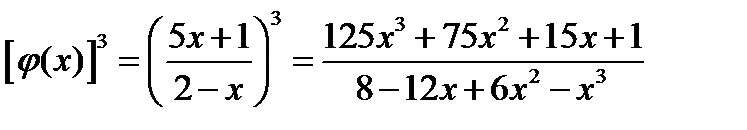
Задача2.10
(для самостоятельного решения).Дана функция 
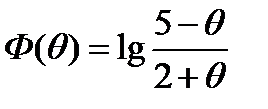 .
.
Найти:1) 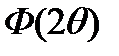 ;2)
;2) 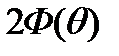 ;3)
;3) 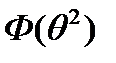 ;4)
;4) 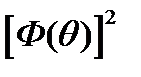 .
.
Ответ.
1) 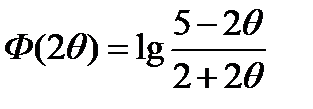 ;
;
2) 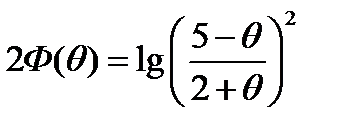 ;
;
3) 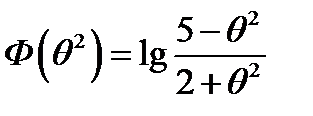 ;
;
4) 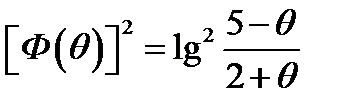 .
.
Задача2.11
(для самостоятельного решения). 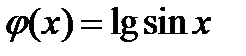 .Доказать, что
.Доказать, что 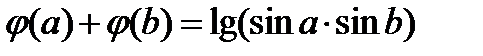
Задача2.12
(для самостоятельного решения). 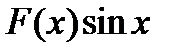 .Доказать, что
.Доказать, что 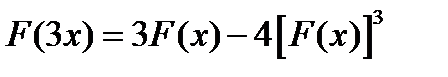 .
.
Задача2.13
Доказать, что если 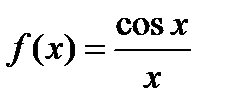 ,то
,то 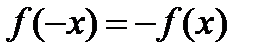 .
.
Решение.
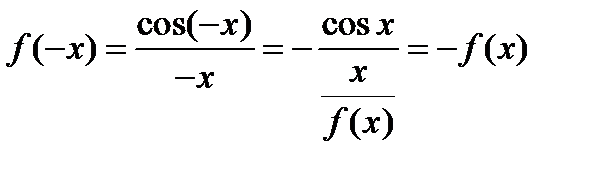 .
.
Задача2.14
(для самостоятельного контроля). 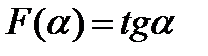 .Доказать, что
.Доказать, что 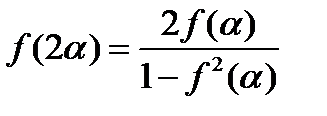 .
.
Задача2.15
(для самостоятельного решения).Доказать, что если 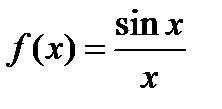 ,то
,то 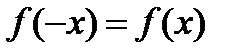 .
.
Задача2.16
Вычислить 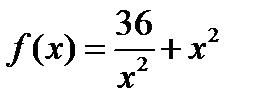 в точках, где
в точках, где 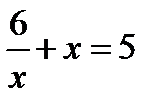 .
.
Решение.
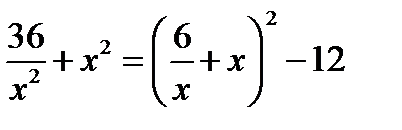 , а так как по условию
, а так как по условию 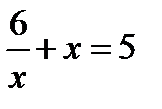 , то
, то 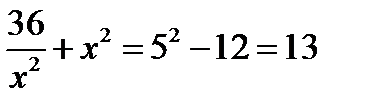 .
.
Задача2.17
Дано, что 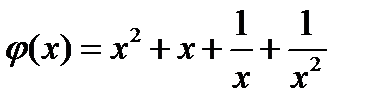 . Доказать что
. Доказать что 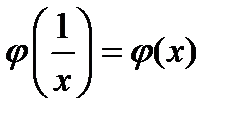 .
.
Решение.
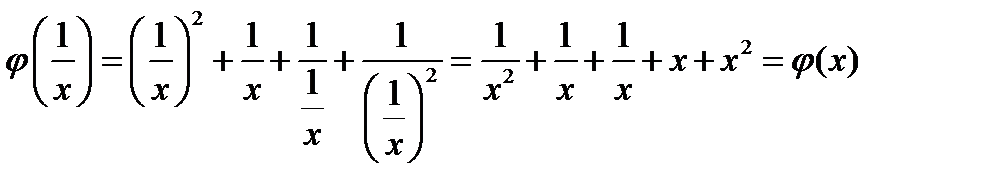 .
.
Задача 2.18
(для самостоятельного решения). Дана функция 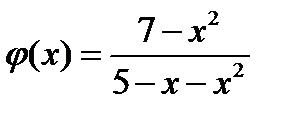 . Вычислить
. Вычислить 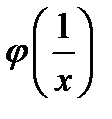 и
и 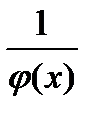 .
.
Ответ.
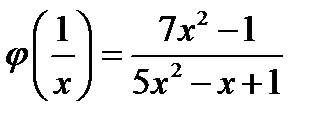 ;
;