Анализ полученных производственных функций

Исходные данные

№п/п	Объем производства (Y)	Затраты ОПФ (К)	Ресурсы трудозатрат (L)
	32,1	0,43	3,45
		0,77	3,48
	32,4	1,35	3,06
	33,2	1,99	3,66
	31,2	0,88	3,79
	34,8	0,98	3,85
	35,4	1,56	3,44
		2,09	4,08
	34,8	1,44	4,5
	33,3	2,13	4,31
	36,1	1,17	3,57
	38,3	1,44	3,55
	30,6	1,87	4,61
	32,1	2,66	3,99
	37,6	2,05	4,78

Результирующий показатель:

- объем производства (Y)

Факторные показатели:

- Затраты основных производственных фондов (К)

- Ресурсы трудозатрат (L)

Построение линейной и степенной формы производственной функции

Линейная модель:

Y = b₁K + b₂L

Y= -1,4*K+9,14*L

Степенная модель:

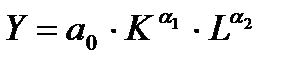
a₀=e^3,5184= 33,733

Y=33,73*K^0,03*L^(-0,009)

Анализ полученных производственных функций

Линейная:

Регрессионная статистика
Множественный R	0,991214
R-квадрат	0,982506
Нормированный R-квадрат	0,904237
Стандартная ошибка	4,802705
Наблюдения

Степенная:

Регрессионная статистика
Множественный R	0,203085
R-квадрат	0,041244
Нормированный R-квадрат	-0,11855
Стандартная ошибка	0,07309
Наблюдения

1.Множественный коэффициент корреляции в линейной модели равен 0,9912, что свидетельствует об очень тесной связи между факторами «Затраты ОПФ», «Ресурсы трудозатрат» и результирующим фактором «Объем производства».

Множественный коэффициент корреляции в степенной форме равен 0,2031, что также свидетельствует о слабой связи между факторами «Затраты ОПФ», «Ресурсы трудозатрат» и результирующим фактором «Объем производства».

2.Для проверки общего качества уравнения регрессии используется коэффициент детерминации R². R² у линейной модели равен 0,9825, это значит, что 98,25% дисперсии объема производства формируются в результате влияния затрат ОПФ и ресурсов трудозатрат, 1,75% дисперсии объема производства формируется под влиянием неучтенных в модели факторов. В этом случае R² почти равен единице, что говорит об очень высокой степени адекватности уравнения в целом.

Коэффициент детерминации у степенной модели равен 0,04. Это означает, что 4% дисперсии объема производства формируются в результате влияния затрат ОПФ и ресурсов трудозатрат, 96% дисперсии объема производства формируется под влиянием неучтенных в модели факторов. Значит, качество модели не столь хорошее, по сравнению с линейной моделью.

3. F-статистика анализирует статистическую значимость модели в целом.

Линейная модель в целом значима, о чем свидетельствуют показатели F – статистики: р<a на всех уровнях значимости ( т.е 0,0000 < 0,01;0,05;0,1).

Показатели F – статистики для степенной модели: р>a на всех уровнях значимости (т.е 0,7767 > 0,01;0,05;0,1), что также свидетельствует о статистической незначимости уравнения.

Следовательно, степенная модель плохо отражает связь между факторами и результатом, а линейная модель адекватно отражает связь между факторами и результатом.

4. Оценка параметров регрессии с помощью t-критерия Стьюдента. На основе t-статистики проверяется статистическая значимость каждого параметра в модели.

Для линейной модели:

По результатам t-теста можно сделать вывод, что коэффициент b1 незначим на всех уровнях значимости (т.е. р>a 0,565 > 0,01; 0,05;0,1), коэффициент b2 статистически незначим на всех уровнях значимости (р>a на всех уровнях значимости т.е 4,9 > 0,01;0,05;0,1).

Для степенной модели:

По результатам t-теста можно сделать вывод, что коэффициенты a, b1 и b2 статистически незначимы на всех уровнях значимости (т.к. р>a на всех уровнях значимости, т.е для а: 3,565>0,01;0,05;0,1; для b1 0,529>0,01;0,05;0,1; для b2: 0,96> 0,01;0,05;0,1)

Согласно анализу по полученным результатам следует отдать предпочтение линейной модели регрессии, которая имеет вид:

Y= -1,4*K+9,14*L