Часть iii. электричество и магнетизм

ЭЛЕКТРОСТАТИКА

Тема 1. Теорема Остроградского-Гаусса для электростатического поля

Электростатическое поле – это особый вид материи, с помощью которой происходит взаимодействие заряженных тел.

Точечным называется заряд, сосредоточенный на теле, размерами которого можно пренебречь по сравнению с расстоянием до других заряженных тел, с которыми он взаимодействует.

Закон Кулона:сила взаимодействия F между двумя неподвижными точечными зарядами q₁ и q₂ прямопропорциональна величинам этих зарядов и обратно пропорциональна квадрату расстояния r между ними:

,

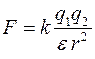где 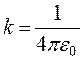(e₀ – электрическая постоянная);

e – диэлектрическая проницаемость среды, показывающая во сколько раз сила взаимодействия зарядов в данной среде меньше, чем в вакууме.

Кулоновская сила 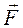направлена по прямой, соединяющей взаимодействующие точечные заряды, соответствует притяжению в случае разноименных зарядов и отталкиванию в случае одноименных зарядов. Элект­рические поля, которые создаются неподвижными электрическими зарядами, называ­ются электростатическими.

Для обнаружения и опытного исследования электростатического поля можно использовать пробный точечный заряд q₀ . Если этот заряд поместить в какую- либо точкуэлектростатического поля,то на него будетдействовать сила 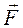, величина и направление которой определяет силовую характеристику электростатического поля, носящую названиенапряженности электростатического поля.

Напряженность электростатического поля в данной точке есть физическая величина , определяемая силой, действующей на пробный точечный положительный заряд q₀ , помещенный в эту точку поля, то есть:

.

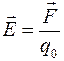Напряжённость электростатического поля, создаваемого точечным зарядом q в любой точке поля, находящейся на расстоянии r от этого заряда:

.

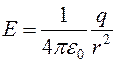Электростатическое поле может быть изображено графически с помощьюсиловых линий.Силовая линия — это такая линия, касательная в каждой точке к которой совпадает по направлению с вектором напряженности электростатическго поля в данной точке (рис. 1, 2).

Рис. 1 Рис. 2

Если поле создается точечным зарядом, то силовые линии – это радиальные прямые, выходящие из положительного заряда (рис. 2, а), и входя­щие в отрицательный заряд (рис. 2, б).

С помощью силовых линий можно характеризовать не только направление, но и величину напряженности электростатического поля, связывая её с густотой силовых линий. Большей густоте силовых линий соответствует большая величина напряженности (рис. 1, 2). Количественно числу силовых линий, прони­зывающих единичную площадку, расположенную перпендикулярно силовым линиям, ставится в соответствие величина напряженности электростатического поля. В этом случае определенному заряду q, создающему поле, соответствует определенное число N силовых линий, выходящих (для 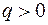) из заряда или входящих (для 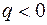) в заряд, а именно: .

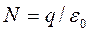Поток вектора напряженности электростатического поля через произвольную площадку S характеризуется числом силовых линий, пронизывающих данную площадку S.

Если площадка S перпендикулярна силовым линиям (рис. 3), то поток Ф_Е вектора напряженности через данную площадку S : .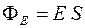

Рис. 3 Рис. 4

Рис. 3

Если же площадка S расположена неперпендикулярно силовым линиям электро-статического поля (рис. 4), то поток вектора через данную площадку S :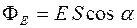

,

где α – угол между векторами напряженности и нормали 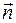к площадке S.

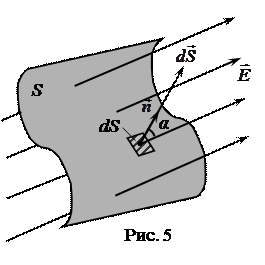Для того, чтобы найти поток Ф_Е вектора напряженности через произвольную поверхность S, необходиморазбить эту поверхность на элементарные площадки dS (рис. 5),определить элементарный поток dФ_Е через каждую элементарную площадку dS по формуле: ,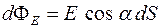

а затем все эти элементарные потоки dФ_Е сложить, что приводит к интегрированию:

,

Рис. 7

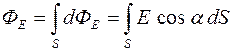где α – угол между векторами напряженности и нормали 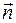к данной элементарной площадке dS .

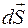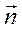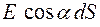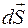Если ввести вектор (рис. 5) как вектор, равный по величине площади площадки dS и направленный по вектору нормали к площадке dS , то величина , где a – угол между векторами и может быть записана в виде скалярного произведения векторов и 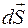, то есть, как 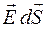, а полученное соотношение для потока вектора примет вид:

.

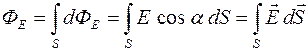Теорема Остроградского - Гаусса для электростатического поля. Теорема Остроградского - Гаусса для электростатического поля связывает между собой величину потока Ф_Е вектора напряженности электростатического поля в вакууме через произвольную замкнутую поверхность S с величинойзаряда q, заключенного внутри данной замкнутой поверхности S (рис. 6).

Рис. 6

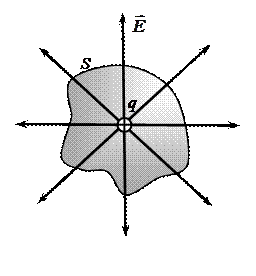Поскольку все силовые линии, выходящие из заряда (для 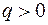) или входящие в заряд (для 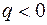), пронизываютпроизвольную замкнутую поверхность S, охватывающую этот заряд (рис. 6), то величина потока Ф_Е вектора напряженности электростатического поля через эту произвольную замкнутую поверхность S будет определяться числом N силовых линий, выходящих из заряда (для 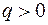) или входящих в заряд (для ):

.

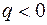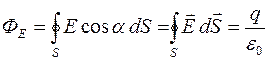Это соотношение есть теорема Остроградского-Гауссадляэлектростатического поля.

Таккак поток считается положитель­ным, если силовые линии выходят из поверхности S, и отрицательным для линий, входящих в поверхность S, то в случае, если внутри произвольной замкнутой поверхности S находится не один, а несколько (n) разноименных зарялов, то теорема Остроградского - Гаусса для электростатического поля формулируется следующим образом:

поток вектора напряженности электростатического поля в вакууме через произ­вольную замкнутую поверхность равен алгебраической сумме заключенных внутри этой поверхности зарядов, деленной на e₀:

.

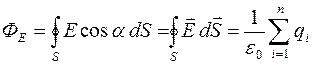В общем случае электрические заряды могут быть распределены внутри объёма, ограниченного замкнутой поверхностью S, с некоторой объемной плотностью 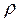( 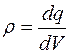), различной в разных местах пространства. Тогда суммарный заряд, заключенный внутри этой замкнутой поверхности S, охватывающей объем V,равен: .

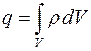В таком случае теорема Остроградского - Гаусса приобретает вид:

.

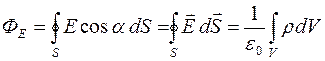Напряженность электростатического поля зависит от диэлектрических свойств среды. В диэлектрике напряженность поля меньше, чем напряженностьвнешнего электростатического поля в вакууме, в котором находится диэлектрик, в e раз (e – диэлектрическая проницаемость среды), а модуль вектора , переходя через границу диэлектриков, скачко­образно изменяется. Поэтому для характеристики электростатического поля, кроме вектора напряженности , введен векторэлектрического смещения 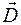, модуль которого не изменяется при переходе из одной диэлектрической среды в другую.

Вектор электрического смещения 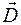по определению: .

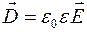Используя то, что в вакууме 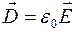, теорема Остроградского-Гаусса для электростатического поля может быть переформулирована следующим образом:

,

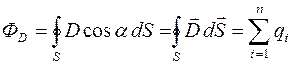то есть поток вектора смещения 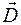электростатического поля через произ­вольную замкнутую поверхность S равен алгебраической сумме заключенных внутри этой поверхности зарядов.

В случае, если электрические заряды распределены внутри объёма V, ограни-ченного замкнутой поверхностью S, с некоторой объемной плотностью 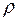, теорема Остроградского-Гаусса для электростатическогополяможет быть переформулирована сдедующим образом:

.

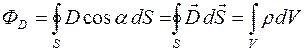Тема 2. Работа сил электростатического поля. Потенциал

Если в электростатическом поле, создаваемом точечным зарядом q, перемещается другой пробный заряд q₀из точки 1 в точку 2 вдоль произвольной траектории (рис. 7), то при этом совершается работа сил электростатического поля.

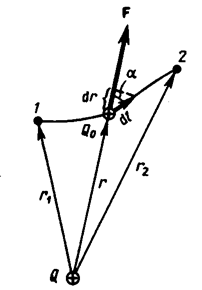Элементарная работа dA силы 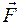на элементарном перемещении равна:

.

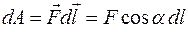Из рисунка 7 видно, что .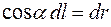

Тогда ( ).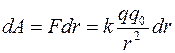

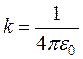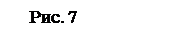Работа А при перемещении заряда q₀ вдоль траектории от точки 1 до точки 2:

,

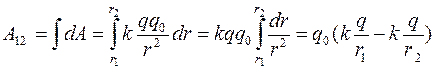то есть работа при перемещении заряда из точки 1 в точку 2 в электростатическом поле не зависит от траектории перемещения, а определяется только положениями начальной (1) и конечной (2) точек, то есть электростатическое полеточечного заряда является потенциальным.

Работа, совершаемая силами электростатического поля при перемещении заряда q₀из точки 1 в точку 2, выражается следующим образом:

,

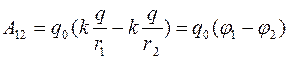где φ₁ и φ₂ – потенциалы электростатического поля в точках 1 и 2.

Потенциал электростатического поля определяется с точностью до произвольной аддитивной постоянной С, то есть для поля точечного заряда q:

.

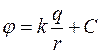Тогда , .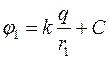

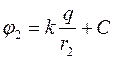Разность потенциалов двух точек 1 и 2 в электростатическом поле определяется работой 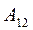, совершаемой силами поля, при перемещении пробного точечного поло­жительного заряда q₀из точки 1 в точку 2 :

.

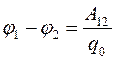Если считать, что при удалении на бесконечность потенци­ал электростатического поля обращается в нуль (φ_∞=0), то потенциал φ₁ в данной точке поля можно определить следующим образом:

,

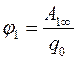то есть потенциал j в данной точке поля равен работе сил электростатического поля при перемещении точечного поло­жительного единичного заряда из данной точки поляна бесконечность.

Циркуляцией вектора напряженности электростатического поля по произвольному замкнутому контуру L называется интеграл

.

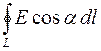Для того, чтобы найти циркуляцию вектора напряженности по произвольному замкнутому контуру L, необходимо выбрать направление обхода контура, разбить этот контур L на элементы , для каждого элемента рассчитать величину 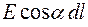(a – угол между векторами и ), а затем все эти величины сложить, что приводит к искомому интегралу.

Однако для электростатического поля циркуляция вектора напряженности по произвольному замкнутому контуру L может быть легко получена из формулы работы, совершаемой силами электростатического поля при перемещении пробного заряда q₀по произвольному замкнутому контуру L.

С одной стороны, эта работа равна:

,

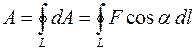а с учетом того, что 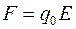эта работа равна:

.

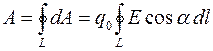С другой стороны, эта работа может быть определена с помощью формулы:

,

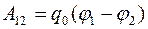из которой следует, что для произвольного замкнутого контура эта работа равна нулю, так как 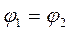. Тогда и циркуляция вектора по произвольному замкнутому контуру L тоже равна нулю, то есть:

.

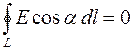Величина 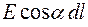, где a – угол между векторами и может быть записана в виде скалярного произведения векторов и , то есть, как 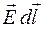, а полученное соотношение для циркуляции вектора примет вид:

.

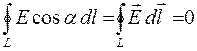Полученное соотношение является признаком потенциальногосилового поля. Обращение в нуль циркуляции вектора означает, что силовые линии электростатического поля не являются замкнутыми, они начинаются и заканчиваются на зарядах (соответственно на положительных или отрицательных) или же уходят в бесконечность, что также является свойством потенциальногосилового поля.

Связь между напряженностью и потенциалом электростатического поля

Напряженность и потенциал φ электростатического поля связаны между собой следующим образом:

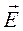= – grad φ или 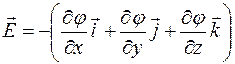, где

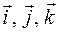– единичные векторы координатных осей Ох, Оy, Оz, соответственно.

Знак минус в приведенной формуле означает, что вектор напряженности электростатического поля направлен в сторону максимального убывания потенциала j .

Для графического изображения распределения потенциала электростатического поля используютсяэквипотенциальные поверхности,то естьповерхности, во всех точках которых потенциал j имеет одно и то же значение.

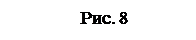
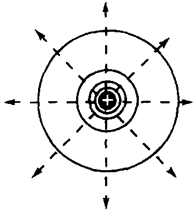Например, для поля, созданного точечным зарядом q, потенциал j определяется выражением: 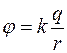, а эквипотенциальными поверхностями являются кон­центрические сферы (рис. 8). Из этого рисунка видно, что в случае точечного заряда силовые линии поля (штриховые линии) нормальны к эквипотенциальным поверхностям.

Это свойство нормального взаимного расположения силовых линий и эквипотенциальных поверхностей поля является общим для любых случаев электростатического поля. То есть, зная расположение силовый линий электростатического поля, можно построить эквипотенциальные поверхности и, наоборот, по известному расположению эквипотенциальных поверхностей можно построить силовые линии электростатического поля.

Магнитное поле

Тема 3. Магнитное поле. Закон Био-Савара-Лапласа

Электрический ток создает поле, действующее на магнитную стрелку. Стрелка ориентируется по касательной к окружности, лежащей в плоскости, перпендикуляной к проводнику с током (рис. 9).

Основной характеристикой магнитного поля является вектор индукция . Принято, что вектор индукция магнитного поля направлен в сторону север-ного полюса магнитной стрелки, помещенной в данную точку поля (рис. 9).

По аналогии с электрическим полем, магнитное поле также может быть изображено графически с помощью силовых линий (линий индукции магнитного поля).

Силовая линия – это такая линия, касательная к которой в каждой точке совпадает по направлению с вектором индукции магнитного поля. Силовые линии магнитного поля, в отличие от силовых линий электростатического поля, являются замкнутыми и охватывают проводники с током. Направление силовых линий задается правилом правого винта (правилом буравчика): головка винта, ввинчиваемого по направлению тока, враща­ется в направлении линий магнитной индукции (рис. 9).

Рис. 9

Для нескольких источников магнитного поля согласно принципу суперпозиции магнитных полей индукция результирующего магнитного поля равна векторной сумме индукций всех отдельных магнитных полей:

.

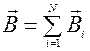Вектор индукции магнитного поля, создаваемого проводником с током 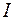, можно определить с помощью закона Био-Савара-Лапласа.При этомнеобходимо учесть то, что закон Био-Савара-Лапласапозволяет найти модуль и направление лишьвектора индукции 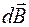магнитного поля, создаваемого элементом проводника с током 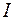. Поэтому, для определения вектора индукции магнитного поля, создаваемого проводником с током 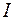, необходимо первоначально разбить этот проводник на элементы проводника , для каждого элемента с помощью закона Био-Савара-Лапласа найти вектор индукции 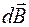, а затем, используя принцип суперпозиции магнитных полей, сложить векторно все найденные вектора индукции .

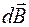Закон Био-Савара-Лапласав векторной форме:

,

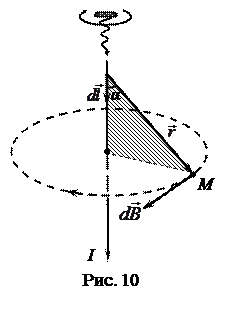
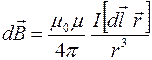где 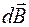– индукция магнитного поля в точке M, заданной радиусом-вектором 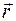, проведенным от начала вектора до этой точки;

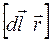– векторное произведение векторов и ;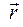

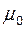– магнитная постоянная,

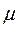– магнитная проницаемость среды.

Направление вектора 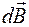определяется по правилу правого винта: направление враще­ния головки винта дает направление вектора 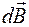, если поступательное движение винта совпадает с направлением тока в элементе проводника (рис. 10).

В скалярном виде закон Био-Савара-Лапласа:

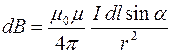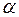, где – угол между векторами и .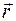

Магнитное поле линейного тока.Для нахождения индукции магнитного поля, созданного прямым проводником с током (рис. 11), необходимо разбить весь проводник на элементы , для каждого элемента проводника с током I найти вектор индукции 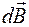, а затем векторно сложить все найденные .

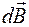В произвольной точке М, удаленной от оси проводника на расстояние b (рис. 11), векторы 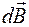от всех элементов проводника с током I имеют одинаковое направление, перпендикулярное плоскости чертежа («к нам»). Поэтому сложение векторов 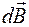можно заменить сложением их модулей.

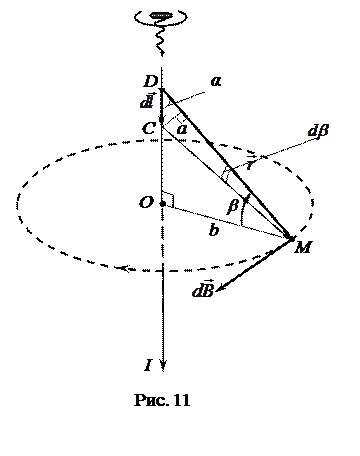
По закону Био-Савара-Лапласа модуль вектора магнитной индукции 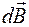в точке М поля, созданного элементом проводника с током I :

.

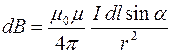В качестве переменной интегрирования выберем угол 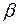, выразив через этот угол все остальные величины.

Из рисунка 11 следует, что 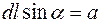, а с другой стороны, .

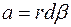Тогда 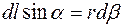, а модуль вектора магнитной индукции 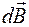в точке М :

.

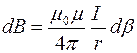Из прямоугольного треугольника DOM :

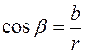, откуда .

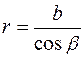Следовательно, индукция dB, создаваемая элементом проводника dl с током I :

.

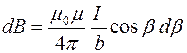Теперь можно перейти к интегрированию:

.

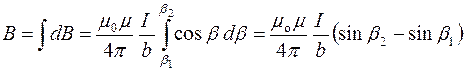Так как угол 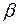для прямого тока изменяется в пределах от 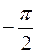до 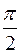, то магнитная индукция поля прямого тока:

.

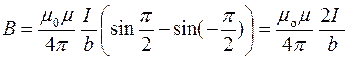Следовательно,

.

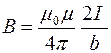Магнитное поле в центре кругового проводника с током. Для нахождения индукции магнитного поля в центре кругового проводника с током необходимо разбить этот проводник на элементы , причем все элементы проводника с током создают в центре кругового тока магнитные поля одинакового направления – вдоль нормали к плоскости витка (рис. 12). 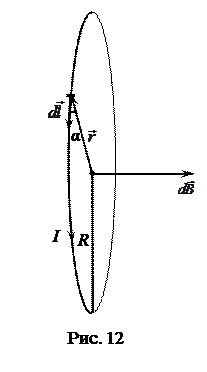Поэтому сложение век­торов 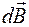можно заменить сложением их модулей dB.

По закону Био-Савара-Лапласа модуль вектора :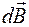

.

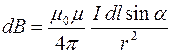Так как все элементы проводника перпендикулярны соответствующим радиусам-векторам 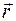(рис. 12), то sina = 1 для всех элементов . Расстояния r для всех элементов проводника также одинаковые (r = R).

Тогда выражение для модуля вектора 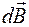примет вид:

.

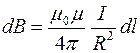Теперь для нахождения модуля вектора 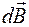можно перейти к интегрированию:

.

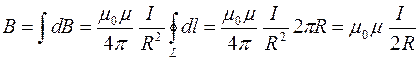Следовательно, индукция магнитного поля B в центре кругового проводника радиусом R с током I :

.

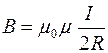Тема 4. Действие магнитного поля на проводник с током (закон Ампера) и на движущийся заряд (сила Лоренца)

Закон Ампера. На элемент проводника с током I , помещённый в магнитное поле с индукцией действует сила 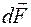( 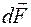– сила Ампера): .

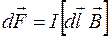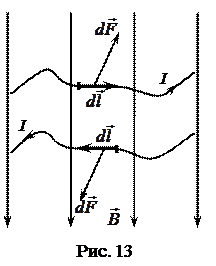Модуль вектора : ,

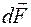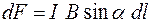где 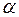– угол между векторами и .

Направление вектора 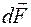можно определить по правилу левой руки: если силовые линии входят в ладонь, а четыре вытянутых пальца располагаются по току, то отведённый большой палец укажет направление силы Ампера(рис. 13, сила 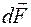перпендикулярна плоскости рисунка).

Сила Лоренца. На заряд q , движущийся со скоростью 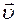в магнитном поле с индукцией , действует сила 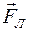( 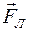– сила Лоренца ): .

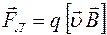Модуль вектора : ,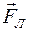

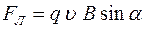где α – угол между векторами 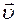и .

Направление вектора 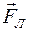может быть определено по правилу левой руки для движущихся положительных зарядов и по правилу правой руки для движущихся отрицательных зарядов: если силовые линии магнитного поля входят в ладонь, а четыре вытянутых пальца располагаются по скорости движения частицы, то отведённый большой палец укажет направление силы Лоренца (рис.14, сила 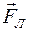перпендикулярна плоскости рисунка).

Тема. 5. Магнитный поток. Теорема Гаусса для магнитного поля

Поток вектора магнитной индукции 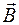(илимагнитный поток) через произвольную площадку S характеризуется числом силовых линий магнитного поля, пронизывающих данную площадку S. Если площадка S расположенаперпендикулярно силовым линиям магнитного поля (рис. 15), то поток Ф_B

вектора индукции через данную площадку S : .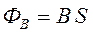

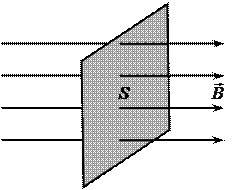
Рис. 15 Рис. 16

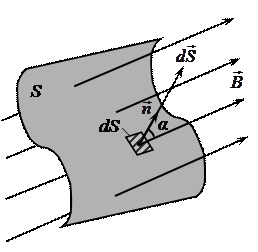
Если площадка S расположена неперпендикулярно силовым линиям магнитного поля (рис. 16), то поток Ф_B вектора индукции через данную площадку S :

,

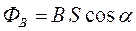где α – угол между векторами и нормали 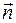к площадке S.

Рис. 17

Для того, чтобы найти поток Ф_B вектора магнитной индукции через произвольную поверхность S, необходиморазбить эту поверхность на элементарные площадки dS (рис. 17)иопределить элементарный поток 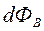вектора через каждую площадку dS по формуле: ,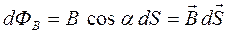

где α – угол между векторами и нормали 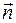к данной площадке dS;

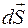– вектор, равный по величине площади площадки dS и направленный по вектору нормали 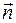к данной площадке dS .

Тогда поток вектора через произвольную поверхность S равен алгебраической сумме элементарных потоков 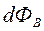через все элементарные площадки dS, на которые разбита поверхность S, что приводит к интегрированию:

.

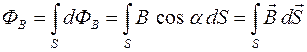Теорема Гаусса для магнитного поля

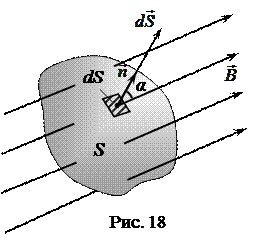Для произвольной замкнутой поверхности S (рис. 18) поток вектора индукции магнитного поля через эту поверхность S можно рассчитать по формуле:

.

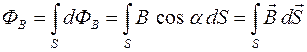С другой стороны, число линий магнитной индукции, входящих внутрь объема, ограниченного этой замкнутой поверхностью, равно числу линий, выходящих из этого объема (рис. 18). Поэтому, с учетом того, что поток вектора индукции магнитного поля считается положитель­ным, если силовые линии выходят из поверхности S, и отрицательным для линий, входящих в поверхность S, суммарный поток Ф_B вектора индукции через произвольную замкнутую поверхность S равен нулю, то есть:

,

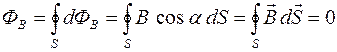что составляет формулировку теоремы Гаусса для магнитного поля.

Тема. 6. Явление электромагнитной индукции. Закон Фарадея

Явление возникновения электрического тока в замкнутом проводящем контуре в результате изменения магнитного потока, пронизывающего этот контур, называется явлением электромагнитной индукции. Возникновение индукционного электрического тока в контуре указывает на наличие в этом контуре электродвижущей силы, называемойэлектродвижущей силой (ЭДС) электро­магнитной индукции.

Согласно закону Фарадея, величина ЭДС электро­магнитной индукции 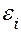определяется только скоростью изменения магнитного потока, пронизывающего проводящий контур, а именно:

величина ЭДС электро­магнитной индукции 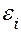прямо пропорциональна скорости изменения магнитного потока, пронизывающего проводящий контур:

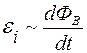(закон Фарадея).

Направление индукционного тока в контуре определяется по правилу Ленца: индукционный ток в контуре всегда имеет такое направление, что создаваемое этим током магнитное поле препятствует изменению магнитного потока, вызвавшему этот индукционный ток.

Закон Фарадея с учетом правила Ленца можно сформулировать следующим образом: величина ЭДС электро­магнитной индукции 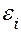в контуре численно равна и противоположна по знаку скорости изменения магнитного потока через поверхность, ограниченную этим контуром, то есть:

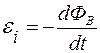(закон Фарадея с учетом правила Ленца).

Тема 7. Циркуляция вектора магнитной индукции

Циркуляцией вектора магнитной индукции по произвольному замкнутому контуру L называется интеграл:

.

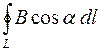Для того, чтобы найти циркуляцию вектора магнитной индукции по произвольному замкнутому контуру L, необходимо выбрать направление обхода контура, разбить этот контур L на элементы , для каждого элемента рассчитать величину 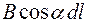(a – угол между векторами и ), а затем все эти величины сложить, что приводит к искомому интегралу.

Однако циркуляцию вектора по произвольному замкнутому контуру L можно рассчитать, используятеорему о циркуляции вектора .

Теорема о циркуляции вектора : циркуляция вектора по произвольному замкнутому контуру L равна произведению магнитной постоянной m₀ на алгебраическую сумму токов, охватываемых этим контуром L:

,

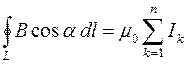где n – число проводников с токами, охватываемых контуром L. Положительным считается ток, направление которого образует с направлением обхода по контуру правовинтовую систему; ток противоположного направления считается отрицательным.

Величина 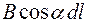, где a – угол между векторами и может быть записана в виде скалярного произведения векторов и , то есть, как 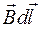, а полученное соотношение для циркуляции вектора примет вид:

.

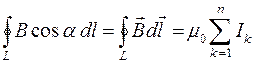Магнитное поле претерпевает изменения при переходе из одного вещества в другое, что определяется магнитными свойствами вещества, которые характеризуются величиной магнитной проницае­мости среды ( m ).

Кроме вектораиндукции магнитного поля, учитывающего магнитные свойства вещества, для описания магнитного поля введен также и векторнапряженности 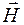магнитного поля, причем для однород­ной изотропной среды вектор магнитной индукции связан с вектором напряженности 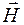магнитного поля следующим соотношением:

,

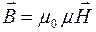где m₀ – магнитная постоянная, m – магнитная проницае­мость среды.

Поскольку для вакуума m = 1 , то с учетом приведенного соотношения может быть получена циркуляция вектора напряженности 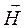по произвольному замкнутому контуру L в следующем виде:

,

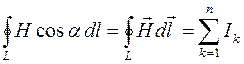то есть циркуляция вектора 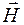по произвольному замкнутому контуру L равна алгебраической сумме токов, охватываемых этим контуром L.

Сравнивая векторные характеристики электростатического ( и ) и 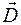магнитного ( и 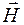) полей, следует отметить, что аналогом вектора напряженности электростатического поля является вектор магнитной индукции , так как векторы и определяют силовые действия этих полей и зависят от свойств среды, а аналогом вектора электрического смещения 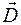является вектор напряженности 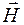магнитного поля.