Повторные независимые испытания

ЗАДАНИЕ 1

Задача 1. Вероятность стрелка попасть в цель при одном выстреле равна 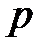. Найти вероятность того, что при 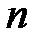выстрелах стрелок попадает в цель:

а) 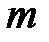раз;

б) не менее 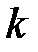раз.

№ варианта
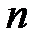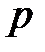	0,7	0,9	0,4	0,8	0,5	0,4	0,6	0,3	0,3	0,2

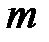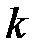Задача 2. На прием к врачу записались 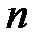человек. Вероятность того, что пациенту потребуется сдать кровь на анализ, равна 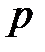. Найти вероятность того, что необходимо сдать кровь на анализ:

а) 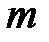пациентам;

б) не менее, чем 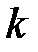пациентам.

№ варианта
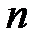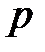	0,4	0,5	0,7	0,3	0,6	0,8	0,7	0,4	0,6	0,9

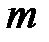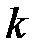Задача 3. Вероятность того, что телевизор потребует ремонта в течение 5 лет, равна 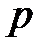. Найти вероятность того, что из 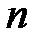купленных телевизор в течение 5 лет потребуют ремонта:

а) 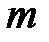телевизоров;

б) не менее 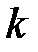телевизоров.

№ варианта
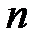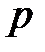	0,2	0,1	0,3	0,4	0,7	0,5	0,6	0,4	0,8	0,3

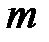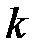ЗАДАНИЕ 2

Задача 1. Вероятность того, что завод выпускает телефонный аппарат высшего сорта, равна 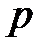. Предприятие приобретает 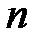телефонных аппаратов. Найти:

а) наивероятнейшее число телефонных аппаратов высшего сорта и вероятность того, что именно это число телефонных аппаратов высшего сорта приобретено предприятием;

б) вероятность того, что среди приобретенных телефонных аппаратов окажется 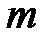аппаратов высшего сорта.

№ варианта
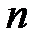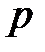	0,2	0,4	0,5	0,6	0,3	0,7	0,8	0,6	0,8	0,4

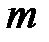Задача 2. В магазин в день заходят 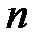человек. Вероятность того, что покупатель сделает покупку, равна 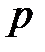. Найти:

а) наивероятнейшее число покупателей, которые сделают покупку, и вероятность того, что именно это количество человек сделают покупку;

б) вероятность того, что 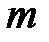человек сделают покупку.

№ варианта
	0,3	0,4	0,5	0,4	0,3	0,3	0,4	0,3	0,2	0,1

Задача 3. Всхожесть семян равна 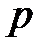. Посажено 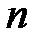семян. Найти:

а) наивероятнейшее число взошедших семян и вероятность того, что именно это количество семян взойдет;

б) вероятность того, что взойдет 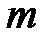семян.

№ варианта
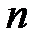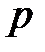	0,8	0,6	0,5	0,7	0,8	0,8	0,7	0,9	0,7	0,6

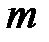ЗАДАНИЕ 3

Задача 1. В районе 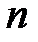предприятий, финансовую деятельность которых проверяет налоговая инспекция. Вероятность того, что по результатам проверки предприятию будут предъявлены штрафные санкции, равна 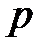Найти вероятность того, что штрафные санкции будут предъявлены:

а) не менее 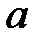и не более 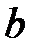предприятиям;

б) не менее 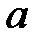предприятиям.

№ варианта
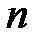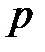	0,4	0,3	0,6	0,5	0,4	0,8	0,6	0,4	0,6	0,5

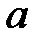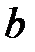Задача 2. Вероятность того, что абитуриент вуза, окончивший школу, станет студентом, равна 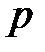. Найти вероятность того, что среди 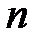абитуриентов вуза, окончивших школу, студентами станут:

а) не менее 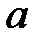и не более 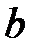человек;

б) не менее 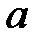человек.

№ варианта
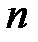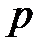	0,6	0,7	0,8	0,6	0,5	0,9	0,8	0,7	0,6	0,9

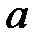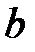Задача 3. Вероятность изготовления на станке детали первого сорта равна 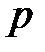. Изготовлено 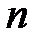деталей. Найти вероятность того, что деталей первого сорта будет изготовлено:

а) не менее 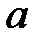и не более ;

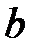б) не менее 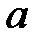штук.

№ варианта
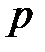	0,5	0,2	0,3	0,4	0,5	0,6	0,7	0,8	0,9	0,4

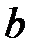ЗАДАНИЕ 4

Задача 1. За день обувной отдел магазина посещают 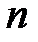человек. Вероятность того, что спрос покупателя будет удовлетворен, равна 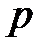. Найти вероятность того, что абсолютная величина отклонения доли покупателей, сделавших покупку, от вероятности 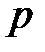не превысит .

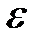№ варианта
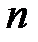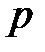	0,4	0,3	0,2	0,6	0,5	0,7	0,5	0,6	0,8	0,3
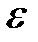	0,01	0,02	0,05	0,04	0,03	0,01	0,02	0,03	0,04	0,05

Задача 2. Вероятность того, что после вызова машина скорой помощи прибудет в течение 10 минут, равна 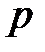. На станцию в течение дня поступило 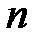вызовов. Найти вероятность того, что абсолютная величина отклонения доли машин, прибывших вовремя, от вероятности 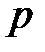не превысит .

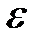№ варианта
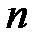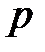	0,7	0,6	0,5	0,4	0,3	0,5	0,4	0,3	0,2	0,1
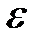	0,01	0,02	0,03	0,04	0,05	0,01	0,02	0,03	0,04	0,05

Задача 3. Сколько раз надо подбросить игральный кубик, что бы с вероятностью, равной 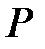, можно было утверждать, что абсолютная величина отклонения частности выпадения шести очков от вероятности выпадения шести очков в одном испытании не превысит ?

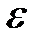№ варианта
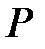	0,9545	0,95	0,9973	0,9426	0,6873	0,9426	0,9545	0,95	0,9973	0,6873
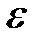	0,01	0,02	0,03	0,04	0,05	0,01	0,02	0,03	0,04	0,05

Рекомендуемая литература

1. Математика для экономических специальностей вузов. Ч. 2 / Под ред. Р.Ш. Марданова – Казань: Изд-во КФЭИ, 2001. - Гл.. 14, с. 29 – 42.

2. Сборник задач по математике для экономистов: учебное пособие под ред. проф. Р.Ш. Марданова. – Казань: Изд-во КГУ, 2009. - Гл.. 12, №№12.35 – 12.55.

Индивидуальная работа №4