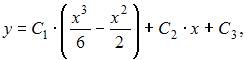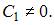Дифференциальные уравнения высших порядков, допускающие понижение порядка.
 ЗАДАНИЕ N 35 сообщить об ошибке
ЗАДАНИЕ N 35 сообщить об ошибке
Тема: Дифференциальные уравнения высших порядков, допускающие понижение порядка
Общее решение дифференциального уравнения 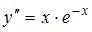 имеет вид …
имеет вид …
 | 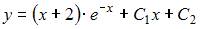 | ||
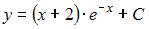 | |||
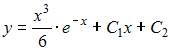 | |||
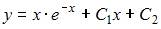 |
Решение:
Проинтегрируем последовательно обе части уравнения два раза: 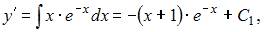
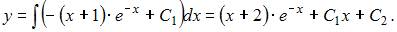
То есть общее решение имеет вид 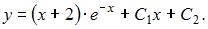
 ЗАДАНИЕ N 21 сообщить об ошибке
ЗАДАНИЕ N 21 сообщить об ошибке
Тема: Дифференциальные уравнения высших порядков, допускающие понижение порядка
Общее решение дифференциального уравнения 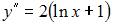 имеет вид …
имеет вид …
 | 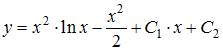 | ||
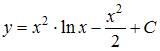 | |||
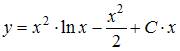 | |||
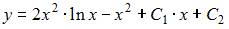 |
Решение:
Проинтегрируем последовательно обе части уравнения два раза: 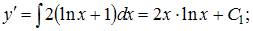
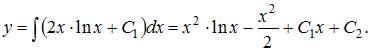
То есть общее решение примет вид 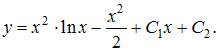
 ЗАДАНИЕ N 7 сообщить об ошибке
ЗАДАНИЕ N 7 сообщить об ошибке
Тема: Дифференциальные уравнения высших порядков, допускающие понижение порядка
Общее решение дифференциального уравнения 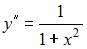 имеет вид …
имеет вид …
 | 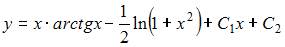 | ||
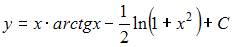 | |||
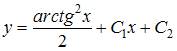 | |||
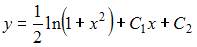 |
Решение:
Проинтегрируем последовательно обе части уравнения два раза: 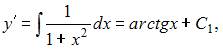
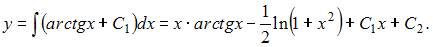
То есть общее решение примет вид 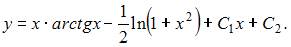
 ЗАДАНИЕ N 13 сообщить об ошибке
ЗАДАНИЕ N 13 сообщить об ошибке
Тема: Дифференциальные уравнения высших порядков, допускающие понижение порядка
Общее решение дифференциального уравнения 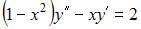 имеет вид …
имеет вид …
 | 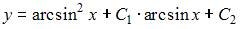 | ||
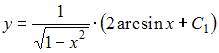 | |||
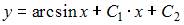 | |||
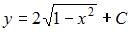 |
 ЗАДАНИЕ N 24 сообщить об ошибке
ЗАДАНИЕ N 24 сообщить об ошибке
Тема: Дифференциальные уравнения высших порядков, допускающие понижение порядка
Функция 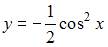 является решением дифференциального уравнения второго порядка …
является решением дифференциального уравнения второго порядка …
 | 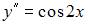 | ||
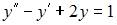 | |||
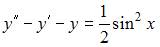 | |||
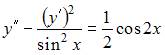 |
 ЗАДАНИЕ N 29 сообщить об ошибке
ЗАДАНИЕ N 29 сообщить об ошибке
Тема: Дифференциальные уравнения высших порядков, допускающие понижение порядка
Общее решение дифференциального уравнения 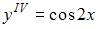 имеет вид …
имеет вид …
 | 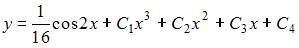 | ||
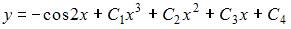 | |||
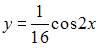 | |||
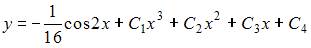 |
Решение:
Проинтегрируем последовательно обе части уравнения четыре раза: 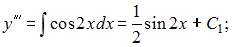
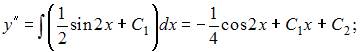
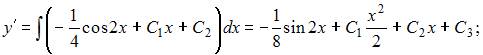
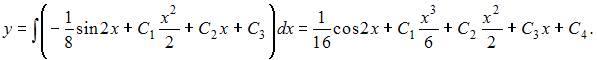
То есть общее решение можно записать в виде 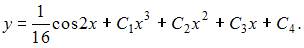
 ЗАДАНИЕ N 12 сообщить об ошибке
ЗАДАНИЕ N 12 сообщить об ошибке
Тема: Дифференциальные уравнения высших порядков, допускающие понижение порядка
Функция 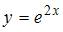 является решением дифференциального уравнения второго порядка …
является решением дифференциального уравнения второго порядка …
 | 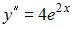 | ||
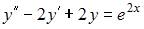 | |||
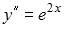 | |||
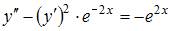 |
 ЗАДАНИЕ N 34 сообщить об ошибке
ЗАДАНИЕ N 34 сообщить об ошибке
Тема: Дифференциальные уравнения высших порядков, допускающие понижение порядка
Общее решение дифференциального уравнения 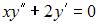 при
при 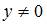 имеет вид …
имеет вид …
 | 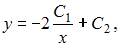 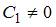 | ||
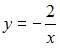 | |||
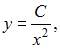 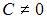 | |||
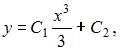 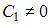 |
Решение:
Для решения дифференциального уравнения 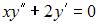 необходимо сделать замену
необходимо сделать замену 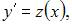
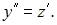 Тогда порядок этого уравнения понизится на одну единицу и оно примет вид
Тогда порядок этого уравнения понизится на одну единицу и оно примет вид 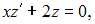
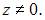
Решим это уравнение: 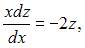
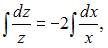
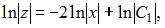
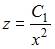 и
и 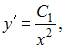 где
где 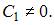
Следовательно, 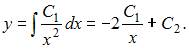
 ЗАДАНИЕ N 23 сообщить об ошибке
ЗАДАНИЕ N 23 сообщить об ошибке
Тема: Дифференциальные уравнения высших порядков, допускающие понижение порядка
Общее решение дифференциального уравнения 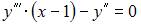 при
при 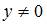 имеет вид …
имеет вид …
 | 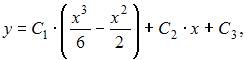 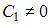 | ||
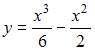 | |||
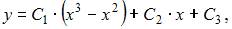 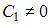 | |||
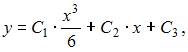 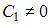 |
Решение:
Для решения дифференциального уравнения 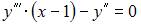 необходимо сделать замену
необходимо сделать замену 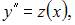
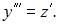 Тогда порядок этого уравнения понизится на две единицы и оно примет вид
Тогда порядок этого уравнения понизится на две единицы и оно примет вид 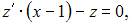
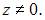
Это уравнение первого порядка с разделяющимися переменными. Разделив переменные, получим: 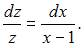 Тогда
Тогда 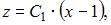 где
где 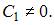 Сделав обратную замену, получим дифференциальное уравнение
Сделав обратную замену, получим дифференциальное уравнение 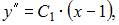
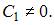
Проинтегрируем последовательно обе части уравнения два раза: 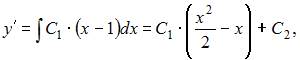
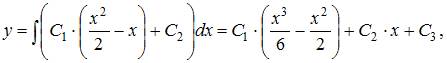
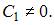
То есть общее решение имеет вид