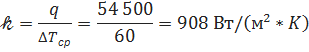Температурный напор по поверхности нагрева испарителя

Температура горячего теплоносителя – конденсирующегося водяного пара – остается неизменной и равной 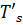=443 K. Следовательно, температурный напор в испарителе будет одинаковым по всей его поверхности и равным

ΔT= 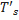-T₂=433-383=60 K

4. Коэффициент теплоотдачи 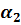со стороны кипящей флегмы

Для пузырькового режима кипения жидкости в большом объеме 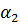[в Вт/(м²*К)] можно определить по следующей зависимости, предложенной Кружилиным: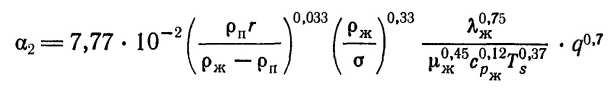

где 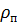, 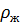– соответственно плотности паровой и жидкой фаз, кг/м³; r – теплота парообразования, Дж/кг; σ – поверхностное натяжение на границе раздела между жидкостью и паром, Н/м или кг/с²; λ_ж – теплопроводность жидкости, Вт/(кг*К); µ_ж – коэффициент динамической вязкости жидкости, Па*с; 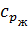– теплоемкость жидкости, Дж/(кг*К); 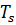– температура кипения флегмы, К; q – теплонапряжение поверхности нагрева, Вт/м².

Все физические параметры= в формуле определяются при температуре кипения флегмы 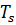= =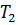383 K.

Плотность паровой фазы определим по уравнению Менделеева – Клапейрона:

= *

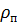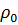
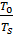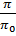
где 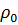– плотность пара при нормальных условиях, кг/м³; 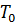= 273. К; π=1,47*10⁶ Па – давление в испарителе; 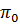=98,1*10³ Па;

Имеем:

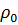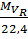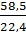= = = 2,6 кг/м³

После подстановки всех величин в формулу получим:

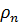= 2,6 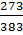* 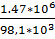= 28 кг/м³

Относительную плотность жидкости можно определить по формуле Мамедова:

=

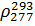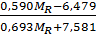
где 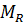= 61,6. Получим:

=

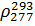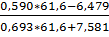
После этого по известным формулам или графикам нетрудно найти плотность остатка при температурах:

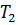= 383 K 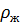= 528 кг/м³

T = 288 K 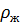= 602 кг/м³

Теплоту парообразования найдем как разность энтальпий паровой и жидкой фаз:

r = 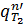- 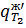= 690, 8 – 422, 9 = 267, 9 кДж/кг = 267, 9*10³ Дж/кг.

Поверхностное натяжение на границе раздела пар – жидкость определим по формуле Этвиша:

σ = (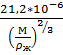

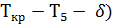
где M = M_R = 61,6 – средняя молекулярная масса остатка; 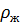= 528 кг/м³ – плотность остатка при температуре 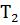= 383 К; Т_кр – критическая температура остатка, К; 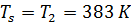; δ – постоянная, равная 7 К.

Найдем псевдокритическую температуру остатка по критическим температурам компонентов и их мольным долям в остатке:

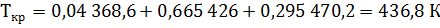
Подставляя найденные величины в формулу Этвиша, получим:

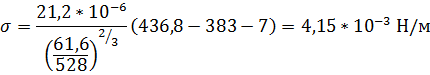
Коэффициент теплопроводности жидкости вычислим по формуле:

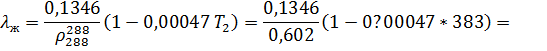
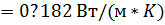
Коэффициент динамической вязкости жидкости как для смеси неассоциированных жидкостей можно определить по формуле:

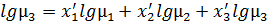
где 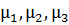– коэффициенты динамической вязкости компонентов жидкости.

Предварительно найдем для каждого из компонентов остатка значение µ при 383 К.

По графику имеем для пропана (С₃Н₈) при двух произвольно взятых температурах:

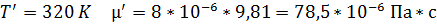
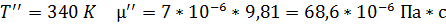
Для дальнейших расчетов воспользуемся формулой

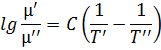
Здесь С – некоторая постоянная величина, которую легко найти из этой зависимости:

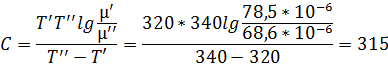
Пользуясь той же формулой, определим µ₁ при Т₂ = 383 К:

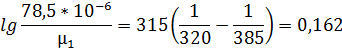
откуда µ₁ =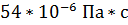

По тому же графику имеем для бутана (С₄Н₁₀):

при 290 K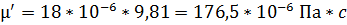

при 310 K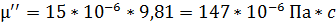

Расчеты, аналогичные сделанным для пропана, дают:

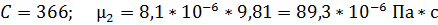
Для пентана (С₂Н₁₂) получим:

при 290 K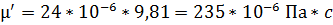

при 308 K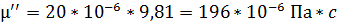

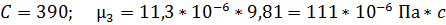
Теперь по формуле, приведенной выше, найдем коэффициент динамической вязкости для жидкого остатка в испарителе при :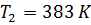

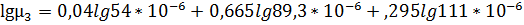
откуда

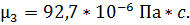
Теплоемкость жидкой фазы найдем по формуле:

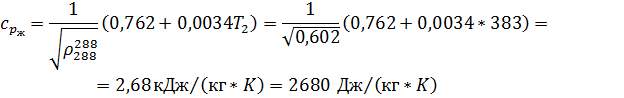
Подставляя все найденные выше значения в формулу для 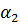, получим:

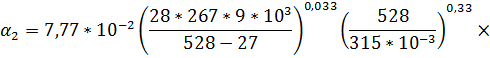
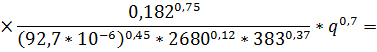
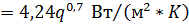
Таким образом, в зависимости от теплонапряжения поверхности за жидкую фазу везде принимается остаток R, а не флегма (V_R+R), 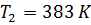именно остаток R находится в равновесии с паром V_R.

5. Коэффициент теплоотдачи 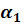со стороны конденсирующегося водяного пара

Для случая конденсации водяного пара внутри горизонтальных труб предложено уравнение

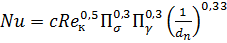
которое в рабочем виде записывается так:

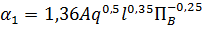
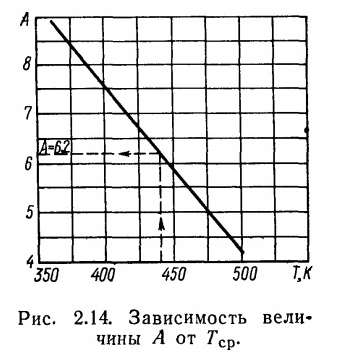
где А=φ(Т _ср) – коэффициент, зависящий от средней температуры конденсата и определяемый по графику (рис. 2.14); q – теплонапряжение поверхности нагрева испарителя, Вт/м²; l – длина трубы, м; d_B – внутренний диаметр трубы, м.

Средняя температура конденсата равна:

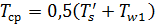
где 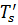- температура насыщенного пара, K; 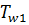– температура стенки со стороны конденсирующегося пара, K.

Температура 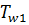, как правило, мало отличается от 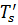, поэтому без большой погрешности можно принимать .

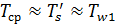По графику (рис. 2.14) при Т _ср = 443 К А=6,2. Тогда .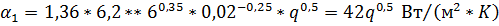

Коэффициент теплопередачи

С учетом тепловых сопротивлений стенки и загрязнений ее обеих поверхностей коэффициент теплопередачи определим из уравнения:

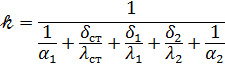
где 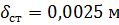– толщина стенки трубы; 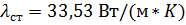– коэффициент теплопроводности материала стенки трубы; 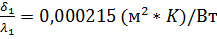– тепловое сопротивление загрязнения внутренней поверхности труб, - принимается как среднее значение для водяного пара и мягкой воды; 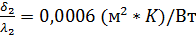– тепловое сопротивление загрязнения наружной поверхности трубы, - принимается как для светлого нефтепродукта.

Таблица 2

Величины	Результаты расчетов
q, Вт/м2 (принимается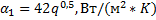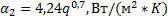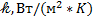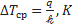). . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	30 000 7 266 5 766	50 000 9 408 8 226	70 000 11 088 10 473

Тогда

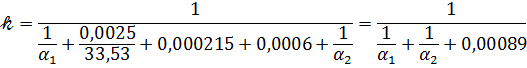
Так как 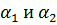являются функциями теплонапряжения q, величина которого неизвестна, то вычисление 𝓀 ведем методом постепенного приближения. Задаемся различными значениями q и для каждого из них находим 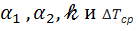. Результаты расчетов сведены в таблице 2.

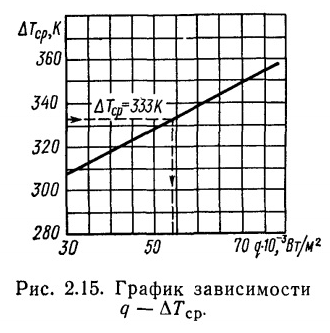
По данным этой таблицы строим график зависимости 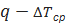(рис.2.15), называемый нагрузочной характеристикой испарителя.

Зная, что в рассчитываемом испарителе средний температурный напор 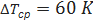, находим по графику (рис. 2.15) соответствующее теплонапряжение поверхности нагрева .

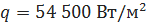Коэффициент теплопередачи в испарителе: