Прямое (декартово) произведение множеств. Бинарные (n-арные) отношения, их свойства.

Рассмотрим множества {1,2}и {2,1}.Они равны, так как состоят из одних и тех же элементов. Однако, в математике и технике приходится рассматривать и упорядоченные множества, то есть множества с заданным на них порядком следования элементов. Так, точки на плоскости А(1,2) и В(2,1) являются различными. Иногда, упорядоченную пару определяют следующим образом:

Определение 1. (a,b) 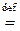{{a},{a,b}}, то есть под упорядоченной парой понимается множество, состоящее из двух множеств: неупорядоченной пары {a,b} и множества, состоящего из одного элемента, который считается первым.

Это определение предложил польский математик Казимеж Куратовский (1896-1980).

Очевидно, что:

1) ;

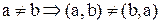2) .

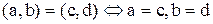Определение 2. Прямым (декартовым) произведением множеств А и В называется множество, обозначаемое А 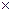В (читается: “A прямо на В”), и состоящее из всех упорядоченных пар (a,b), где 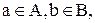то есть

.

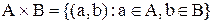Пример: А={1,2}; B={3,4}

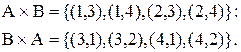
Из примера видно, что 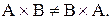Операция 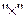не коммутативна.

Определение 3. Бинарным отношением между элементами множеств А и В или бинарным отношением, определенным на паре множеств А и В называется подмножество множества .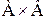

Бинарное отношение обозначается обычно большими буквами латинского алфавита R, S, T, либо малыми буквами греческого алфавита ,….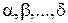

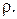
Определение 4. Прямым произведениеммножеств А₁, А₂, … , А_n называется множество 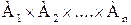, состоящее из всех упорядоченных n‑ок (a₁,a₂,…a_n) (из всех кортежей длины n), где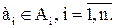

Определение 5. n-арным отношениеммежду элементами множеств А₁, А₂, … , А_n называется подмножество множества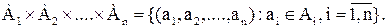

При n=1 отношение называется унарным, при n=2 отношение называется бинарным, при n =3 отношение называется тернарным и т. д.

Определение 6.Бинарное отношение между элементами множества А и А называется бинарным отношением на множестве А. То есть, это подмножество множества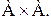

Множество 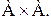обозначают также 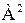и называют декартовым квадратом множества А.

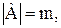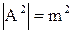Если то и .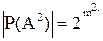

Определение 7. n-арным отношением на множестве Аназывается подмножество множества 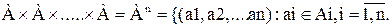Аⁿ называется n-ой декартовой степенью множества А.

Пример: Пусть А={1,2}, тогда 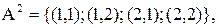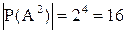и, следовательно, на множестве А можно задать 16 различных бинарных отношений. Выпишем некоторые из них:

1) Ø;

2) ;

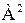3) 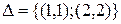-диагональ ;

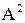4) {(1,2),(2,1)} и др.

Пусть -бинарное отношение на множестве А. Если 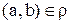, то говорят, что a и b находятся в отношении и пишут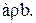

Определение 8.Бинарное отношение на множестве А называется рефлексивным, если 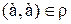для всех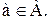

Замечание: Множество 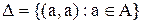называется диагональю множества 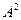. Отношение рефлексивно тогда и только тогда, когда .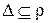

Определение 9.Бинарное отношение называется на множестве А симметричным, если из 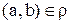следует, что 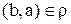, для всех a и b из множества А.

Определение 10.Бинарное отношение на множестве А называется транзитивным, если из 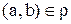и 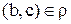, следует, что 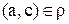для всех a, b и с из множества А.

Определение 11.Бинарное отношение называется антирефлексивным на множестве А, если 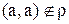для всех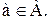

Определение 12.Бинарное отношение на множестве А называется антисимметричным, если из 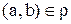и 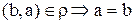для всех a и b из множества А.

Определение 13.Бинарное отношение называется связаннымна А, если для всех a и b из множества А выполняется одно и только одно из соотношений: a=b 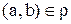или или .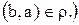

Примеры: 1) Отношение параллельности прямых на плоскости является рефлексивным, симметричным и транзитивным.

2) Отношение “меньше” на множестве действительных чисел является антирефлексивным, антисимметричным, транзитивным и связанным.

3) Отношение 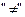на множестве действительных чисел является антирефлексивным и симметричным.

4) Отношение 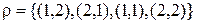на множестве натуральных чисел является симметричным и транзитивным, не является рефлексивным, не является антирефлексивным и не является связанным.

5) Отношение 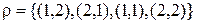на множестве 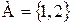является рефлексивным, симметричным и транзитивным, не является связанным.