Разработка математической модели и структурной схемы заданной системы.

Описание устройства и работы автоматической системы, разработка ее функциональной схемы.

На рисунке 1.1 представлен принцип регулирования производительности гидравлического мотора. Данная подсистема управления используется для управления транспортными средствами (изменения вращения выходных валов гидродвигателей, а следовательно, и скорости) имеющими отдельные приводы левого и правого расположения.

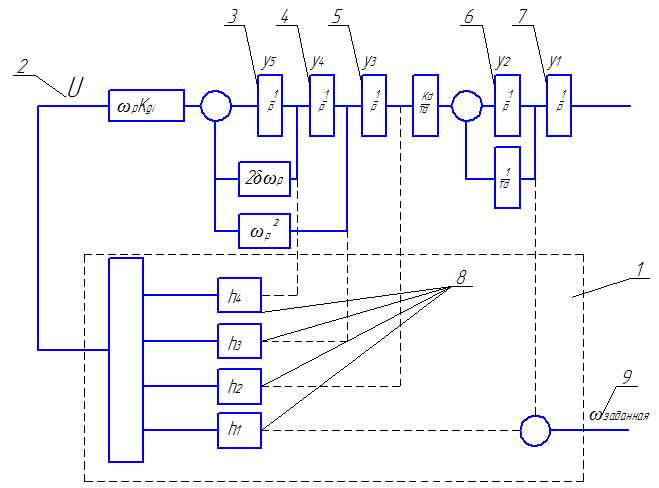
Рисунок 1.1 – Структурная схема регулирования гидравлического мотора

1 – контроллер; 2 – управляющее напряжение (U) электромагнита; 3 – скорость перемещения золотника (y5); 4 – перемещение золотника (y4); 5 – перемещение управляющего гидравлического цилиндра, отвечающего за наклон регулировочной шайбы(y3); 6 – угловая скорость гидравлического двигателя (y2); 7 – угол поворота выходного вала гидравлического двигателя (y1); 8 – коэффициенты управления (h1,h2,h3,h4); 9 – заданная угловая частота вращения выходного вала гидравлического двигателя.

Разработка математической модели и структурной схемы заданной системы.

Система «золотник — исполнительный механизм»

Гидравлическая система, состоящая из золотника и поршневого исполнительного механизма, может быть использована в качестве примера для рассмотрения методики вывода точных дифференциальных уравнений или передаточных функций. Система, показанная на рисунке 2.1, состоит из четырехходового золотника, исполнительного механизма с поршнем и инерционной нагрузки. К центральному буртику золотника от внешнего источника подастся рабочая жидкость под постоянным давлением.

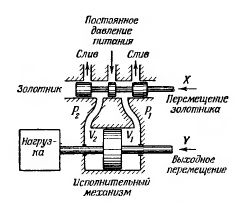
Рисунок2.1 – Гидравлическая система, состоящая из четырехходового золотника и исполнительного механизма.

Если золотник стоит в средней позиции, то рабочая жидкость не поступает к исполнительному механизму и, следовательно, скорость поршня и нагрузки будет равна нулю. Когда же золотник смещен в одном из направлений, поршень и нагрузка будут двигаться со скоростью, пропорциональной величине перемещения золотника. При смещении золотника в противоположном направлении от средней позиции жидкость будет поступать в другую полость силового цилиндра и произойдет реверс движения нагрузки. Перепад давлений на поршне исполнительного механизма, возникающий при смещении золотника со средней позиции, создаст силу, необходимую для движения нагрузки. Уравнение системы, помимо инерционной нагрузки, будет также учитывать вязкое трение на поршне, сжимаемость жидкости и утечки через золотник. Вывод основан на определении перемещений золотника, необходимых для обеспечения различных видов движения нагрузки: 1) для создания движения нагрузки с требуемой скоростью; 2) для обеспечения ускоренною движения нагрузки; 3) для обеспечения заданной степени изменении ускорения нагрузки и создания расхода, идущего на компенсацию сжимаемости жидкости. Для вывода используются следующие обозначения: X – перемещение золотника, см; Y – перемещения поршня и нагрузки, см; X₁ – перемещение золотника, необходимое для создания скорости, см; Х₂ перемещение золотника, необходимое для обеспечения ускоренного движения нагрузки, см; Х₃ – перемещение золотника, необходимое для создания расхода, идущего на компенсацию сжимаемости жидкости, см; C₁ коэффициент усиления по скорости, (см/сек)/см; α – коэффициент вязкого трения нагрузки и поршня, кг/(см/сек); K_Q0 – коэффициент усиления по расходу при нулевом перепаде давлений па поршне, (см³/сек)/см; С₂ – коэффициент усиления по усилию, кг/см, s = d/dt комплексный оператор; М – масса нагрузки и поршня, кг·сек²/см; А–площадь поршня, см²; V – эффективный объем жидкости, находящейся в системе, см³ (V составляет половину общего объема жидкости, заключенной между золотником и поршнем); V_i – объем жидкости, находящейся с одной стороны поршня, см³, V₁ – объем жидкости, находящейся с другой стороны поршня, см³; К_р – коэффициент усиления по давлению, (кг/см²)/см; Р₁ – изменение давления с одной стороны поршня, кг/см²; Р₂ – изменение давления с другой стороны поршня, кг/см²; H – перепад давлений на поршне, кг/см²; В – объемный модуль упругости жидкости, кг/см²; ω_р – резонансная частота, рад/с; δ – коэффициент демпфирования (безразмерная величина).

При данном перемещении золотника поршень и нагрузка будут двигаться с определенной скоростью. Это соотношение можно записать следующим образом:

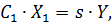(2.1)

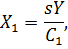(2.2)

Коэффициент усиления по скорости С₁ получается из коэффициента K_Q0, так как при наличии только инерционной нагрузки максимум скорости обычно возникает при нулевом перепаде давлений па поршне:

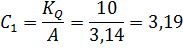(2.3)

Однако в выражении (2.3) не учтено дополнительное перемещение золотника, требующееся для преодоления вязкого трения поршня и нагрузки α. Чтобы учесть вязкое трение, нужно использовать коэффициент усиления по усилию С₂.

Таким образом, выражение для перемещения золотника, которое требуется для создания заданной скорости движения нагрузки, имеет вид

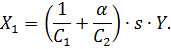(2.4)

Коэффициент усиления по усилию можно выразить через коэффициент усиления по давлению K_р:

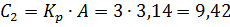(2.5)

Сила, необходимая для создания ускорения инерционной нагрузки, определяется по второму закону Ньютона:

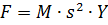(2.6)

С другой стороны, эту силу можно выразить через перемещение золотника и коэффициент усиления по усилию

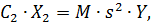(2.7)

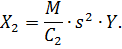(2.8)

Для изменения ускорения нагрузки должна быть изменена скорость возрастания или убывания по времени давлений в полостях силового цилиндра. Так как жидкость сжимаема, то для того, чтобы изменить давление в полости, через золотник нужно пропустить расход, компенсирующий сжимаемость. Величина этого расхода зависит от объема жидкости в полости и от объемного модуля упругости. Для одной полости можно записать:

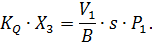(2.9)

Считая, что золотник симметричен, для второй полости имеем:

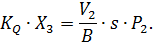(2.10)

Если допустить, что изменение перепада давлений на поршне равно сумме изменений давлений в полостях, то можно написать:

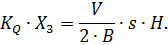(2.11)

Коэффициент 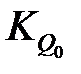, выразим через коэффициент усиления по скорости C₁

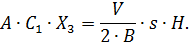(2.12)

Перепад давлений на поршне H можно выразить через силу, необходимую для создания ускорения инерционной нагрузки, и силу, идущую на преодоление вязкого трения

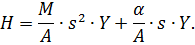(2.13)

Объединяя уравнения (2.12) и (2.13), получим:

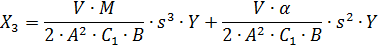(2.14)

Полное перемещение золотника, обеспечивающее все заданные случаи движения нагрузки, получается при суммировании уравнений(2.4), (2.8) и(2.14), т. е.:

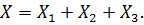(2.15)

Следовательно,

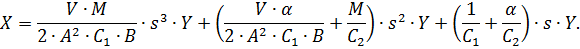(2.16)

Передаточная функция, полученная из уравнения (2.16), будет иметь вид:

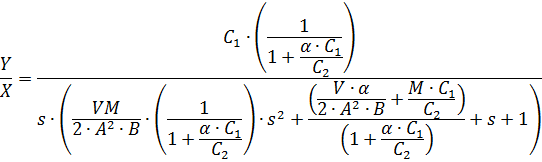(2.17)

Наличие колебательного звена в передаточной функции означает, что гидравлическая система «золотник — исполнительный механизм» является системой резонансного типа, подобно механической системе «пружина—масса». Следовательно, для такой системы можно записать выражения для резонансной частоты и коэффициента демпфирования

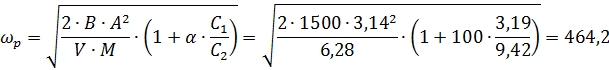(2.18)

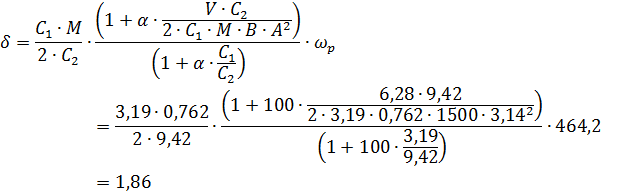(2.19)

Передаточную функцию с учетом уравнений (2.18) и (2.19) можно представить как:

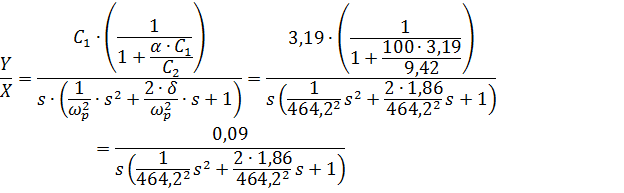(2.20)

Коэффициенты уравнения или передаточной функции сервомеханизма «золотник – исполнительный механизм» можно вычислить, используя постоянные коэффициенты системы. Сила вязкого трения и коэффициенты усиления золотника по расходу и давлению могут быть замерены, если для данной системы эти величины не известны. Характеристики золотника обычно нелинейны. Однако указанные коэффициенты золотника можно линеаризировать, считая, что границы рабочего диапазона не должны приближаться к точкам насыщения.

Коэффициент усиления по давлению К_р определяет величину изменения давления в полости силового цилиндра на единицу перемещения золотника. Использование методики, для определения коэффициентов усиления золотника по расходу и давлению, обусловливает получение линеаризированной передаточной функции системы «золотник– исполнительный механизм». Следует заметить, что хотя в рассматриваемом сервомеханизме величина вязкого демпфирования и превышает демпфирование, обусловленное утечками, его влияние на резонансную частоту системы весьма незначительно.

Когда поршень находится в крайних положениях, резонансная частота возрастает незначительно, и этим изменением обычно пренебрегают.

Система с регулируемым гидродвигателем.

Характерная особенность регулируемого гидродвигателя заключается в том, что управление мощностью, подводимой к нагрузке, осуществляется непосредственно внутри исполнительного двигатели за счет изменении его удельного объема. При этом изменяется момент, который развивает гидродвигатель. Этот метод позволяет использовать один источник гидравлического питания для приведения в действие нескольких гидравлических приводов. Регулируемый гидродвигатель схематически показан на рисунке 4.3.

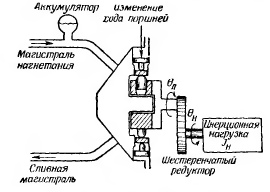
Рисунок 4.3 – Регулируемый гидродвигатель.

Развиваемый им момент является функцией перемещения поршня управляющего органа. Расход рабочей жидкости, поступающей к гидродвигателю, пропорционален требуемой скорости вращения выходного вала и величине перемещения поршня управляющего органа. Питание регулируемого гидродвигателя, осуществляется от источника с постоянным давлением в нагнетающей магистрали. Для любого хода поршня гидродвигатель в установившемся режиме работы будет иметь скорость, при которой развиваемый им момент равен моменту сопротивлении от вязкого трения. При изменении хода поршня возникает ускорение или торможение нагрузки. Если при торможении нагрузки поршень управляющего органа переходит через нуль и отклоняется в другую сторону, гидродвигатель будет работать как насос, перекачивая рабочую жидкость из сливной магистрали обратно в напорную. Уравнение и передаточная функция сервомеханизма этого типа могут быть выведены, исходя из баланса моментов на валу гидродвигателя:

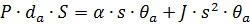(2.21)

где Р – давление подачи, кг/см²; S – ход поршня в процентах от полного ходя; α – коэффициент вязкого трения гидродвигателя и нагрузки, кг·см/(рад/сек); J – момент инерции гидродвигателя и нагрузки, кг·см·с²; 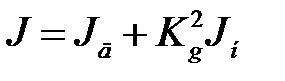; K_g – передаточное отношение θ_н/θ_д; s – комплексный оператор; θ_д – угловое перемещение выходного вала гидродвигателя, рад; d_д – удельный объем гидродвигателя, см³/рад.

Из дифференциального уравнения (2.21) может быть получена следующая передаточная функция:

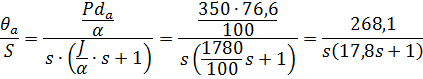(2.22)

Как можно заметить из рассмотрения передаточной функции, в этом типе сервомеханизма отсутствует гидравлический резонанс. Это объясняется тем, что управление и преобразование гидравлической энергии в механическую происходит в одной и той же гидравлической машине. Здесь нет гидравлической пружины или объемов жидкости между управляющим и управляемым органами как в сервомеханизмах «насос – гидродвигатель» и «золотник - исполнительный механизм». Наличие одной, но большой постоянной времени обусловливает характер управлении, отличный от того, который используется в обычных приводах. Чтобы обеспечить высококачественные характеристики и высокую точность работы, привод должен иметь обратную связь, охватывающую элемент, который создает постоянную времени. Обратная связь может быть либо механико-гидравлической, либо электрической.

Изменение хода поршней управляющего органа осуществляется механически или с помощью электропривода в зависимости от применения. Однако из-за наличия усилия, которое надо приложить, чтобы перемещать управляющий орган, что необходимо во всех типах регулируемых гидродвигателей. оптимальное управление обеспечивается с помощью вспомогательного золотникового клапана. Этот клапан может получать гидравлическое питание от того же источника, что и гидродвигатель.

Реакция системы на изменение момента нагрузки полностью зависит от быстроты перемещения управляющего органа. Поэтому необходимо, чтобы контур управления имел высокий коэффициент усиления и высокую чувствительность. Это обстоятельство налагает на управляющие устройства более высокие требования, чем в обычных системах «насос – гидродвигатель».