Жай спектрлі сызықтық операторлар
Анықтама. Векторлық кеңістіктегі  сызықтық операторының барлық меншікті мәндерінің жиыны сол оператордың спектрі деп аталады және Sp
сызықтық операторының барлық меншікті мәндерінің жиыны сол оператордың спектрі деп аталады және Sp  деп белгіленеді. Сонда
деп белгіленеді. Сонда
Sp  =
= 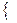

 F |
F | 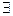 a
a 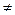 0
0  V
V 
 (a) =
(a) =  а
а 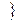
Спектрдің элементтерінің саны п – нен аспайды ( п = dimV).
Анықтама. Егер спектрдің элементтерінің саны дәл п – ға тең болса, онда оны жай спектр деп атайды.
Лемма. Сызықтық оператордың әртүрлі  ,
, 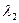 ,...,
,...,  – меншікті мәндеріне сәйкес келетін а
– меншікті мәндеріне сәйкес келетін а  ,а
,а  ,...,а
,...,а 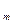 – меншікті векторлары СБ-сыз болады.
– меншікті векторлары СБ-сыз болады.
Дәлелдеу. Берілгені бойынша  (a
(a 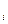 ) =
) = 
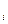 а
а 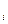 , i=1, 2,..., m.
, i=1, 2,..., m.
Лемманы m арқылы индукция әдісімен дәлелдейміз.
Индукция негізі: m = 1 болғанда  меншікті мәніне сәйкес келетін меншікті вектор а
меншікті мәніне сәйкес келетін меншікті вектор а  . Жалғыз вектор, әрине, сызықтық байланыссыз болады. Онда бұл жағдайда лемма дұрыс.
. Жалғыз вектор, әрине, сызықтық байланыссыз болады. Онда бұл жағдайда лемма дұрыс.
Индукциялық болжау: m = к болғанда лемма дұрыс делік, яғни  ,
, 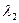 ,...,
,..., 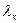 – әртүрлі меншікті мәндерге сәйкес а
– әртүрлі меншікті мәндерге сәйкес а  ,а
,а  ,...,а
,...,а  меншікті векторлары СБ-сыз болсын. Бұл
меншікті векторлары СБ-сыз болсын. Бұл 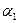 а
а  +
+ 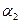 а
а  +...+
+...+  а
а  = 0
= 0 
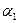 =
= 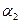 =...=
=...=  = 0 деген сөз.
= 0 деген сөз.
Индукциялық қадам: m = к +1 болғанда лемманың дұрыстығын көрсетейік. Әртүрлі  ,
, 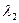 ,...,
,...,  меншікті мәндерге сәйкес келетін а
меншікті мәндерге сәйкес келетін а  ,а
,а  ,...,а
,...,а 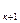 меншікті векторларының сызықтық комбинациясын қарастырайық.
меншікті векторларының сызықтық комбинациясын қарастырайық.
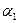 а
а  +
+ 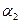 а
а  +...+
+...+  а
а  +
+  а
а 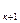 = 0(*)
= 0(*)
Теңдіктің екі жағындағы векторлардың  сызықтық операторының нәтижесіндегі образдарын табамыз.
сызықтық операторының нәтижесіндегі образдарын табамыз.
 (
( 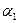 а
а  +
+ 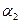 а
а  +...+
+...+  а
а  +
+  а
а 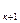 ) =
) =  (0)
(0)  |
|  -с.оп., а
-с.оп., а 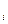 -менш.вект.|
-менш.вект.| 
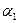
 а
а  +
+ 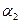
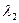 а
а  +...+
+...+ 
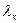 а
а  +
+ 
 а
а 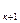 = 0(**)
= 0(**)
(*) өрнегін  –ге көбейтіп, (**) өрнегінен мүшелеп алып тастаймыз:
–ге көбейтіп, (**) өрнегінен мүшелеп алып тастаймыз:
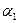 (
(  -
-  )а
)а  +
+ 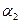 (
( 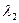 -
-  )а
)а  +...+
+...+  (
( 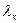 -
-  )а
)а  = 0
= 0  |инд.болж.бойынша|
|инд.болж.бойынша| 
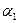 =
= 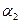 =...=
=...=  = 0 (себебі,
= 0 (себебі, 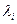 –лер әртүрлі). Осыны (**)-ға қойсақ,
–лер әртүрлі). Осыны (**)-ға қойсақ,

 а
а 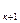 = 0 теңдігін аламыз. Бұдан
= 0 теңдігін аламыз. Бұдан  =0 (
=0 (  – менш.мән, ол
– менш.мән, ол 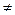 0). Сонда,(*)өрнегіндегі барлық
0). Сонда,(*)өрнегіндегі барлық  =0, i=1,2,...,к+1.Сондықтан а
=0, i=1,2,...,к+1.Сондықтан а  ,...,а
,...,а 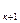 –СБ-сыз.
–СБ-сыз.
Онда, математикалық индукция принципі бойынша лемма кезкелген m үшін дұрыс. Д.к.о.
Салдар. Егер сызықтық оператордың спектрі жай спектр болса, онда барлық меншікті мәндерге сәйкес келетін меншікті векторлар векторлық кеңістіктің базисін құрайды.
Дәлелдеуі леммадан шығады (өздеріңіз дәлелдеңіз).
Теорема. Егер векторлық кеңістіктің базисі СБ-сыз п меншікті вектордан тұрса, онда сызықтық оператордың осы базистегі матрицасы диагональ матрица болады. Және керісінше, егер сызықтық оператордың қандайда-бір базистегі матрицасы диагональ болса, онда осы базистің барлық векторлары меншікті векторлар болады.
Дәлелдеу. Айталық, V  кеңістігінің базисі а
кеңістігінің базисі а  , а
, а  ,..., а
,..., а  –
–  сызықтық операторының СБ-сыз п меншікті векторларыболсын. Сонда
сызықтық операторының СБ-сыз п меншікті векторларыболсын. Сонда

 ...,
...,  . Онда базистің қасиеті бойынша:
. Онда базистің қасиеті бойынша:
 (1)
(1)
Бұл теңдіктерден, а  ,а
,а  ,...,а
,...,а  базисіндегі
базисіндегі  сызықтық операторының матрицасы –
сызықтық операторының матрицасы –  (2) түріндегі диагональ матрица болатыны шығады.
(2) түріндегі диагональ матрица болатыны шығады.
Кері тұжырымды дәлелдейік. Айталық қандайда-бір а  , а
, а  ,..., а
,..., а  базисіндегі
базисіндегі  сызықтық операторының матрицасы (2) түріндегі диагональ матрица болсын. Онда ( §5, (2¢) формуласы бойынша)
сызықтық операторының матрицасы (2) түріндегі диагональ матрица болсын. Онда ( §5, (2¢) формуласы бойынша)
 немесе, матрицаларды көбейтсек,
немесе, матрицаларды көбейтсек,  , яғни базистің а
, яғни базистің а  ,...,а
,...,а  векторлары
векторлары  сызықтық операторының меншікті векторлары болады. Д.к.о.
сызықтық операторының меншікті векторлары болады. Д.к.о.
Дәлелденген лемма, салдар, теоремадан мынадай қорытынды аламыз:
Егер өрісте берілген векторлық кеңістіктегі сызықтық оператордың спектрі жай спектр болса, онда ол оператордың матрицасы диагональ түрге келтіріледі.
Егер де спектрдің элементтерінің саны п-нен кіші болса, басқаша айтқанда, характеристикалық теңдеудің кейбір түбірлері еселі түбірлер болса, онда оператордың матрицасының диагональ түрге келтірілу-келтірілмеуі СБ-сыз меншікті векторлардың санына байланысты болады. Егер мұндай меншікті векторлар саны п-ға тең болса, матрица диагональ түрге келтіріледі, ал ол сан п-нен кем болса – келтірілмейді. Негізінде, сызықтық оператордың характеристикалық теңдеуінің түбірлерінің арасында өзара теңдері болған жағдайда, оператордың матрицасын диагональ түрге келтіру мәселесі күрделі мәселе.
Мысал. 1). R 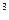 векторлық кеңістігінде
векторлық кеңістігінде  сызықтық операторы қандайда-бір базисте мынадай матрицамен берілсін:
сызықтық операторы қандайда-бір базисте мынадай матрицамен берілсін: 
Жаңа базиске көшу арқылы осы оператордың матрицасын диагональ түрге келтіруге бола ма? Болса, сол базисті және сәйкес матрицаны табыңыз.
Шешуі.

Сонда,  ,
,  ,
,  , меншікті мәндердің саны 3-ке тең, кеңістіктің өлшеміне тең, онда матрица диагональ түрге келтіріледі.
, меншікті мәндердің саны 3-ке тең, кеңістіктің өлшеміне тең, онда матрица диагональ түрге келтіріледі.
Әрбір меншікті мәнге сәйкес меншікті векторларды табамыз. Вектордың координаталары  болса, §10-ғы (11;4) жүйе
болса, §10-ғы (11;4) жүйе
 (11;4
(11;4  ) өрнегінен алынады. Әрбір меншікті мәнді осыған қоямыз.
) өрнегінен алынады. Әрбір меншікті мәнді осыған қоямыз.

 . Мынадай жүйе аламыз:
. Мынадай жүйе аламыз:

 сандарына көбейтіп, қосып, Гаусс әдісімен шешеміз.
сандарына көбейтіп, қосып, Гаусс әдісімен шешеміз.
 х
х  , х
, х  – бас айнымалылар, х
– бас айнымалылар, х 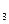 – бос айнымалы.
– бос айнымалы.
 бұл – жүйенің жалпы шешуі.
бұл – жүйенің жалпы шешуі.
Бос айнымалыға өзіміз мән береміз: х 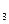 =5, онда х
=5, онда х  –2, х
–2, х  4. Сонда,
4. Сонда,  меншікті мәніне сәйкес меншікті вектор а
меншікті мәніне сәйкес меншікті вектор а  (–2, 4, 5), яғни
(–2, 4, 5), яғни  .
.

 .
.  жүйесін аламыз.
жүйесін аламыз.
Гаусс әдісімен шешеміз:  ,
,  бас,
бас,  бос айнымалы.
бос айнымалы.
 – жүйенің жалпы шешуі. Бос айнымалыға мән береміз: х
– жүйенің жалпы шешуі. Бос айнымалыға мән береміз: х 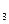 =1, онда
=1, онда
х  0, х
0, х  1. Сонда,
1. Сонда,  меншікті мәніне сәйкес меншікті вектор
меншікті мәніне сәйкес меншікті вектор
а  (0, 1, 1), яғни
(0, 1, 1), яғни  .
.

 .
.  жүйесін аламыз.
жүйесін аламыз.
Гаусс әдісімен шешеміз:  ,
,  бас,
бас,  бос айнымалы. Бас айнымалылар бос айнымалыға тәуелді емес:
бос айнымалы. Бас айнымалылар бос айнымалыға тәуелді емес:  Бос айнымалыға мән береміз: х
Бос айнымалыға мән береміз: х 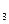 =1. Сонда,
=1. Сонда,  меншікті мәніне сәйкес меншікті вектор
меншікті мәніне сәйкес меншікті вектор
а  (0, 0, 1), яғни
(0, 0, 1), яғни  .
.
Жоғарыдағы лемманың салдары бойынша, табылған а  ,а
,а  ,а
,а 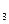 векторлары базис құрайды және берілген
векторлары базис құрайды және берілген  сызықтық операторының осы базистегі матрицасы диагональ
сызықтық операторының осы базистегі матрицасы диагональ  матрицасы болады.
матрицасы болады.
Төмендегі 2 мысал спектрдің элементтерінің саны кеңістіктің өлшемінен кем болған жағдайға берілген. Қай жағдайда сызықтық оператордың матрицасын диагональ түрге келтіруге болады? Болған жағдайда диагональ матрицаны табыңыз.
2).  ; 3).
; 3).  ;
;
