Непараметрические критерии: Критерий согласия Пирсона (описание)

Возможно, что расхождение частот неслучайно (значимо) и объясняется тем, что теоретические частоты вычислены исходя из неверной гипотезы о нормальном распределении генеральной совокупности

Критерий Пирсона отвечает на поставленный выше вопрос. Правда, как и любой критерий, он не доказывает справедливость гипотезы, а лишь устанавливает на принятом уровне значимости ее согласие или несогласие с данными наблюдений.

Итак, пустьпо выборке объема п получено эмпири­ческое распределение:

варианты……. хi х1 х2 … хs

эмп. частоты... пi п1 п2 ... пs

Допустим, что в предположении нормального распре­деления генеральной совокупности вычислены теорети­ческие частоты п'i (например, так, как в следующем па­раграфе). При уровне значимости а требуется проверить нулевую гипотезу: генеральная совокупность распреде­лена нормально.

В качестве критерия проверки нулевой гипотезы при­мем случайную величину

(*)

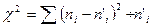.Эта величина случайная, так как в различных опытах она принимает различные, заранее не известные значе­ния. Ясно, что чем меньше различаются эмпирические и теоретические частоты, тем меньше величина критерия (*), и, следовательно, он в известной степени характеризует близость Эмпирического и теоретического распределений.

Заметим, что возведением в квадрат разностей частот устраняют возможность взаимного погашения положи­тельных и отрицательных разностей. Делением на 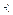до­стигают уменьшения каждого из слагаемых; в против­ном случае сумма была бы настолько велика, что при­водила бы к отклонению нулевой гипотезы даже и тогда. когда она справедлива. Разумеется, приведенные сооб­раженияне являются обоснованием выбранного крите­рия, а лишь пояснением.

Доказано, что при п—>∞ закон распределения слу­чайной величины (*) независимо от того, какому закон распределения подчинена генеральная совокупность, стре­мится к закону распределения χ² с k степенями свободы Поэтому случайная величина (*) обозначена через χ², :

сам критерий называют критерием согласия «хи квадрат»

Число степеней свободы находят по равенству k == s—1—г, где s—число групп (частичных интервалов выборки; г—число параметров предполагаемого распре­деления, которые оценены по данным выборки.

В частности, если предполагаемое распределение—нормальное, то оценивают два параметра (математическское ожидание и среднее квадратическое отклонение), поэтому г =2 и число степеней свободы k==s—1—r =s—1—2=

=s—3.

Если, например, предполагают, что генеральная сово­купность распределена по закону Пуассона, то оцени­вают один параметр К, поэтомуг==1 и k=s—2.

Поскольку односторонний критерий более «жестко» отвергает нулевую гипотезу, чем двусторонний, построим правостороннюю критическую область, исходя из требо­вания, чтобы вероятность попадания критерия в эту об­ласть в предположении справедливости нулевой гипотезы была равна принятому уровню значимости а:

.

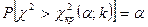Таким образом, правосторонняя критическая область определяется неравенством 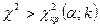, а область принятия нулевой гипотезы—неравенством .

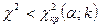Обозначим значение критерия, вычисленное по дан­ным наблюдений, через 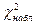и сформулируем правило проверки нулевой гипотезы.