Обзор основных элементарных функций.
Линейная функция
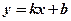 ,
,
где 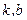 – константы.
– константы. 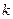 – угловой коэффициент наклона прямой,
– угловой коэффициент наклона прямой, 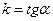 , где
, где 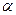 – угол между прямой и положительным направлением оси
– угол между прямой и положительным направлением оси 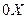 (см. рис.1).
(см. рис.1).
|
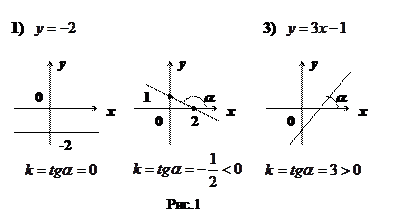
Квадратичная функция
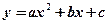 ,
,
где 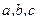 – константы. График - парабола. Если
– константы. График - парабола. Если 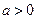 , то ветви параболы направлены вверх, если
, то ветви параболы направлены вверх, если 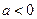 – то вниз.
– то вниз.
Корни функции:
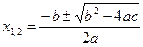
Координаты 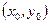 вершины параболы:
вершины параболы:
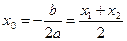 ;
; 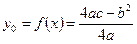
Заметим, что если 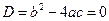 , то
, то 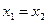 (два совпадающих корня!).
(два совпадающих корня!).
Пример.
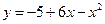 . Находим корни функции из уравнения
. Находим корни функции из уравнения 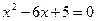 :
: 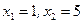 . Координаты вершины этой параболы:
. Координаты вершины этой параболы:
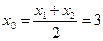 ;
; 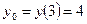 . (см. рис.2).
. (см. рис.2).
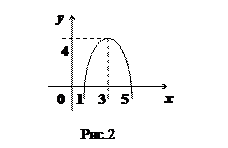
Дробно-линейная функция
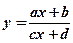
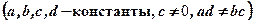 .
.
График – гипербола. Частный случай: 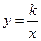
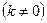 – "обратная пропорциональность" (см. рис. 3).
– "обратная пропорциональность" (см. рис. 3).
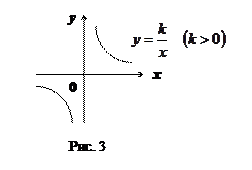
Показательная функция
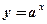
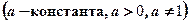 (см. рис.4).
(см. рис.4).
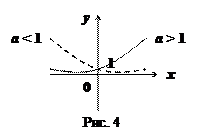
Логарифмическая функция
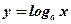
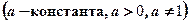 (см. рис.5).
(см. рис.5).

Степенная функция
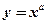 (
( 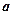 – любое действительное число)
– любое действительное число)
1) 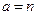 (
( 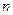 – натуральное число) (см. рис.6):
– натуральное число) (см. рис.6):
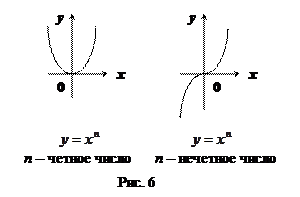
2) 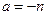 (
( 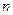 – натуральное число) (см. рис.7):
– натуральное число) (см. рис.7):

3) 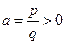 – несократимая дробь (см. рис.8):
– несократимая дробь (см. рис.8):
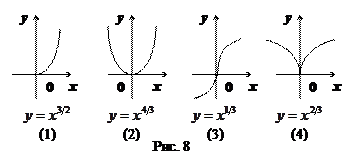
При построении таких графиков надо учитывать четность 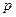 и
и 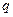 , а также соотношение между
, а также соотношение между 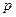 и
и 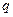 :
: 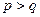 или
или 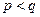 . Например, если
. Например, если 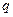 чётно, то
чётно, то 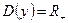 (см. рис.(1)); если
(см. рис.(1)); если 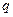 нечётно, то
нечётно, то 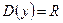 (см. рис. (2) – (4)). Если
(см. рис. (2) – (4)). Если 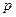 чётно, то
чётно, то 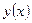 – чётная функция; если
– чётная функция; если 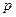 нечётно, то
нечётно, то 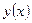 – нечётная функция. Если
– нечётная функция. Если 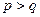 , то при
, то при 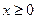 график функции ведет себя, как график функции
график функции ведет себя, как график функции 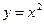 , а если
, а если 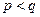 , то – как график функции
, то – как график функции 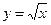 .
.
Функция
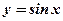 (см. рис.9)
(см. рис.9)

Нечетная периодическая функция с периодом 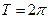 . Полезно помнить, что:
. Полезно помнить, что:
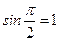 ;
; 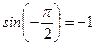 ;
; 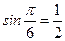 ;
; 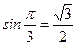 ;
;
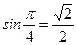 ;
; 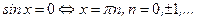 .
.
Функция
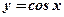 (см. рис.10)
(см. рис.10)
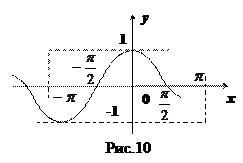
Четная периодическая функция с периодом 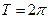 . Полезно помнить, что:
. Полезно помнить, что:
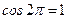 ;
; 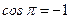 ;
; 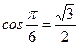 ;
; 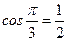 ;
;
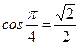 ;
; 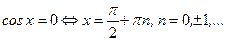 .
.
Функция
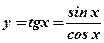 (см. рис.11):
(см. рис.11):
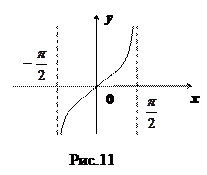
Нечетная периодическая функция с периодом 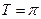 . Значения функции
. Значения функции 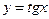 в точках
в точках 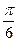 ;
; 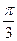 ;
; 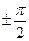 ;
; 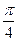 и т.д. вычисляются по значениям функций
и т.д. вычисляются по значениям функций 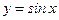 и
и 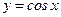 .
.
Функция
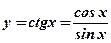 (см. рис.12):
(см. рис.12):
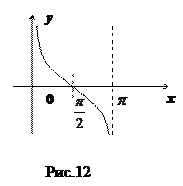 |
Нечетная периодическая функция с периодом 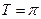 . Значения функции
. Значения функции 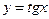 в точках
в точках 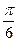 ;
; 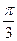 ;
; 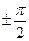 ;
; 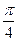 и т.д. вычисляются по значениям функций
и т.д. вычисляются по значениям функций 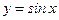 и
и 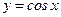 .
.
Функция
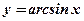 (арксинус числа
(арксинус числа 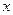 – это такое число
– это такое число 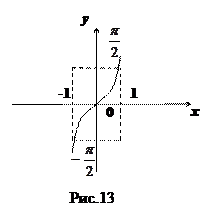
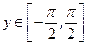 , что
, что 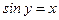 ) (см. рис.13):
) (см. рис.13):
Функция
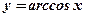 (арккосинус числа
(арккосинус числа 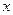 – это такое число
– это такое число 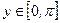 , что
, что 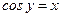 ) (см. рис.14):
) (см. рис.14):
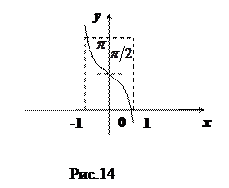 |
Функция
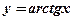 (арктангенс числа
(арктангенс числа 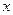 – это такое число
– это такое число 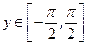 , что
, что 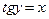 ) (см. рис.15):
) (см. рис.15):
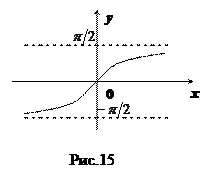
Функция
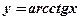 (арккотангенс числа
(арккотангенс числа 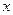 – это такое число
– это такое число 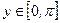 , что
, что 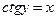 ) (см. рис.16):
) (см. рис.16):
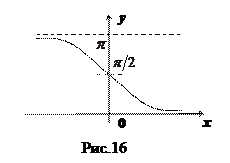
Примеры:
1)Найти 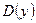 для следующих функций:
для следующих функций:
а) 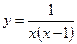 .
.
▲ Т.к. знаменатель дроби, задающей функцию, не должен равняться нулю, то
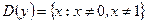 .
.
б) 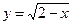 .
.
▲ Т.к. функция задается при помощи корня чётной степени из выражения 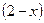 , то
, то 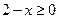 , и
, и
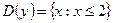 .
.
2)Выяснить чётность следующих функций:
а) 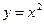 .
.
▲ Функция 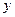 – чётная, т.к.
– чётная, т.к. 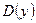 симметрична относительно точки
симметрична относительно точки 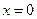 и
и 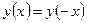 для
для 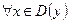 .
.
б) 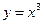 .
.
▲ Функция 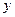 – нечётная, т.к.
– нечётная, т.к. 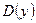 симметрична относительно точки
симметрична относительно точки 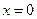 и
и 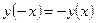 для
для 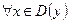 .
.
в) 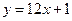 .
.
▲ Функция 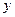 не является ни четной, ни нечетной, т.к.
не является ни четной, ни нечетной, т.к. 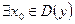 :
: 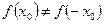 и
и 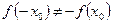 . В качестве
. В качестве 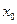 можно взять, например
можно взять, например 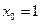 . (Заметим, что
. (Заметим, что 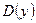 симметрична относительно точки
симметрична относительно точки 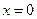 ).
).
г) 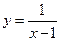 .
.
▲ Функция 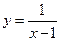 не является ни четной, ни нечетной, т.к.
не является ни четной, ни нечетной, т.к. 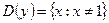 не симметрична относительно точки
не симметрична относительно точки 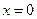 .
.
3)Найти значение функции в заданной точке 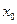 :
:
а) 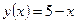 ,
, 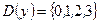 ,
, 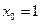 ;
; 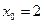 .
.
▲ 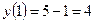 ,
, 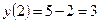 .
.
б) 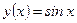 ,
, 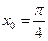 .
.
▲ 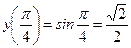 .
.
Задачи для самостоятельного решения.
I. Найти 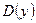 :
:
1) 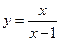 ; 2) ; 2) 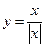 ; 3) ; 3) 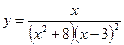 ; 4) ; 4) 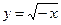 ; 5) ; 5) 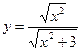 ; 6) ; 6) 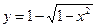 ; 13) ; 13) 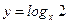 ; ; | 7) 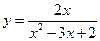 ; 8) ; 8) 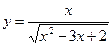 ; 9) ; 9) 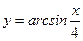 ; 10) ; 10) 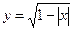 ; 11) ; 11) 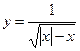 ; 12) ; 12) 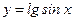 ; 14) ; 14) 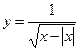 . . |
II. Выяснить четность следующих функций:
1) 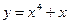 ; 2) ; 2) 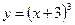 ; 3) ; 3) 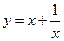 ; 4) ; 4) 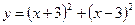 ; 5) ; 5) 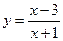 ; 6) ; 6) 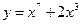 ; ; | 7) 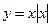 ; 8) ; 8) 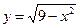 ; 9) ; 9) 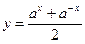 ; 10) ; 10) 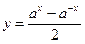 ; 11) ; 11) 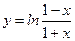 . . |
Ответы:
I. 1) 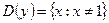 ; 2)
; 2) 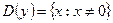 ;
;
3) 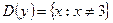 ; 4)
; 4) 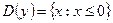 ;
;
5) 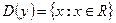 ; 6)
; 6) 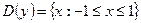 ;
;
7) 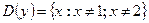 ; 8)
; 8) 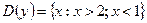 ;
;
9) 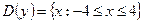 ; 10)
; 10) 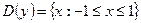 ;
;
11) 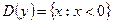 ;
;
12) 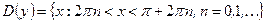 ;
;
13) 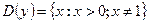 ; 14)
; 14) 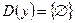 .
.
II. 1), 2), 5) – функция ни четная, ни нечетная;
3), 6), 7), 10), 11) – функция нечетная;
4), 8), 9) – функция четная.
Занятие 2.
Полярная система координат. Построение графиков функций методом сдвига и растяжения вдоль осей
Координат.
Определение.Основные элементы полярной системы координат – полярная ось и полюс. По отношению к ним определяется положение точки на плоскости. Полярные координаты точки 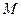 – это пара чисел
– это пара чисел 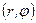 , где
, где 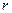 – расстояние от
– расстояние от 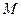 до полюса
до полюса 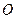 , а
, а 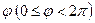 – это угол между полярной осью и
– это угол между полярной осью и 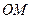 . (см. рис.1).
. (см. рис.1).

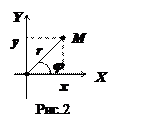
Пусть полярная система координат расположена так, что полюс совпадает с началом декартовой системы координат, а полярная ось – с осью 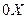 . Пусть точка
. Пусть точка 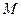 имеет декартовы координаты
имеет декартовы координаты 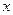 и
и 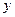 , т.е.
, т.е. 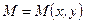 , а полярные –
, а полярные – 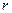 и
и 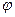 , т.е., с другой стороны,
, т.е., с другой стороны, 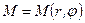 (см. рис.2).
(см. рис.2).
Тогда:
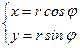 ;
; 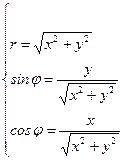
Примеры:
1)Даны декартовы координаты точки 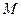 :
: 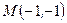 . Найти её полярные координаты, т.е.
. Найти её полярные координаты, т.е. 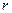 и
и 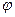 .
.
▲ Имеем: 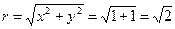 ,
, 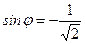 ,
,
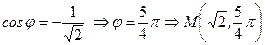 .
.
2)Даны полярные координаты точки 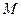 :
: 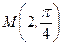 . Найти её декартовы координаты, т.е.
. Найти её декартовы координаты, т.е. 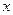 и
и 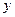 .
.
▲ Имеем: 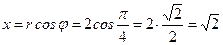 ,
,
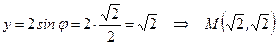 .
.
3)Задать кривые в полярных координатах (при помощи уравнения 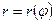 ).
).
а) 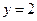 ; б)
; б) 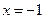 ; в)
; в) 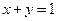 .
.
▲ Подставим в уравнение кривой вместо 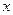 выражение
выражение 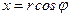 , а вместо
, а вместо 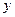 – выражение
– выражение 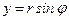 , и выразим
, и выразим 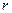 через
через 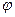 :
:
а) 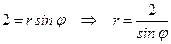 ;
;
б) 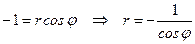 ;
;
в) 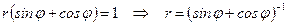 .
.