Графический метод решения задачи линейного

Программирования

Для решения задачи линейного программирования графическим методом выражение базисных переменных через свободные из (3.11) подставим в формулу (3.1), получим линейную функцию, зависящую от двух свободных переменных, то есть, Ф = Г_о + Г₁· х₁ + Г₂· х₂

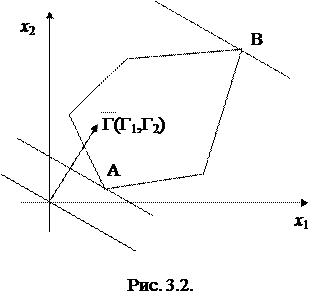В системе координат х₁Ох₂ (рис. 3.2) - это уравнение прямой с угловым коэффициентом - Г₁/Г₂, перпендикулярную вектору-градиенту 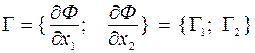, выходящему из начала координат.

Для каждой точки плоскости линейная функция принимает фиксированное значение Ф=Ф_i. При различных значениях Ф получим семейство параллельных прямых – линий уровня.

При x₁ = x₂ = 0 получим Ф_о= Г_о, то есть, при Ф_о = Г_о имеем прямую, проходящую через начало координат. Если эту прямую передвигать параллельно самой себе в положительном направлении вектора Г, то значение линейной функции Ф будет возрастать, а в противоположном направлении – убывать.

Пусть при движении прямой Ф в положительном направлении вектора Г она впервые встретится с многоугольником решений в одной из его вершин, например, в вершине А и принимает значение Ф_А. В этом положении прямая Ф становится опорной, и на этой прямой функция Ф принимает наименьшее из значений, принимаемых на многоугольнике решений, то есть, Ф_min = Ф_А.

При дальнейшем движении в том же (положительном) направлении значение линейной функции продолжает расти и в какой-то момент прямая Ф пройдет через крайнюю точку ОДР, наиболее удаленную от начала координат в направлении перемещения (точка В), которая также является опорной; на ней функция Ф принимает значение Ф_В, которая является наибольшей среди всех значений, принимаемых на многоугольнике решений, то есть, Ф_max = Ф_В.

Таким образом, если число свободных переменных равно 2 (при любом числе базисных) решение ОЗЛП может быть получено простым геометрическим построением на плоскости.

Аналогично, линейная функция трех переменных Ф=Г_о+Г₁·х₁+Г₂·х₂+ Г₃·х₃ принимает постоянное значение на плоскости, перпендикулярной вектору Г(Г₁;Г₂;Г₃). Наименьшее и наибольшее значения этой функции на многограннике решений достигаются в точках пересечения этого многогранника решения с опорными плоскостями, перпендикулярными вектору Г. Опорная плоскость может иметь с многогранником решений либо одну общую точку (вершину многогранника), либо бесконечное множество точек (ребро или грань многогранника).

Итак, если целевая функция задачи линейного программирования ограничена на многограннике решений, то:

1) каждый опорный план (допустимое базисное решение) соответствует угловой точке многогранника решений. Поэтому для решения ОЗЛП необходимо исследовать только угловые точки многогранника решений, т.е. только допустимые базисные решения (опорные планы).

2) существует такая угловая точка многогранника решений, в которой целевая функция достигает своего экстремума;

Идею графического метода решения задачи линейного программирования рассмотрим на конкретном примере.

Пример 3.1.Найти максимальное и минимальное значения

линейной функции Ф = 2·x₁ + 2·x₂

при ограничениях: 3·х₁ – 2·х₂ ≥ -6;

3·x₁ + x₂ ≥ 3;

х₁ ≤ 3.

******************* РЕШЕНИЕ ********************************

Заменив в системе ограничений условно знаки неравенств знаками равенств, получим систему уравнений

3·x₁ – 2·x₂ = – 6 (1) ;

3·x₁ + x₂ = 3 (2);

x₁ = 3 (3).

Построим по этим уравнениям прямые (рис. 3.1.1), затем согласно знакам неравенств выделим соответствующие полуплоскости, которые, пересекаясь, образуют общую часть – треугольник NPS.

Из этого треугольника с учетом условия неотрицательности переменных выделим область допустимых решений (ОДР), представляющую собой четырехугольник MNPQ.

Из начала координат построим вектор - градиент

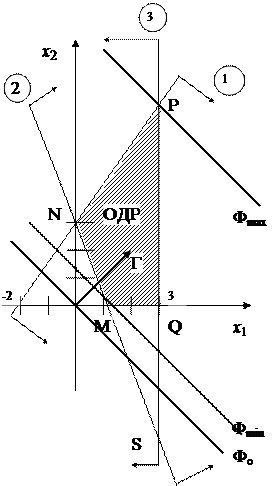
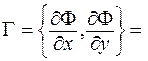{C₁, C₂} = (2; 2).

Затем через начало координат (то есть, при х₁= х₂ = 0) проведем линию уровня - прямую Фо ┴ Г, соответствующую значению целевой функции Ф_о = 0.

Ф_оÏОДР, перемещаем ее в направлении к ОДР. Так как направление перемещения прямой Ф совпадает с положительным направлением вектора Г, то значение целевой функции при этом возрастает.

Рис. 3.1.1

И в точке М (1, 0) прямая Ф впервые встречается с ОДР и становится опорной. В этой точке целевая функция достигает минимального (удовлетворяющего системе ограничений) значения, то есть, minФ = 2×1 + 2×0 = 2.

Двигаем линию уровня Ф дальше в том же направлении (в положительном направлении Г), при этом значение целевой функции продолжает расти. В точке Р(3; 15/2) линия уровня встречается с ОДР в последний раз. В этой точке функция Ф достигает наибольшего значения, (удовлетворяющего системе ограничений), то есть Ф_р= maxФ = 2∙3 + 2∙(15/2) = 21.

Ответ: minФ = 2 при Х_М = (1, 0),

maxФ = 21 при Х_Р = (3; 15/2).

*******************