Задания для подготовки к экзамену
Задания части В (раздел «Алгебра и начала анализа»)
1. Компакт-диск стоит 30 рублей. Какое наибольшее число таких дисков можно будет купить на 250 рублей после понижения цены на 20%?
2. Клиент взял в банке кредит 6000 рублей на год под 15 %. Он должен погашать кредит, внося в банк ежемесячно одинаковую сумму денег, с тем, чтобы через год выплатить всю сумму, взятую в кредит, вместе с процентами. Сколько рублей он должен вносить в банк ежемесячно?
3. 48 выпускников школы собираются учиться в технических вузах. Они составляют 40% от числа выпускников. Сколько в школе выпускников?
4. Мобильный телефон стоил 5000 рублей. Через некоторое время цену на эту модель снизили до 4050 рублей. На сколько процентов была снижена цена?
5. Мебельный салон заключает договоры с производителями мебели. В договорах указывается, какой процент от суммы, вырученной за продажу мебели, поступает в доход мебельного салона. В таблице приведены цены на четыре кресла-качалки.
| Фирма-производитель | Изделие | Цена | Процент от выручки, поступающий в доход салона | Примечания для расчёта процента от выручки |
| «Альфа» | «Агния» | 13500 руб. | 7 % | Изделия ценой до 20000 руб. |
| «Альфа» | «Валерия» | 20500 руб. | 2,5 % | Изделия ценой свыше 20000 руб. |
| «Бета» | «Ева» | 17500 руб. | 3 % | Все изделия |
| «Омикрон» | «Казимира» | 15000 руб. | 6 % | Все изделия |
Определите, продажа какого кресла-качалки наиболее выгодна для салона. В ответ запишите, сколько рублей поступит в доход салона от продажи этого кресла-качалки.
6. В таблице даны тарифы на услуги трех фирм такси. Предполагается поездка длительностью 40 минут. Нужно выбрать фирму, в которой заказ будет стоить дешевле всего. Сколько рублей будет стоить этот заказ?
| Фирма такси | Подача машины | Продолжительность и стоимость минимальной поездки* | Стоимость 1 минуты сверх продолжительности минимальной поездки (в руб.) |
| А | 200 руб. | Нет | |
| Б | Бесплатно | 10 мин. — 200 руб. | |
| В | 150 руб. | 15 мин. — 300 руб. |
*Если поездка продолжается меньше указанного времени, она оплачивается по стоимости минимальной поездки.
7. Пристани A и B расположены на озере, расстояние между ними равно 240 км. Баржа отправилась с постоянной скоростью из A в B. На следующий день после прибытия она отправилась обратно со скоростью на 7 км/ч больше прежней, сделав по пути остановку на 14 часов. В результате она затратила на обратный путь столько же времени, сколько на путь из A в B. Найдите скорость баржи на пути из A в B. Ответ дайте в км/ч.
8. Лодка в 5:00 вышла из пункта А в пункт В, расположенный в 30 км от А. Пробыв в пункте В 2 часа, лодка отправилась назад и вернулась в пункт А в 23:00 того же дня. Определите (в км/ч) скорость течения реки, если известно, что собственная скорость лодки равна 4 км/ч.
9. На рисунке изображены график функции 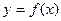 и касательная к нему в точке с абсциссой х0. Найдите значение производной функции
и касательная к нему в точке с абсциссой х0. Найдите значение производной функции 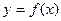 в точке х0.
в точке х0.
а)  б)
б) 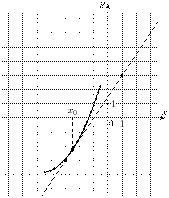 в)
в) 
10. Найдите точку минимума функции: а) 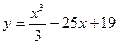 ; б)
; б) 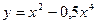 .
.
11. Найдите точку максимума функции: а) 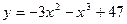 ; б)
; б) 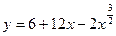 .
.
12. Найдите наименьшее значение функции а) 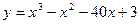 на отрезке [0; 5];
на отрезке [0; 5];
б) 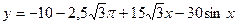 на отрезке
на отрезке 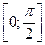 .
.
13. Найдите наибольшее значение функции а) 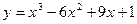 на отрезке [0; 2];
на отрезке [0; 2];
б) 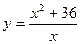 на отрезке [-10; -1].
на отрезке [-10; -1].
14. Вычислите площадь фигуры, ограниченной линиями:
а) 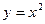 ,
, 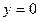 ,
, 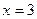 ; б)
; б) 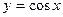 ,
, 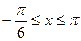 ; в)
; в) 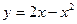 ,
, 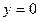 ; г)
; г) 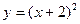 ,
, 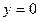 ,
, 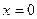 ; д)
; д) 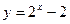 ,
, 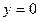 ,
, 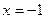 .
.
Задания части В (раздел «Геометрия»)
15. Найдите координаты векторов 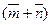 и
и 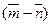 и вычислите угол между ними:
и вычислите угол между ними:
а) 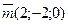 ,
, 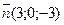 ; б)
; б) 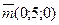 ,
, 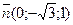 .
.
16. Найдите координаты вектора 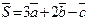 и вычислите его длину, если
и вычислите его длину, если 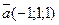 ,
, 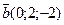 ,
, 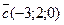 .
.
17. Найдите скалярное произведение векторов: а) 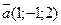 ,
, 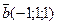 ; б)
; б) 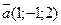 ,
, 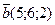 .
.
18. При каком значении n векторы перпендикулярны: а) 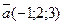 ,
, 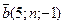 ; б)
; б) 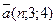 ,
, 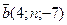 .
.
19. Найдите значение y и z , если векторы 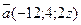 и
и 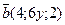 коллинеарны.
коллинеарны.
20. Даны точки А(1;3;0) и В(2;3;-1), а также вектор 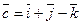 . Найдите координаты векторов
. Найдите координаты векторов 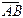 и
и 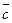 и ответьте на вопрос, коллинеарны ли эти векторы.
и ответьте на вопрос, коллинеарны ли эти векторы.
21. Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 6 и 8 см, боковое ребро равно 5 см. Найдите площадь поверхности и объем призмы.
22. Основанием параллелепипеда является ромб со стороной 1 м и острым углом 60 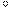 . Боковое ребро параллелепипеда, равное 2 м, составляет с плоскостью основания угол 60
. Боковое ребро параллелепипеда, равное 2 м, составляет с плоскостью основания угол 60 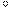 . Найдите объем параллелепипеда.
. Найдите объем параллелепипеда.
23. Сторона основания правильной треугольной призмы равна 10см. Диагональ боковой грани образует с основанием угол 45о. Найдите площадь полной поверхности и объём призмы.
24. Основание прямой призмы - параллелограмм с диагоналями 10 см и 4 см и углом между ними 30о. Меньшая диагональ призмы наклонена к плоскости основания призмы под углом 45о. Найдите объем призмы.
25. Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 2, 4. Диагональ параллелепипеда равна 6. Найдите третье ребро и объем параллелепипеда.
26. Высота правильной четырехугольной пирамиды равна 8 см, а длина апофемы 10 см. Найдите площадь полной поверхности и объем пирамиды.
27. В правильной треугольной пирамиде боковая грань образует с плоскостью основания угол 30о. Найдите площадь полной поверхности и объем пирамиды, если сторона основания 1 см.
28. SABCD – правильная четырехугольная пирамида, боковое ребро которой наклонено к плоскости основания под углом 60о. Найдите объём пирамиды, если сторона основания 10 см.
29. Найдите объём пирамиды, если ее основанием служит прямоугольный треугольник с катетами 6 и 4 дм, а высота пирамиды в два раза больше гипотенузы треугольника, лежащего в основании.
30. Радиус основания цилиндра равен 2, высота равна 3. Найдите площадь боковой поверхности цилиндра и его объём.
31. Осевое сечение цилиндра - квадрат, диагональ которого 1 см. Найдите площадь полной поверхности и объем цилиндра.
32. Найдите объем цилиндра, если длина окружности основания цилиндра равна 4p см, а диагональ осевого сечения образует с плоскостью основания угол 60о.
33. Высота конуса равна 4 см, а диаметр основания — 6 см. Найдите образующую конуса.
34. Площадь основания конуса - 36p см2, а образующая равна составляет с плоскостью основания угол 30о. Найдите площадь поверхности и объём конуса.
35. Осевое сечение конуса – равнобедренный треугольник с основанием 4 см и углом при вершине 60о. Найдите площадь полной поверхности и объем конуса.
36. Площадь большого круга шара равна 3. Найдите площадь поверхности шара.
37. Найдите радиус шара, объем которого равен объему цилиндра высотой 10 см и радиусом 6 см.
Задания части В (раздел «Комбинаторика, статистика и теория вероятностей»)
38. В чемпионате по гимнастике участвуют 50 спортсменок: 17 из России, 22 из США, остальные — из Китая. Порядок, в котором выступают гимнастки, определяется жребием. Найдите вероятность того, что спортсменка, выступающая первой, окажется из Китая.
39. Фабрика выпускает сумки. В среднем на 110 качественных сумок приходится пять сумок со скрытыми дефектами. Найдите вероятность того, что купленная сумка окажется качественной. Результат округлите до сотых.
Задания части С
40. Решите систему неравенств:
a) 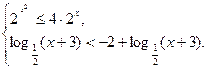
b) 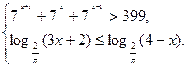
c) 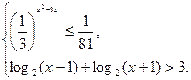
d) 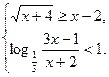
e) 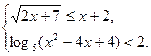
Интернет-ресурсы
1. Открытый банк задач ЕГЭ по математике: http://mathege.ru/.
2. Образовательный портал для подготовки к ЕГЭ в 2012 году: http://reshuege.ru/.
