Элементы теории вероятностей.

Основными понятиями в теории вероятностей являются понятия события и вероятности события. Под событием понимается такой результат эксперимента или наблюдения, который при реализации определенной совокупности условий может произойти или не произойти.

Если событие при заданных условиях может произойти или не произойти, то оно называется случайным. Совокупность условий, при осуществлении которых случайное событие может произойти, либо не произойти, будем называть испытанием или опытом. В том случае, когда событие должно непременно произойти, его называют достоверным, а в том случае, когда оно заведомо не может произойти, - невозможным.

Случайные события обозначаются большими буквами латинского алфавита .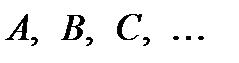

Два события называются несовместными, если появление одного из них исключает появление другого. В противном случае события называются совместными.

Несколько событий в данном опыте образуют полную группу событий, если в результате опыта должно появиться хотя бы одно из них.

В теории вероятностей важную роль играет полная система попарно несовместных событий, то есть такая система событий, что в результате данного испытания непременно произойдет одно и притом только одно событие данной системы.

Два несовместных события, образующих полную группу, называются противоположными.

События называются равновозможными, если условия испытания обеспечивают одинаковую возможность осуществления каждого из них.

Классическое определение вероятности.

Вероятностью события 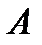называется отношение числа 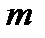элементарных событий, благоприятствующих событию 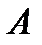, к общему числу 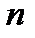равновозможных элементарных событий, то есть

.

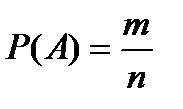Основные свойства вероятности.

1.

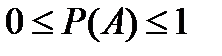
2. Вероятность достоверного события равна 1.

3. Вероятность невозможного события равна 0.

Пример.В урне 3 белых и 9 черных шаров. Из урны наугад вынимают один шар. Какова вероятность того, что вынутый шар окажется черным (событие )?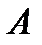

Решение.Имеем 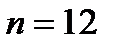, , 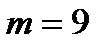и поэтому .

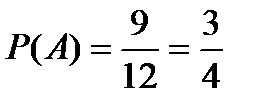Зависимые и независимые события.

Событие 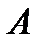называется зависимым от события 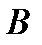, если вероятность события 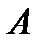меняется в зависимости от того, произошло событие 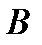или нет. Вероятность события 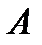, вычисленная при условии, что имело место другое событие 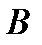, называется условной вероятностью события 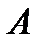и обозначается .

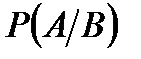Событие 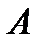называется независимым от события 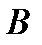, если вероятность события 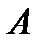не зависит от того, произошло событие 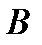или нет. Условие независимости события 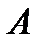от события 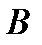можно записать в виде .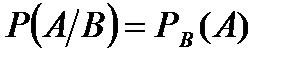