Механическая энергия и её сохранение

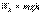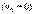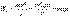Рассмотрим процесс изменения состояния тела, поднятого на высоту h. При этом его потенциальная энергия Тело начало свободно падать . Из кинематики известно, что момент достижения поверхности земли оно будет иметь скорость и кинетическую энергию: Кинетическая энергия тела, упавшего с высоты h, оказалась равной его потенциальной энергии, которую оно имело до начала падения. Следовательно: 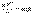На поверхности Земли h=0 и потенциальная энергия 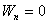, а 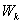-максимальна. В начале падения 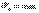, а т.е. потенциальная энергия переходит (превращается) в кинетическую. Таким образом, при падении тела в системе тело-Земля кинетическая энергия возрастает и, следовательно, ее изменение 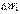равное работе 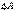, имеет положительный знак, т.е. 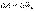Потенциальная энергия - уменьшается, и, следовательно, ее изменение имеет знак минус. Поэтому можем записать: 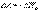Сложив (4.12) и (4.13), получим 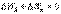или 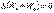Сумма 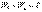представляет собой полную энергию, и, следовательно, , а 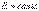Таким образом, энергия замкнутой консервативной системы остается постоянной при всех, происходящих в ней процессах и превращениях. Энергия может переходить из одних видов в другие (механические, тепловые, и т.д.), но общее ее количество остается постоянным. Данное положение называют законом сохранения и превращения энергии.

18. Соударение тел. Абсолютно упругий и неупругий удары.Абсолютно неупругим ударом, называется столкновение двух тел, в результате которого они соединяются вместе и движутся дальше как одно тело. Сталкивающиеся тела деформируются, возникают упругие силы и т.д. Однако если удар неупругий то, в конце концов все эти процессы прекращаются, и в дальнейшем оба тела, соединившись вместе, движутся как единое твёрдое тело.Рассмотрим абс. неупругий удар на примере столкновения двух шаров. Пусть они движутся вдоль прямой, соединяющей их центры, со скоростями v₁ и v₂. В этом случае говорят что удар является центральным. Обозначим за V общую скорость шаров после соударения. Закон сохр. Импульса даёт:m₁v₁+m₂v₂=(m₁+m₂)V V=(m₁v₁+m₂v₂)/(m₁+m₂)Кин. энергии системы до удара и после: K₁=1/2(m₁v₁²+m₂v₂²) K₂=1/2(m₁+m₂)Vпри столкновении двух абсолютно неупругих шаров происходит потеря кин. энергии макроскопического движения, равная половине произведения приведённой массы на квадрат относительной скорости.Абсолютно упругим ударомназывается столкновение тел, в результате которого их внутренние энергии не меняются. Пример: Столкновение бильярдных шаров из слоновой кости, при столкновениях атомных, ядерных частиц. Рассмотрим центральный удар двух шаров, движущ-ся навстречу друг другу:(m₁v₁²)/2+(m₂ v₂²)/2=(m₁u₁²)/2+(m₂ u₂²)/2 и:m₁v₁+m₂v₂=m₁u₁+m₂u₂ u1=[(m₁-m₂)v₁+2m₂v₂]/(m₁ +m₂) 2=[(m₂-m₁)v₂+2m₁v₁]/(m₁+m₂)При столкновении двух одинаковых абсолютно упругих шаров они просто обмениваются скоростями.