Закон сохранения энергии. Внутренняя энергия. Пусть есть мат. точка или частица, которая движется вдоль оси Ох под действием силы
Пусть есть мат. точка или частица, которая движется вдоль оси Ох под действием силы 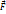 .
.
dA=Fdx=madx=m(dv/dt)dx=m(dx/dt)dv=mvdv; dA=d(mv2/2); T=mv2/2-кинетич.эн.мат.т. dA=-du=d(mv2/2); d(mv2/2+u(x))=0; mv2/2+u(x)=const (1) –Закон сохранения энергии.
Покажем, что ЗСЭ согласуется со 2ым з.Нютона.
E=mv2/2+u(x); dE/dt=m/2*2vdv/dt+du/dx*dx/dt=0; mv(dv/dt)+(du/dx)v=0; F=-du/dx; m(dv/dt)-F=0; F=m(dv/dt).
Силовое поле, в котором движется частица, созд. др. телами. Для того, чтобы поле было постоянным, эти тела должны быть неподвижными. Таким образом, мы получили ЗСЭ в простейшем случае, когда одна частица движется, а все остальные тела, с которыми она взаимодействует – покоятся. Но ЗСЭ мб сформирован и в общем случае, когда имеется ряд движущихся частиц. Если эти частицы образуют замкнутую систему, то для них также справедлив ЗСЭ, согласно которому сумма кинетических энергий всех мат. Точек в отдельности и их взаимная потенциальная энергия не меняются со временем, т.е. E=mv12/2+mv22/2+…+u( 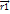 ,
, 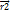 ,…
,…  );
);
Ф. u связана с действующими на каждую точку силами: Fr=-du/dr.
Внутр.эн. Для движения сложной системы можно ввести понятие скорости ее движения как целого, понимая под ней скорость движения центра инерции системы. Это означает, что движение системы можно считать как бы состоящей из 2 движений: движения ее как целого и внутреннего движения, составляющих систему частиц относительно центра инерции. В соответствии с этим энергия системы: E=Mv2/2+Eвнутр., где М-масса всех частиц, входящих в систему, v-скорость центра инерции, а Евнутр включает в себя кинет энерг движ част +их потенц эн взаимод. 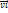 +
+  -скорость i-той частицы(ее собств vi+ скор центра инерц сист v);
-скорость i-той частицы(ее собств vi+ скор центра инерц сист v);
 12.Вращательный момент. Основное уравнение.
12.Вращательный момент. Основное уравнение.
Момент силы 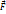 относ неподвижн т.О назыв физ величина, опред вект произвед координат вектора r, проведенного из т.О в т.А прилож силы, на силу
относ неподвижн т.О назыв физ величина, опред вект произвед координат вектора r, проведенного из т.О в т.А прилож силы, на силу 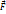 .
. 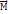 =[
=[  ,
, 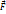 ].
]. 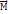 – псевдовектор, его направление совпадает с направлением поступательного движения правого винта при его вращени от
– псевдовектор, его направление совпадает с направлением поступательного движения правого винта при его вращени от  к
к 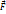 . Модуль момента силы М=FrSin
. Модуль момента силы М=FrSin 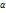 =Fl, где
=Fl, где 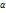 – угол между
– угол между  и
и 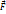 , rSin
, rSin 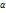 =l – кратчайшее расстояние между линией действия силы и т.О – плечо силы.(рис1)
=l – кратчайшее расстояние между линией действия силы и т.О – плечо силы.(рис1)

 Момент силы относительно неподв оси Z наз скалярная велич М2, равная проекции на эту ось вектора
Момент силы относительно неподв оси Z наз скалярная велич М2, равная проекции на эту ось вектора 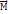 момента силы, опред относ произвольной т.О данной Z. Значение момента Mz не зависит от выбора положения т.О на оси ОZ. Если ОZ совпадает с направлением вектора
момента силы, опред относ произвольной т.О данной Z. Значение момента Mz не зависит от выбора положения т.О на оси ОZ. Если ОZ совпадает с направлением вектора 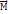 , то момент силы представл в виде вект, совпад с осью
, то момент силы представл в виде вект, совпад с осью 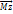 =[
=[  ,
, 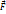 ]z. (рис 2).При повороте тела на бесконечно малый угол d
]z. (рис 2).При повороте тела на бесконечно малый угол d  т. приложения В проходит путь ds=rd
т. приложения В проходит путь ds=rd  . Тогда dA=FSin
. Тогда dA=FSin 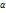 rdU(1). dA=MzdU; Работа при вращ тела идет на увелич его кинет эн.(рис3). dA=dE; dE=d(IZ
rdU(1). dA=MzdU; Работа при вращ тела идет на увелич его кинет эн.(рис3). dA=dE; dE=d(IZ  2/2)=IZ
2/2)=IZ  d
d  . Поскольку dU=
. Поскольку dU=  dF, получ Mz=Iz(d
dF, получ Mz=Iz(d  /dt)=Iz
/dt)=Iz  (2)-уравнение вращ. Движения твердого тела относ подв оси. Если ось Z совпад с главной осью инерц, проход через ценрт масс, то
(2)-уравнение вращ. Движения твердого тела относ подв оси. Если ось Z совпад с главной осью инерц, проход через ценрт масс, то 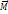 =I*
=I*  (3), I-главный мом инерц тела.
(3), I-главный мом инерц тела.
13.Импульс.Реактивное движение.
При свободном движ мат т.,когда она не взаим с др телами, ее v=const. Напротив, если мат точки взаим друг с др, то скор их меня.тся с течен времени. Изменения скор взаимод част не явл полностью независ, а связ между собой.
Чтобы выяснить, какова эта зависимость, введем понятие замкн системы, под которой будем понимать совокупность мат т., взаимод друг с др и не взаимод с окруж телами.
Для замкн системы сущ ряд велич, свзя со скор и не меняющ со временем. M,q, E/
 =m1
=m1 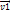 +…+mn
+…+mn 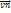 =const-З-н сохр имп. Исходя из ЗСИ скорость 2ух частиц обратно пропорц их массам.
=const-З-н сохр имп. Исходя из ЗСИ скорость 2ух частиц обратно пропорц их массам.
Пусть замкн сист сост из 1ой част.  =m
=m  ; d
; d  /dt=0=m(d
/dt=0=m(d  /dt); m
/dt); m 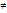 0
0 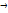 (d
(d  /dt)=0
/dt)=0 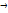 (d
(d  /dt)=const; Незамкнутая система:
/dt)=const; Незамкнутая система:
d  /dt=
/dt= 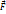 ; d(m
; d(m  )/dt=
)/dt= 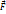 ; m(d
; m(d  /dt)=
/dt)= 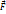 ; m
; m  =
= 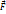 -2ой зак Нюьютона.
-2ой зак Нюьютона.
Реактивное движение. Пусть масса ракеты и ее скорость в опред момент врем: М и 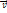 . Пусть в этот момент времени начинают выходить газы со скор
. Пусть в этот момент времени начинают выходить газы со скор 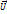 . Через некотор dt масса ракеты уменьш и станет M+dM (dM-отриц), а скор увелич и станет v+dv. Сравнить импульсы системы ракета+газы в момент времени t и dt. Mv=(M+dM)(v+dv)-dM(v-u);
. Через некотор dt масса ракеты уменьш и станет M+dM (dM-отриц), а скор увелич и станет v+dv. Сравнить импульсы системы ракета+газы в момент времени t и dt. Mv=(M+dM)(v+dv)-dM(v-u); Mv=Mv+Mdv+dMv+dMdv(беск мало)-dMv+udM; mdv+udM=0; dM/m=-dv/u; 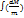 =-v/u; d(
=-v/u; d( 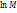 )=-d(v/u); lnM+v/u=const;
)=-d(v/u); lnM+v/u=const;
t=0; M=M0; v=0; lnM0+0=const; lnM+v/u=lnM0; ln(M/M0)=-v/u; v=uln(M0/M);
