Расчет тонкостенного стержня с открытым разветвленным контуром поперечного сечения
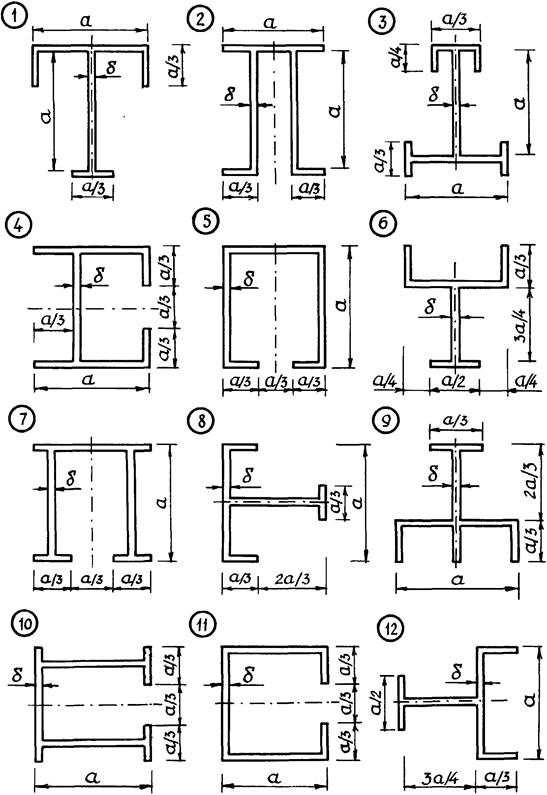
По данным таблицы 8 принять схему загружения тонкостенного стержня, его опорные закрепления и размеры поперечного сечения. Выполнить поверочный расчет тонкостенного стержня на прочность.
Содержание и порядок расчета.
1.Определить положение центра тяжести поперечного сечения, главных центральных осей инерции 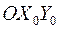 и построить эпюры координат
и построить эпюры координат 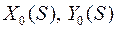 .
.
2.Построить эпюру секториальной площади 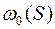 с полюсом в центре тяжести поперечного сечения. Вычислить главные центральные моменты инерции
с полюсом в центре тяжести поперечного сечения. Вычислить главные центральные моменты инерции 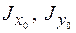 и линейно-секториальные моменты
и линейно-секториальные моменты 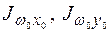 .
.
3.Определить координаты центра изгиба поперечного сечения, построить эпюру главной секториальной площади 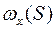 с полюсом в центре изгиба и началом отсчета в главной точке и проверить правильность определения положения центра изгиба.
с полюсом в центре изгиба и началом отсчета в главной точке и проверить правильность определения положения центра изгиба.
4.Вычислить главный секториальный момент инерции 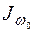 и изгибно-крутильную характеристику
и изгибно-крутильную характеристику 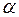 , приняв при этом
, приняв при этом 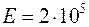 МПа,
МПа, 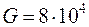 МПа.
МПа.
5.Определить внутренние силовые факторы в поперечных сечениях стержня и построить их эпюры: от поперечного изгиба 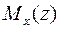 ,
, 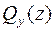 ; от стесненного кручения
; от стесненного кручения 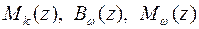 . При этом можно использовать табличные данные эпюр изгибающих моментов и перерезывающих сил от частного вида нагрузок и опорных закреплений стержней и таблицы функций углов закручивания
. При этом можно использовать табличные данные эпюр изгибающих моментов и перерезывающих сил от частного вида нагрузок и опорных закреплений стержней и таблицы функций углов закручивания 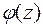 при стесненном кручении.
при стесненном кручении.
6.Установить опасное, с точки зрения прочности, сечение, в котором построить эпюры нормальных 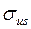 и касательных
и касательных 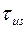 напряжений при поперечном изгибе, нормальных
напряжений при поперечном изгибе, нормальных 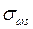 и касательных
и касательных 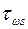 при стесненном кручении, а также суммарные эпюры
при стесненном кручении, а также суммарные эпюры 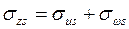 ;
; 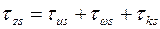 .
.
7.В опасном сечении определить ряд (две, три) расчетных точек, в которых проверить прочность, используя критерии прочности по третьей или четвертой теориям прочности и сделать заключение о рациональности заданного поперечного сечения стержня.
8.По заданию преподавателя выполнить поверочный расчет одного из этапов решения с использованием персональных ЭВМ.
Литература
1. Терегулов И.Г. Сопротивление материалов и основы теории упругости и пластичности.- М.: Высшая школа, 1984, стр. 325-338.
2. Смирнов А.Ф., Александров А.В. и др. Сопротивление материалов.- М.: Высшая школа, 1975, стр.311-342.
3. Александров А.В. и др. Сборник задач по сопротив-лению материалов.- М.: Стройиздат, 1977, стр.216-238.
Схема загружения
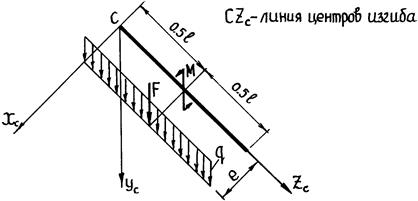
таблица 8
| а | б | в | г | |||||
| Опасное закрепление | 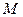 , (кНм) , (кНм) | 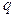 , (кН/м) , (кН/м) | 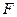 , (кН) , (кН) | 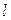 , (м) , (м) | 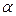 , (см) , (см) | 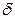 , (см) , (см) | 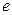 , (см) , (см) | |
 | 9.0 | 3.0 | - | 4.5 | 0.8 | 2.5 | ||
 | - | 1.0 | 60.0 | 6.0 | 0.5 | 5.0 | ||
 | - | 2.0 | 10.0 | 5.0 | 4.0 | |||
 | - | 3.0 | 8.0 | 5.5 | 1.2 | 5.0 | ||
 | 9.0 | 4.0 | - | 4.0 | 6.0 | |||
 | - | 3.5 | 90.0 | 4.5 | а* | |||
 | 7.0 | 6.0 | - | 5.0 | 3.0 | |||
 | 3.0 | - | 3.5 | 1.1 | 4.0 | |||
 | - | 3.0 | 70.0 | 5.0 | 0.8 | 5.0 | ||
 | 8.0 | 4.0 | - | 4.0 | 1.2 | 6.0 |

4. Бычков Д.В. Расчет балочных и рамных систем из тонкостенных элементов,- М.: Стройиздат, 1948.- стр.186-201.
ЗАДАНИЕ № 8
ИЗГИБ Плиты
Для прямоугольной плиты, шарнирно опертой по всему контуру, загруженной равномерно распределенной нагрузкой 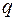 при заданных размерах и приведенных характеристиках материала (таблица 9) методом Навье:
при заданных размерах и приведенных характеристиках материала (таблица 9) методом Навье:
1.Получить аналитические соотношения для вычисления погонных внутренних силовых факторов 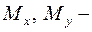 изгибающих моментов,
изгибающих моментов, 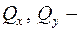 перерезывающих сил,
перерезывающих сил, 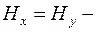 крутящих моментов, реакций –
крутящих моментов, реакций – 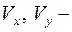 распределенных по контуру,
распределенных по контуру, 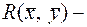 угловых. Здесь
угловых. Здесь 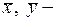 координаты углов плиты.
координаты углов плиты.
2.Построить алгоритм вычисления внутренних силовых факторов или реакций, заданных шифром и выполнить тестовый пример расчета. При вычислении коэффициентов для членов ряда принять m = 1,3,5; n = 1,3,5. В тестовом примере вычислить в режиме ручного счета максимальные величины заданного силового фактора.
3.Проверить правильность вычисления тестового примера с использованием персональной ЭВМ.
4.При удовлетворительной степени точности ручного счета задать шаг сетки ( 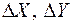 ) и вычислить, используя ЭВМ, все внутренние силовые факторы и реакции в узловых точках сетки и построить эпюры
) и вычислить, используя ЭВМ, все внутренние силовые факторы и реакции в узловых точках сетки и построить эпюры 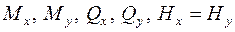 ,
, 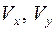 и
и 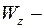 прогиб плиты.
прогиб плиты.
Расчетная схема плИты
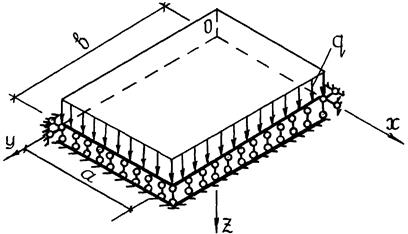
таблица 9
| а | б | в | г | |||||
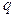 , (кН/м2) , (кН/м2) | 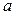 , (м) , (м) | 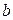 , (м) , (м) | 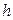 , (м) , (м) | алгоритм | 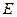 , (МПа) , (МПа) | 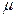 | 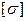 , (МПа) , (МПа) | |
| 4.2 | 6.0 | 0.10 | 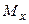 | 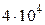 | 0.25 | |||
| 3.0 | 4.2 | 0.08 | 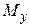 | 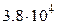 | 0.20 | |||
| 4.8 | 5.4 | 0.12 | 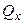 | 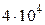 | 0.22 | |||
| 3.6 | 4.2 | 0.08 | 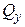 | 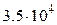 | 0.24 | |||
| 6.0 | 5.4 | 0.10 | 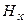 | 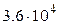 | 0.21 | |||
| 5.4 | 4.2 | 0.08 | 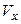 | 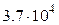 | 0.22 | |||
| 4.8 | 3.6 | 0.12 | 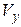 | 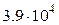 | 0.23 | |||
| 3.6 | 5.4 | 0.12 | 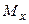 | 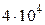 | 0.22 | |||
| 3.0 | 3.6 | 0.12 | 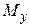 | 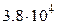 | 0.21 | |||
| 6.0 | 4.8 | 0.10 | 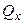 | 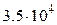 | 0.20 |
5.В узловой точке, где силовые факторы отличны от нуля, построить эпюры изменения напряжений по толщине плиты (по координате z).
Литература
1. Терегулов И.Г. Сопротивление материалов и основы теории упругости и пластичности.- II.: Высшая школа, 1984, стр. 363-400.
2. Александров А.В., Потапов В.Д. Основы теории упругости и пластичности.- М.: Высшая школа, 1990, стр.146-174.
СБОРНИК ЗАДАНИЙ
к расчетно-графическим работам по курсу
«Сопротивление материалов с основами теории
упругости и пластичности»
Под общей редакцией Каюмова Р.А.,Страхова Д.Е.
Редактор
Подписано в печать «__» ______ Бесплатно Формат 60х84/16
Заказ ________ Печать офсетная Усл.печ.л.2,5
Тираж 400 экз. Бумага тид.№2 Уч.-изд.л.2.5
 Адрес института и офсетной лаборатории:
Адрес института и офсетной лаборатории:
420043,Казань, Зеленая,1
