Задания для выполнения отмечены желтым цветом

Теория статистики

Практическое занятие (продолжительность 4 часа)

Внимательно прочитать теорию, только после этого приступать к практическим заданиям

Задания для выполнения отмечены желтым цветом

1. Понятие вероятности.Рассматривается опыт, в результате которого может произойти событие А (исход опыта), произойдет или не произойдет указанное событие в действительности заранее достоверно неизвестно.

Примеры подобного опыта:

1. Бросание монеты, событие А – выпадение орла (герба).

2. Изделие находится в работе, событие А – изделие выйдет из строя на заданном интервале времени.

3. На удачу выбирается день в календаре, событие А – выбранный день оказался воскресеньем.

В теории вероятностей каждому элементарному событию А ставится в соответствие числовая мера возможности его наступления ­ – вероятность события А. Обозначается: Р(А).

Вся теория вероятности базируется на предположении о постоянстве вероятностей, т.е. стационарности рассматриваемых систем на заданном временном интервале и в заданных условиях.

Классическое определение вероятности. Данное определение вероятности основано на симметрии множества возможных исходов опыта.

Предположим, что у опыта имеется N равновозможных исходов, при этом из них m соответствуют наступлению события А, тогда вероятность события А равна отношению m/N, т.е.

P(A)=m/N.

Рассмотрим примеры:

1. Бросание монеты, событие А – выпадение орла (герба). Всего равновозможных исходов два, т.е. N=2 – выпадение орла (герба) и выпадение решки (цифры). Выпадению герба из двух данных исходов соответствует лишь один исход, т.е. m=1. Таким образом, вероятность выпадения герба Р=1/2.

2. Бросание игрального кубика, имеющего 6 граней. Вероятность выпадения цифры 1 – P=1/6. Вероятность выпадения четной цифры P=1/2, так как из 6 равновозможных исходов (N=6) выпадению четной цифры соответствуют три: 2, 4, 6, т.е. m=3. P=3/6=1/2.

2. Случайные величины и их описание.Величина, которая в результате опыта может принимать различные значения в зависимости от случая называется случайной величиной (сокращенно СВ). Другое название случайных величин – случайные числа (СЧ).

Законом распределения случайной величины называется соответствие между возможными значениями СВ и вероятностями их наступления.

Случайная величина X является дискретной, если она может принимать одно из значений на конечном или бесконечном дискретном множестве x₁, x₂, x₃,...

Одним из возможных вариантов представления закона распределения дискретной СВ является ряд распределения – таблица, в которой для возможных значений перечислены соответствующие им вероятности:

X1	X2	X3	X4	....	XN
P1	P2	P3	P4		PN

Так как случайная величина обязательно принимает одно из перечисленных значений, то сумма вероятностей ряда распределения равна 1 т.е. .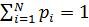

Непрерывная случайная величина – СВ возможные значения которой непрерывно заполняют некоторую область.

Примеры непрерывной СВ: температура воздуха, рост наугад выбранного человека, скорость автомобиля и т.п.

Очевидно, что для непрерывной СВ невозможно построить ряд распределения, так как число возможных значений бесконечно.

Наиболее универсальной формой закона распределения является функция распределения, называемая так же интегральный закон распределения.

Функция распределения численно равна вероятности того, что случайная величина примет значение меньше x, что можно записать формулой:

.

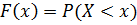F(x) – неубывающая функция, так как с ростом x вероятность того, что X примет значение меньшее, чем x не может возрастать.

Несложно также понять, что 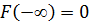и .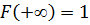

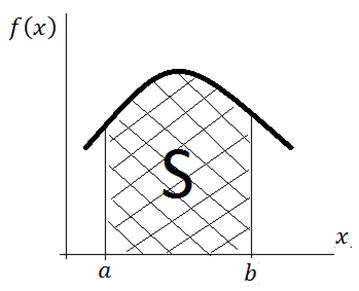
Вероятность попадания случайной величины на заданный интервал (a, b) определяется формулой:

.

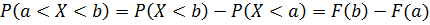Плотность распределения или дифференциальный закон распределения случайной величины определяется формулой:

.

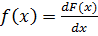Вероятность попадания случайной величины в заданный интервал:

,

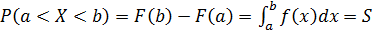S – это площадь заштрихованной области на рисунке.