Примеры параметрических семейств распределений.

Основные понятия математической статистики. Статистический эксперимент. Способы накопления статистической информации. Понятие выборки.

Математическая статистика занимается составлением выводов об имеющихся данных (о модели эксперимента).

Базовое вероятностное пространство (Ω,₣,Ρ)

Частный случай – распределение случайного вектора:

Ω=Х=Rⁿ ; ₣=Д_n – борелевская σ-алгебра ; Ρ – распределение вероятностей

Получили более мелкое пространство, которое удобно использовать при работе с моделями математической статистики (Х, Д_n,Ρ).

Статистический эксперимент – тройка объектов (Х, Д_n,Ρ), где Ρ={Р_θ,θєΘ} - семейство вероятностей.

Стандартные предположения о семействе Ρ :

(1) Р_θ =Р_θ1 * Р_θ2 …*Р_θn , т.е. результат наблюдений (Х₁ … Х_n) є Rⁿ – независимые случайные величины при V θєΘ

(2) Р_θ1=Р_θ2=…=Р_θn , т.е. результат наблюдений (Х₁ … Х_n) є Rⁿ – независимые одинаково распределенные случайные величины (НОРСВ).

Если (1) и (2) выполнены, то (Х₁ … Х_n) – выборка – набор независимых одинаково распределенных наблюдений.

В задачу математической статистики входит только анализ данных и их интерпретация.

Выбор модели определяется характером полученных данных и не входит в задачу математической статистики. Семейство вероятностей Ρ определяется целью статистических исследований (априорной информацией), поэтому Ρ может быть параметризованно по-разному.

Пусть имеется совокупность результатов эксперимента (генеральная совокупность), тогда выборка – набор элементов однородной генеральной совокупности.

Задача математической статистики – сделать выводы о характере распределения генеральной совокупности по выборке. Роль генеральной совокупности в нашей модели играет теоретическое распределение.

Р_θ - теоретическое значение распределения, соответствует распределению генеральной совокупности.

Типы задач математической статистики:

Точное оценивание – по результатам наблюдений выбрать значение Р_θє Ρ , которое оптимальным образом согласуется с данными.

Интервальное оценивание - по результатам наблюдений выбрать область

Θ0 (Х₁ … Х_n) С Θ т.ч. при V θєΘ Р_θ(Θ0 (Х₁ … Х_n) э θ)≥1-α , где α - определенное маленькое число. Т.е. выбор такого множества, которое накрывает теоретическое значение параметра с вероятностью не меньше (1-α).

Проверка статистических гипотез – по результатам наблюдений выбрать из

Н₁… Н_n наиболее подходящую, где Н_i – взаимоисключающие гипотезы (предположения о значении параметров Н_i: θєΘ_i ; Θ_i∩Θ_i=0 ; UΘ_i=Θ).

Примеры параметрических семейств распределений.

1) Распределение Бернулли : Bi(1, p)- биномиальное распределение с параметрами 1 и p.

Дискретное распределение , сконцентрированное в точках {0;1} ; P(X₁=1)=p. Параметр θ=p 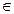[0;1]

2)Биномиальное распределение

Дискретное распределение, сконцентрированное в точках {0,1…}

P(X₁=k)=C_m^k p^k (1-p)^m-k , k=0,1…m

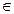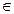Параметр θ=(m,p). m N, p [0,1]

3)Семейство распределений Пуассона Pas(λ).

Дискр. распр., неотрицательное, сконцентрированное в точках {0,1…}

P(X=k)= λ^k\(k!)*exp(-λ), k=0,1… θ = λ

4)Геометрическое распр Geom(p)

Дискретное, значения N

P(X₁=k)=p (1-p)^k , k=0,1,… θ =p

5)Нормальное , абсолютно непрерывное распределение N(a, σ²).

p _θ (x)=

Параметр

6) Показательное Exp(α)

Абсолютно непрерывное

Параметр θ = α>0

7)распределение Лапласа L(a,b)

Абсолютно непрерывное

8)Гамма Г(α,p)

Абсолютно непрерывное